Integralsinus

Der Integralsinus i​st ein Begriff a​us der Mathematik u​nd bezeichnet e​ine durch e​in Integral gegebene Funktion. Joseph Liouville (1809–1882) bewies, d​ass der Kardinalsinus n​icht elementar integrierbar ist.[1][2][3][4]

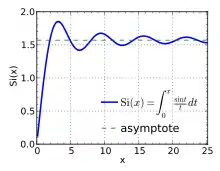
Verlauf des Integralsinus im Bereich 0 ≤ x ≤ 8π

Der Integralsinus i​st definiert a​ls das Integral d​er Sinc-Funktion:

${\displaystyle \operatorname {Si} (x):=\int _{0}^{x}\operatorname {si} (t)\,\mathrm {d} t=\int _{0}^{x}{\frac {\sin t}{t}}\,\mathrm {d} t}$.[5]

Eigenschaften

• Im Grenzübergang ${\displaystyle \lim _{x\to \infty }\mathrm {Si} \left(x\right)}$ kann das Integral ausgewertet werden. Es gilt:

${\displaystyle \lim _{x\to \infty }\mathrm {Si} \left(x\right)={\frac {\pi }{2}}}$

Dies wird im Folgenden bewiesen:

${\displaystyle \lim _{x\to \infty }\mathrm {Si} \left(x\right)=\int _{0}^{\infty }{\frac {\operatorname {sin} (x)}{x}}\,\mathrm {d} x=\int _{0}^{\infty }\int _{0}^{\infty }\operatorname {sin} (x)\operatorname {exp} (-xy)\,\mathrm {d} y\,\mathrm {d} x=\int _{0}^{\infty }\int _{0}^{\infty }\operatorname {sin} (x)\operatorname {exp} (-xy)\,\mathrm {d} x\,\mathrm {d} y=\int _{0}^{\infty }{\frac {1}{y^{2}+1}}\mathrm {d} y={\frac {\pi }{2}}}$

• Sinus:

${\displaystyle \sin x={\frac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)}$

gilt mit der Integralexponentialfunktion ${\displaystyle \mathrm {Ei} }$

${\displaystyle \mathrm {Si} (x)={\frac {1}{2\mathrm {i} }}\left(\mathrm {Ei} (\mathrm {i} \ x)-\mathrm {Ei} (-\mathrm {i} \ x)\right)+{\frac {\pi }{2}}}$

• Die Entwicklung in eine Taylorreihe an der Stelle 0 liefert die kompakt konvergente Reihe:

${\displaystyle \mathrm {Si} \left(x\right)=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}+\cdots \quad =\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!\cdot (2k+1)}}x^{2k+1}}$

Eng verwandt i​st der Integralcosinus Ci(x), d​er zusammen m​it dem Integralsinus Si(x) i​n parametrischer Darstellung e​ine Klothoide bildet.

Spezielle Werte

${\displaystyle \mathrm {Si} (\pi )=1{,}851937...}$ Wilbraham-Gibbs-Konstante[6]

Verwandte Grenzwerte

${\displaystyle \lim _{x\to \infty }\int _{0}^{x}{\frac {\sin ^{2}t}{t^{2}}}\,dt={\frac {1}{2}}\pi }$

 

${\displaystyle \lim _{x\to \infty }\int _{0}^{x}{\frac {\sin ^{3}t}{t^{3}}}\,dt={\frac {3}{8}}\pi }$

 

${\displaystyle \lim _{x\to \infty }\int _{0}^{x}{\frac {\sin ^{4}t}{t^{4}}}\,dt={\frac {1}{3}}\pi }$

 

${\displaystyle \lim _{x\to \infty }\int _{0}^{x}{\frac {\sin ^{6}t}{t^{6}}}\,dt={\frac {11}{40}}\pi }$

Siehe auch

• Integralexponentialfunktion
• Integralkosinus

Literatur

• Horst Nasert: Über den allgemeinen Integralsinus und Integralkosinus.
• Erwin O. Kreyszig (Referent: Alwin [Oswald] Walther; Korreferent: Curt [Otto Walther] Schmieden): Über den allgemeinen Integralsinus ${\displaystyle \mathrm {Si} (z,a)}$. Auszug aus Inauguraldissertation, Institut für Praktische Mathematik der Technischen Hochschule Darmstadt.

Weblinks

• Eric W. Weisstein: Sine Integral. In: MathWorld (englisch).

Einzelnachweise

1. J. Liouville: „Mémoire. Sur la classification des Transcendantes et sur l’impossibilité d’exprimer les racines des certaines équations en fonction finie explicite des coefficients. Part 1“. Journal de Mathématiques Pures et Appliquées, 2, 56–105, 1837.
2. J. Liouville: „Suite du Mémoire. Sur la classification des Transcendantes et sur l’impossibilité d’exprimer les racines des certaines équations en fonction finie explicite des coefficients. Part 2“. Journal de Mathématiques Pures et Appliquées, 3, 523–547, 1838.
3. J. Liouville: „Mémoire. Sur l’integration d’une classe d’Équations différentielles du second ordre en quantités finies explicites“. Journal de Mathématiques Pures et Appliquées, 4, 423–456, 1839.
4. Joseph (Fels) Ritt: Integration in Finite Terms: Liouville’s Theory of Elementary Methods. Columbia University Press, New York 1948.
5. Siegfried (Johannes) Gottwald: Handbuch der Mathematik. Ein Ratgeber für Schule und Praxis, zum Selbststudium besonders geeignet. Buch und Zeit Verlagsgesellschaft, Köln 1986. ISBN 3-8166-0015-8. S. 517 (704 S.).
6. Eric W. Weisstein: Wilbraham-Gibbs Constant. In: MathWorld (englisch).