Zweidimensionale Kernspinresonanzspektroskopie

Unter zweidimensionaler Kernspinresonanzspektroskopie (2D-NMR) versteht man Kernspinresonanzspektroskopieverfahren, bei denen die Intensitäten in Abhängigkeit von zwei Frequenzachsen aufgezeichnet werden, generiert also dreidimensionale Diagramme.[1] Zweidimensionale NMR-Spektren liefern mehr Informationen über ein Molekül als eindimensionale NMR-Spektren und sind deshalb besonders nützlich bei der Bestimmung der Struktur eines Moleküls, insbesondere für Moleküle deren Struktur zu kompliziert ist, um sie mit eindimensionalen NMR zu untersuchen.

Beschreibung

Das Verfahren beruht darauf eine Reihe an Spektren aufzunehmen und währenddessen einen Pulsparameter kontinuierlich in seiner Dauer zu verändern, wodurch sich Phase und Intensität der Spektren systematisch ändern. Durch erneute Fouriertransformation der einzelnen Punkte der Spektren entlang dieser Zeitachse wird aus den eindimensionalen Spektren ein zweidimensionales erhalten.

Werden dabei auf der einen Frequenzachse chemische Verschiebungen aufgetragen und auf der anderen Kopplungskonstanten, so spricht man von zweidimensionalen J-aufgelösten NMR-Spektren.[1]

Die Entwicklung machte jedoch bei zwei Dimensionen nicht halt. Durch Variation weiterer Parameter können höherdimensionale Spektren erhalten werden. Die benötigte Spektrenzahl und damit Messzeit steigt dabei exponentiell an. Inzwischen werden auch dreidimensionale Experimente (3D-NMR) mit drei Frequenzachsen fast routinemäßig durchgeführt, wobei auf jeder Achse die Resonanzen eines anderen Kernes aufgetragen sein können Zum Beispiel ¹H, ¹³C, ¹⁵N oder ³¹P. Es können jedoch auch auf zwei Achsen ¹H-Resonanzen und nur auf der dritten ein Heterokern abgetragen werden.[2]

Die zweidimensionale Kernresonanzspektroskopie hat gegenüber eindimensionalen Methoden mehrere Vorteile:[3]

Durch die Aufteilung auf zwei Dimensionen kann man auch komplizierte Spektren auflösen die in einer Dimension durch starke Überlagerungen nicht mehr interpretierbar sind.
Man erhält die gesamte Information über alle Gruppen des Moleküls auf einmal.
Man kann auf zwei Dimensionen verschiedene physikalische Wechselwirkungen auswählen, nach denen man separieren will. Dadurch sind verschiedene Verfahren der 2D-NMR möglich.
Weiterhin kann man Mehrquantenübergänge, die in erster Näherung spinverboten sind, in der zweidimensionalen NMR-Spektroskopie beobachten.

Ausführung

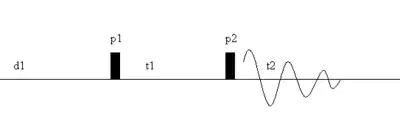
Das Basisexperiment der 2D-NMR lässt sich vom Ablauf her schematisch in vier Zeitabschnitte einteilen die Präparationsphase, die Evolutionsphase, die Mischphase und die Detektionsphase. Während der Detektionsphase werden die Signale, wie im konventionellen eindimensionalen Fall, in äquidistanten Abständen Δt₂ detektiert, digitalisiert und abgespeichert. In der Präparationsphase wird longitudinale Polarisation aufgebaut. Sie endet meist mit einem 90°-Puls, der Quermagnetisierung erzeugt. Während der Evolutionsphase mit der variablen Zeitdauer t₁ entwickeln sich Kohärenzen unter dem Einfluss verschiedener Faktoren (z. B. Larmorpräzession, Spin-Spin-Kopplung), die in der Mischperiode, die jedoch nicht immer notwendig ist, miteinander gekoppelt und in detektierbare Transversalmagnetisierung umgewandelt werden. Die Evolutionszeit t₁ wird von Experiment zu Experiment um einen festen Wert dt1 stufenweise erhöht. Der zu jedem Δt₁-Wert gehörige FID (free induction decay) wird getrennt abgespeichert. Man erhält also eine zweidimensionale Matrix, die jedem Paar (t₁,t₂) eine Signalamplitude S(t₁,t₂) zuordnet. Eine zweidimensionale Fouriertransformation führt dann das Zeitsignal S(t₁,t₂) in das Frequenzsignal S(ω₁,ω₂) über.[3]

S(\omega _{1},\omega _{2})=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }S(t_{1},t_{2})e^{-i\omega t_{1}}e^{-i\omega t_{2}}dt_{2}dt_{1}

Alle FIDs werden wie gewöhnlich als Funktion von t₂ transformiert. Die daraus entstehende neue Datenmatrix enthält nun nach t₁ geordnet in den Reihen (der ω₂-Richtung) die NMR-Spektren. Als nächstes wird noch einmal in t₁-Richtung transformiert. Die Darstellung erfolgt in Form eines 3D-Diagramms (en: stacked plot) oder als Konturliniendiagramm in einem quadratischen Diagramm, dessen Achsen die üblichen Frequenzskalen darstellen.[3]

Geschichte

Nach einem Vorschlag von Jean Jeener aus dem Jahr 1971 wurden Mehrpulsexperimente mit einer systematisch variierten Wartezeit zwischen zwei Pulsen entwickelt, die nach Fourier-Transformation über zwei Zeitbereiche zu zweidimensionalen Spektren führten.[4] In den siebziger Jahren waren Richard R. Ernst und seine Mitarbeiter entscheidend an der Entwicklung der 2D-NMR beteiligt. Im Jahre 1991 erhielt er den Nobelpreis für Chemie.[3][5] Durch seine und die Arbeiten von R. Freemann wurde die 2D-NMR praktisch realisierbar.[2] Kurt Wüthrich und andere bauten diese 2D- und Multi-Dimensions-NMR zu einer bedeutenden Analysetechnik der Biochemie aus, insbesondere zur Strukturanalyse von Biopolymeren wie Proteinen. Wüthrich bekam für diese Arbeiten 2002 den Nobelpreis in Chemie.[6]

Verfahren zweidimensionaler NMR-Spektroskopie

Durch Auswahl der Spektren zum Beispiel durch Art und Auswahl der zeitlichen Abfolge der Impulse und Berechnungsverfahren sind verschiedene Varianten der 2D-NMR möglich.[7] Wenn man alle Varianten mitrechnet, gibt es inzwischen mehrere hundert verschiedene Arten der 2D-NMR-Spektroskopie. Für biochemische Zwecke spielen jedoch nur wenige eine Rolle.[3] Bei den in der Praxis wichtigsten Verfahren sind zweimal ¹H- oder ¹H- und ¹³C-chemische Verschiebungen miteinander verknüpft. Die zweidimensionalen Verfahren setzen eine Kopplung von Kerndipolen voraus. Dabei muss es sich nicht unbedingt um eine skalare Kopplung handeln Die Wechselwirkung kann wie beim Kern-Overhauser-Effekt auch dipolarer Natur sein, das heißt, sie erfolgt durch den Raum.[2] Häufig verwendete Verfahren sind:

COSY (engl. correlation spectroscopy): Zweidimensionale Methode, bei der gleichartige Kerne (¹H) (homonukleare COSY) oder verschiedenartige Kerne (heteronukleare COSY) über ihre skalaren Kopplungen miteinander korreliert werden. COSY-Spektren sind symmetrisch bezüglich der Diagonalen. Mit COSY können komplizierte Kopplungsmuster räumlich entzerrt werden.

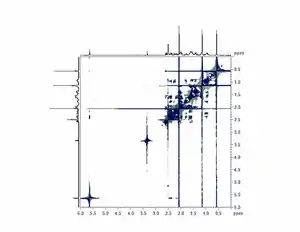
Im Standard-COSY bestehen die Vorbereitungs- (p1) und die Mischperioden (p2) jeweils aus einem einzigen 90°-Puls, der durch die Evolutionszeit t1 getrennt ist. Das Resonanzsignal aus der Probe wird während der Erfassungsperiode über einen Zeitraum von t2 gelesen.

¹H COSY Spektrum von Progesteron

DOSY (engl. diffusion ordered spectroscopy): Verfahren, bei dem mittels Feldgradienten-NMR Moleküle mit unterschiedlichem Diffusionsverhalten NMR-spektroskopisch getrennt erfasst werden können.

TOCSY (engl. total correlated spectroscopy): Zweidimensionale Methode, bei der gleichartige Kerne (¹H) über ihre skalaren Kopplungen miteinander korreliert werden. TOCSY-Spektren sind wie COSY-Spektren symmetrisch bezüglich der Diagonalen. Zusätzlich zu den im COSY detektierten Signalen erscheinen im TOCSY Korrelationen zwischen dem Startkern und sämtlichen indirekt über mehrere Kopplungen mit ihm verbundenen Kernen (Spinsystem). Das TOCSY-Experiment ist vor allem bei der Strukturaufklärung hochmolekularer Substanzen mit räumlich begrenzten Spinsystemen, wie etwa Polysacchariden oder Peptiden, sehr nützlich.

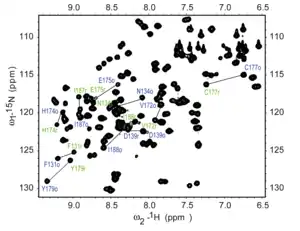
HSQC (engl. heteronuclear single quantum coherence): Zweidimensionale Methode, bei der chemische Verschiebungen unterschiedlicher miteinander skalar koppelnder Nuklide korreliert werden. Die HSQC-Spektren sind häufig recht übersichtlich, da gewöhnlich nur Signale von direkt aneinander gebundenen Atomen erscheinen. Typische Beispiele sind ¹H,¹³C- und ¹H,¹⁵N-Korrelationen.

¹H–¹⁵N HSQC Spektrum eines Fragmentes des Proteins NleG3-2.

HMBC (engl. heteronuclear multiple bond correlation): Zweidimensionale Methode, bei der chemische Verschiebungen unterschiedlicher miteinander skalar koppelnder Nuklide korreliert werden. Im Gegensatz zum HSQC werden im HMBC Korrelationen über mehrere Bindungen angezeigt. Typisch sind vor allem ¹H,¹³C-Korrelationen.

NOESY (engl. nuclear overhauser enhancement and exchange spectroscopy): Zweidimensionale Methode, mit der Korrelationen über den Kern-Overhauser-Effekt (NOE) anstatt über skalare Kopplungen detektiert werden. Mit dieser Methode können räumlich benachbarte Kerne erkannt werden wenn sie nicht skalar miteinander koppeln. Es gibt sowohl homo- als auch heteronukleare Versionen. Dieses Verfahren wird häufig in der Strukturaufklärung eingesetzt.

Weblinks

Commons: Zweidimensionale Kernspinresonanzspektroskopie – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

Matthias Otto: Analytische Chemie. John Wiley & Sons, 2011, ISBN 3-527-32881-5, S. 270 (eingeschränkte Vorschau in der Google-Buchsuche).
Horst Friebolin: Ein- und zweidimensionale NMR-Spektroskopie Eine Einführung. John Wiley & Sons, 2013, ISBN 978-3-527-33492-6, S. 423 (eingeschränkte Vorschau in der Google-Buchsuche).
Roland Winter, Frank Noll: Methoden der Biophysikalischen Chemie. Springer-Verlag, 2013, ISBN 978-3-663-05794-9, S. 437 (eingeschränkte Vorschau in der Google-Buchsuche).
Eva-Maria Neher: Aus den Elfenbeintürmen der Wissenschaft. Wallstein Verlag, 2005, ISBN 978-3-89244-989-8, S. 63 (eingeschränkte Vorschau in der Google-Buchsuche).
Aue, W. P., Bartholdi, E., Ernst, R. R. (1976): Two-dimensional spectroscopy. Application to nuclear magnetic resonance. In: Journal of Chemical Physics, 64: 2229–2246.
Nobelpreisvortrag von Wüthrich (PDF; 399 kB).
Douglas A. Skoog, James J. Leary: Instrumentelle Analytik Grundlagen – Geräte – Anwendungen. Springer-Verlag, 2013, ISBN 978-3-662-07916-4, S. 378 (eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Matthias_Otto-1] Matthias Otto: Analytische Chemie. John Wiley & Sons, 2011, ISBN 3-527-32881-5, S. 270 (eingeschränkte Vorschau in der Google-Buchsuche).

[Horst_Friebolin-2] Horst Friebolin: Ein- und zweidimensionale NMR-Spektroskopie Eine Einführung. John Wiley & Sons, 2013, ISBN 978-3-527-33492-6, S. 423 (eingeschränkte Vorschau in der Google-Buchsuche).

[Roland_Winter,_Frank_Noll-3] Roland Winter, Frank Noll: Methoden der Biophysikalischen Chemie. Springer-Verlag, 2013, ISBN 978-3-663-05794-9, S. 437 (eingeschränkte Vorschau in der Google-Buchsuche).

[Eva-Maria_Neher-4] Eva-Maria Neher: Aus den Elfenbeintürmen der Wissenschaft. Wallstein Verlag, 2005, ISBN 978-3-89244-989-8, S. 63 (eingeschränkte Vorschau in der Google-Buchsuche).

[5] Aue, W. P., Bartholdi, E., Ernst, R. R. (1976): Two-dimensional spectroscopy. Application to nuclear magnetic resonance. In: Journal of Chemical Physics, 64: 2229–2246.

[6] Nobelpreisvortrag von Wüthrich (PDF; 399 kB).

[Douglas_A._Skoog,_James_J._Leary-7] Douglas A. Skoog, James J. Leary: Instrumentelle Analytik Grundlagen – Geräte – Anwendungen. Springer-Verlag, 2013, ISBN 978-3-662-07916-4, S. 378 (eingeschränkte Vorschau in der Google-Buchsuche).