Zwängung
Zwängung oder Zwängsspannung ist die Verspannung von Bauteilen eines Bauwerks. Der Begriff wird verwendet, um Kräfte zu bezeichnen, die von außen auf ein Bauteil einwirken. Sie schränken dessen freie Beweglichkeit (etwa gegenüber Spreiz- und Dehnungsbewegungen oder Senkungen der Gründung) ein und bewirken Eigenspannungen (Druck-, Zug- oder Schubspannungen) im Bauteil. Es kann sich sowohl um externe Zwängungen (siehe auch: Schnittreaktion) als auch um interne Zwängungen (z. B. an den Oberflächen Zug- und im Kern Druckspannungen) handeln. Wenn sie bewusst eingesetzt werden, werden Zwängungen oft als Einspannung bezeichnet.

Im weiteren Sinne können als Zwängung auch die Spannungen bezeichnet werden, die ohne Einwirkung äußerer Kräfte (durch Einspannung), sondern durch Verformungen und Dehnungen innerhalb eines Bauteils zustande kommen. Zwängungen in diesem Sinne können im nanoskopisch über mikroskopischen bis makroskopischen Maßstab auftreten.
Kritisch sind Zwängungen, wenn sie eine Größenordnung annehmen, die zur unerwünschten Verformung von Bauteilen oder bei spröden Baustoffen zur Rissbildung und zum Bruch führt. Zur Vermeidung von Schäden durch Zwängung werden im Bauwesen regelmäßig Bewegungs- und Dehnfugen sowie Bewegungsmöglichkeiten für Tragwerke vorgesehen. Das richtige Maß an Bewegungsfreiheit ist dann gegeben, wenn ein System statisch bestimmt ist.
Beispiele
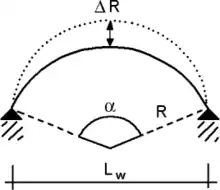
Zwängung tritt häufig auf, wenn Temperaturänderungen zu Spannungen aus Behinderung von thermischer Dehnung führen[2][3]. Berücksichtigt wird dies u. a. durch
- Rohrbögen und andere Dehnungskompensatoren in Heizkreisläufen und Fernwärmeverteilsystemen
- Dehnungsfugen in Estrich und Betonbauteilen wie Fassadentafeln, Fußweg- und Fahrbahnplatten, aber auch in steifem Mauerwerk wie Klinkerschalen
- durch Fest- und Loslagerung von Achsen und Wellen im Maschinenbau.
Feuchtigkeitsaufnahme und -abgabe bewirkt bei bestimmten Baustoffen eine Quellung und Schrumpfung, die zu Verformungen der daraus hergestellten Bauteile führen. Insbesondere bei hölzernen Bauelementen wie Fenstern und Türen wird dies berücksichtigt, indem ausreichend breite Fugen im Falz zwischen Flügel und Zarge vorgesehen werden.
Bei statisch unbestimmten Systemen führt das Nachgeben eines Lagers ebenso wie thermische Dehnung im Allgemeinen zu Zwangsspannungen. Bei problematischen Untergründen oder großen Temperaturschwankungen werden daher oft statisch bestimmte Systeme bevorzugt. (Der Vorteil von statisch unbestimmten Systemen ist, dass beim Versage einzelner Bauteile in manchen Fällen eine Umlagerung der Last auf benachbarte Bauteile ein Versagen der Gesamtkonstruktion verhindern kann.)
Bei der Kombination verschiedener Materialien mit unterschiedlicher Wärmeausdehnung (Sandwichkonstruktion) kommt es bei Temperaturänderungen zu Zwängseigenspannungen (thermischen Spannungen). Beim Stahlbeton treten wenige Zwängsspannungen auf, da sich die Wärmeausdehnung von Beton und Stahl nicht allzu sehr unterscheidet.
Beton schrumpft beim Abbinden, dies kann zu Zwängungen führen[3]. Die resultierenden Zwängsspannungen sind insbesondere beim wasserdichten Beton von weißen Wannen und Talsperren zu berücksichtigen, um die Rissbreite abzuschätzen und Wasserundurchlässigkeit zu garantieren.
Im Maschinenbau macht man sich Zwängung zu nutzen, indem zwei Teile mit einer Presspassung zusammengefügt werden. Im Holz- und Schalungsbau werden Bauteile oft fixiert, indem sie verkeilt werden.
Bei der Rissbreitenbeschränkung im Betonbau (Gebrauchstauglichkeitsnachweis gem. Eurocode) ist im Brückenbau die Zwängung oft das maßgebende Bemessungskriterium.[4]
Einzelnachweise
- Michael Pötzl, Jürgen Maisel: Entwurfsparameter für fugenlose Betonbrücken mit gekrümmtem Grundriß. In: Beton‐ und Stahlbetonbau. Band 100, Nr. 12, 1. Dezember 2005, ISSN 1437-1006, S. 985–990, doi:10.1002/best.200590343 (wiley.com [abgerufen am 5. Dezember 2019]).
- A. Klinkenberg, B. Jäger, H. Saal: Untersuchungen zur statisch optimalen Halterposition bei punktgestützten Glastafeln. In: Stahlbau. Band 67, Nr. 4, 1. April 1998, ISSN 1437-1049, S. 275–280, doi:10.1002/stab.199800940 (wiley.com [abgerufen am 5. Dezember 2019]).
- A. Klinkenberg, B. Jäger, H. Saal: Untersuchungen zur statisch optimalen Halterposition bei punktgestützten Glastafeln. In: Stahlbau. Band 67, Nr. 4, 1. April 1998, ISSN 1437-1049, S. 275–280, doi:10.1002/stab.199800940 (wiley.com [abgerufen am 5. Dezember 2019]).
- Institut für Baustatik und Konstruktion ETH Zürich: 9. Forschungskolloquiums des Deutschen Ausschusses für Stahlbeton (DAfSt): Zusammenfassung der Forschungsberichte. Springer-Verlag, 2013, ISBN 978-3-0348-5291-3, S. 26 (google.at [abgerufen am 5. Dezember 2019]).