Verteilungsgerechtigkeit
Verteilungsgerechtigkeit (lateinisch iustitia distributiva) bezeichnet die Gerechtigkeit von Verteilungsregeln und ihren Ergebnissen. Entsprechend gibt es eine Regelgerechtigkeit und eine Ergebnisgerechtigkeit.
.png.webp)
Die Ergebnisgerechtigkeit ist ein Gerechtigkeitskonzept, das solche Zustände einer Gesellschaft als gerecht definiert, in denen allen Mitgliedern der Gesellschaft der Nutzen aus der Gesellschaft („Ergebnis“) in grundsätzlich gleichem Maße zukommt, jedoch bei einem Verschulden des Mitglieds sein Nutzen aus der Gesellschaft entsprechend gekürzt wird. Als Gegensatz zur Ergebnisgerechtigkeit wird die Regelgerechtigkeit angesehen.
Die aktuelle Ergebnisgerechtigkeit in Bezug auf die Vermögensverteilung ergibt nach den Werten der abgebildeten Weltkarte und der Liste der Länder nach Vermögen pro Kopf eine Spanne von Staatsangehörigen, die 2019 rechnerisch auf unter 1000 USD Vermögensanteil kommen (u. a. Haiti, Sudan, Zentralafrikanische Republik, Burundi, Sierra Leone), bis hin zu Werten über 250.000 USD (u. a. Schweiz, Hongkong, Vereinigte Staaten, Australien, Island). Betrachtet man dabei noch den Unterschied zwischen durchschnittlichem und mittlerem Vermögen, wird erkennbar, dass es auch innerhalb der Staaten erhebliche Ungleichheiten gibt, die vom ca. Doppelten (u. a. Osttimor, Belgien, Rumänien) bis zum über siebenfachen (u. a. Weißrussland, Niederlande, Russland) reichen. Dieser Vergleich weist darauf hin, dass ein Land besonders reiche Bürger hat, deren Vermögen entsprechend weit über dem Durchschnitt liegt.
Antike und Mittelalter
In seinem rechtsphilosophischen Standardwerk, die Nikomachische Ethik, betrachtet Aristoteles die staatlichen Gesetze[1] als Formalobjekt der Regelgerechtigkeit. Er trennt auf zwischen austeilender und ausgleichender Gerechtigkeit.[2] Thomas von Aquin folgt in teilweisem Anschluss daran und nennt das Gemeinwohl.[3] Die Gesetzesgerechtigkeit ist für Thomas die allgemeine Gerechtigkeit, die er der Verteilungsgerechtigkeit (iustitia distributiva) und der Tauschgerechtigkeit (iustitia communtativa) als aus seiner Sicht gesonderte Gerechtigkeitstypen gegenüberstellt.
Experimentelle Spieltheorie
Spiele im Bereich der Verteilungsgerechtigkeit erweisen sich häufig als eine Kombination von Spielen direkt um ein offen benanntes Ergebnis (z. B. Mehrung von Geld) mit Spielen um die Spielregeln selbst. Letztere Spiele werden auch als „Metaspiele“ bezeichnet und sind unter anderem wegen ihrer internen Rückkopplung komplexer als die Spiele um eine einfache Nutzfunktion mit festen Regeln: Regelgerechtigkeit ist Rahmenbedingung und Spielgegenstand zugleich. Scheinbare Paradoxien und Unvernünftigkeiten ergeben sich bei solchen kombinierten Spielen für den Beobachter, der nur Teilaspekte von Verteilungsspielen betrachtet. Im Fall wiederholter Spiele zwischen Gesellschaften werden sogar völlige Selbstaufopferungen einzelner Spieler durch Metaspiele erklärbar.
Zur Untersuchung der Bewertung von „Gerechtigkeit“ bei der Verteilung von Gütern können Variationen des Ultimatum-Spiels verwendet werden. In den folgenden Beispielen wurde die Sanktionierung von Verteilung in einem weltweiten Forschungsprojekt von 12 US-amerikanischen und einer kolumbianischen Universität untersucht.[4] Dabei können diese Sanktionierungen auch Nachteile für den Sanktionierenden haben, die dieser jedoch hinnimmt:
- „Ultimatum“ für zwei Spieler: Spieler A wird ein Geldbetrag angeboten, den er mit Spieler B teilen muss. Spieler A bietet Spieler B einen Anteil an (zwischen mehr als 0 % und maximal 100 %). Erst wenn Spieler B das Angebot annimmt, werden A und B ihre von A entschiedenen Anteile am Geldbetrag ausgezahlt. Wenn Spieler B das Angebot nicht annimmt, dann erhält keiner etwas. Beide Spieler verlieren.
- „Ultimatum“ für drei Spieler: Wie „Ultimatum“ für zwei Spieler, aber ein dritter Spieler C kann Spieler A zusätzlich „bestrafen“, sollte er A für zu „egoistisch“ halten. Spieler C erhält dazu ohne jede Bedingung einen Geldbetrag und das Recht, Spieler A für ein unangemessenes Angebot an Spieler B zu bestrafen. Dabei bleibt es Spieler C überlassen, zu beurteilen, was ein unangemessenes Angebot sei. Wenn sich Spieler C für eine Bestrafung von A entscheidet, bestimmt er, wie viel Strafe A zahlen muss. Die Kosten der Bestrafung für Spieler C: Ein Drittel des Betrages, den er als Strafe für den Spieler A bestimmt hat.
- „Diktator“ für zwei Spieler: Wie „Ultimatum“ für zwei Spieler, aber B muss das Angebot annehmen. B kann also nicht A durch Verzicht bestrafen.
Bei zwei von den beschriebenen drei „Spielen“ ist die Bestrafung mit Kosten verbunden. Damit kann der Bestrafung ein Wert zugewiesen werden. Man nimmt an, dass Menschen nur dann selbstlos handeln, wenn Egoismus sanktioniert wird. Allerdings gab es Unterschiede in der Bewertung der Angemessenheit des Anteils, den B von A erhält. In zwei Fällen in Accra (Ghana) und bei den Sanquinaga (Kolumbien) nahmen B-Spieler Anteile auch dann nicht an, wenn sie zu hoch waren. Die B-Spieler lehnten hier nicht nur unangemessenen Egoismus ab, sondern auch eine aus ihrer Sicht unangemessene Begünstigung ihrer selbst.[5]
Systemtheorie und Ökonometrie
In abgeschlossenen Systemen ist Gleichverteilung in allen Kategorien das wahrscheinlichste Ergebnis der in solchen Systemen stattfindenden Prozesse. Die Entropie des Systems hat dann ihr Maximum erreicht. Menschliche Gesellschaften sind beschränkt offene Systeme, denn sie können Entropie exportieren, wenn auch nur in einem begrenzten Maß. Eine Möglichkeit, die Entropie in der Gesellschaft zu senken, ist die Steigerung der Ungleichverteilung in irgendeiner von der Gesellschaft beeinflussbaren Kategorie. Ressourcen wie Einkommen und Vermögen stellen hier eine der wichtigsten Kategorien dar. Was ist hier im Ergebnis eine „gerechte“ Einkommens- oder Vermögensverteilung?
In der Ökonometrie gibt es viele verschiedene Maßzahlen für die ungleiche Verteilung von Vermögen und Einkommen, darunter der Gini-Koeffizient, die Hoover-Ungleichverteilung und der Theil-Index. Die Ökonometrie zeigt, dass der Grad der Verteilungsungleichheit von Ressourcen auf Menschen sehr verschiedene Auswirkungen hat. Es geht nicht um „Gleichheit oder Ungleichheit“, sondern um den Grad von Gleichheit beziehungsweise Ungleichheit. Wenn diese Tatsache nicht berücksichtigt wird, werden Diskussion über ökonomische Gleichheit unnötig kompliziert und normativ. Es gibt keinen „Umverteilungsdruck“, der rein proportional zur Ungleichverteilung wächst, sondern es gibt ein Verhalten, aus dem sich Optimalität ableiten lässt, wie anhand der drei Ungleichverteilungsmaße gezeigt werden kann:
- Der Gini-Koeffizient ist ein ohne Bezug zu realen Ausgleichsprozessen konstruiertes Ungleichheitsmaß. Dank seiner Popularität haben Sozialwissenschaftler jedoch viele Erfahrungen[7] sammeln können, welche Bedeutung unterschiedliche Gini-Koeffizienten haben.
- Die Hoover-Ungleichverteilung ist das Einfachste aller Ungleichheitsmaße. Sie beschreibt den Umverteilungsdruck in einer Gleichheit anstrebenden Gesellschaft, in der ein Ausgleich basierend auf vollständiger Information mit minimalem Aufwand erreicht werden könnte.
- Der symmetrisierte Theil-Index (Mittelwert aus Theil-L und Theil-T-Index) ähnelt der Hoover-Ungleichverteilung. Jedoch werden hier die aggregierten einzelnen Abweichungen von der Parität zusätzlich mit ihrer informationstheoretischen Bedeutung gewichtet. Der symmetrisierte Theil-Index beschreibt den Umverteilungsdruck in einem Gesellschaftssystem, in der ein Ausgleich durch zufällige Bewegungen von Menschen und Ressourcen erfolgen würde. (Jedes abgeschlossene Gesellschaftssystem wäre ein solches System. Um intern Ungleichverteilung anwachsen zu lassen, müssen Systeme ihre Umwelt - also häufig den mit Nachbarsystemen geteilten Raum - mit Entropie belasten können, woraus sich dann wieder entsprechende intersystemische Verteilungskonflikte ergeben.)
Liegt der symmetrisierte Theil-Index über der Hoover-Ungleichverteilung, dann treibt die Ungleichverteilung einen Ausgleich von sich aus an, denn die stochastisch erfolgende Umverteilung ist stärker, als eine intelligent kontrollierte Umverteilung. (Bei hoher Ungleichverteilung - z. B. bei hoher Konzentration von Ressourcen auf wenige Orte im Raum - gibt es naturgemäß viel Spielraum für Umverteilung.)
Liegt der symmetrisierte Theil-Index unter der Hoover-Ungleichverteilung, dann wäre eine kontrollierte Umverteilung wirksamer. Allerdings müsste dann auch bewusst Aufwand zur Steuerung der Umverteilung getrieben werden, wodurch Kosten entstünden, die einen Gewinn an Gerechtigkeit wieder schmälerten. In diesem Bereich hat die Gleichverteilung auch schon einen recht hohen Grad erreicht. Völlige Gleichverteilung wäre dann maximale Entropie. Leben ist jedoch dadurch gekennzeichnet, dass lebende Systeme aktiv einen Mindestabstand[8] ihrer aktuellen Entropie zur maximalen Entropie bewahren. Hieraus ergibt sich die Notwendigkeit eines Mindestmaßes an Ungleichheit. In dessen Nähe finden beispielsweise skandinavische Gesellschaften ihren Arbeitspunkt, insbesondere bei sehr guter Ressourcenversorgung (Norwegen und m. E. auch Island).
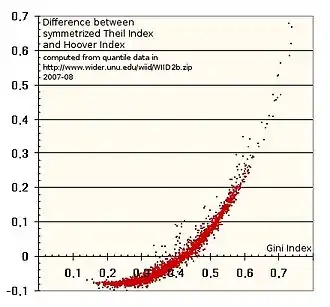
Zieht man nun die Hoover-Ungleichheit von dem symmetrisierten Theil-Index ab und trägt diese Differenz über den zugehörigen Gini-Koeffizienten auf (siehe Grafik), dann ergeben sich zwei Zonen. Unterhalb eines (basierend auf Dezilen errechneten) Gini-Koeffizienten von etwa 40 % sind die sich aus realen Einkommensverteilungen ergebenden Differenzen zwischen Theil-Index und Hoover-Ungleichheit negativ. Darüber sind sie positiv. Beobachtbar ist nun, dass die Wirtschaftsgebiete mit der höchsten Lebensqualität alle in der Nähe dieses Durchgangs bei 40 % durch die Null-Linie angesiedelt sind. In der Ressourcenlage der Gegenwart liegt hier ein optimaler Wert für Ungleichheit, der sich hypothetisch bei einem freien Spiel der Kräfte von selbst einstellt und nach dem Mythos von der unsichtbaren Hand nicht erst durch normative Steuerung angestrebt werden muss. Sehr große Abweichungen von diesem Wert (Gini-Koeffizienten unter etwa 20 % oder über etwa 60 % bei auf gleich große Dezile verteilten Einkommen[9]) sind beobachtbar immer mit der Anwendung starker Gewalt verbunden.
Die hier beschriebenen nicht-normativen Verhältnisse schreiben dem Menschen nicht vor, welche Art von Verteilung gerecht sei, sondern sie beschreiben, in welchem unterschiedlichen Grad sich Ungleichverteilungen den Menschen darstellen und welche informationstheoretische Bedeutung unterschiedliche Ungleichverteilungen haben. Die Entscheidung, welche Verteilung gerecht sei, bleibt normativ und darum umstritten.
Literatur
- Stefan Arnold: Vertrag und Verteilung: die Bedeutung der iustitia distributiva im Vertragsrecht, zugleich Habilitationsschrift an der Universität München 2013. Mohr Siebeck, Tübingen 2014, ISBN 978-3-16-152986-3.
- Stefan D. Josten: Ungleichheit, staatliche Umverteilung und gesamtwirtschaftliches Wachstum. 2008, ISBN 978-3-8305-1377-3.
Weblinks
- Michael Allingham: Distributive Justice. In: J. Fieser, B. Dowden (Hrsg.): Internet Encyclopedia of Philosophy.
- Politikwissenschaftliche Literatur zum Thema Verteilungsgerechtigkeit und Armut in Deutschland und Europa, Auswahlbibliografie der Annotierten Bibliografie der Politikwissenschaft
Anmerkungen
- Nikomachische Ethik, 3,5, 1130b;
- Uwe Wesel: Geschichte des Rechts. Von den Frühformen bis zur Gegenwart. 3. überarbeitete und erweiterte Auflage. Beck, München 2006, ISBN 3-406-47543-4. Rn. 124.
- Vergleiche insgesamt: Summa theologica, II-II, 57-79; Michael Schramm: Gerechtigkeit. In: LThK 3, Band 4, S. 498–500.
- Joseph Henrich u. a.: Costly Punishment Across Human Societies. In: Science. Band 312, 23. Juni 2006, doi:10.1126/science.1127333. Christopher Schrader: Ultimatum auf Fidschi. In: Süddeutsche Zeitung. 23. Juni 2006 (Artikel zu Henrich u. a.).
- Joseph Henrich u. a.: Costly Punishment Across Human Societies. 2006, S. 1767, Abb. 1.
- World Income Inequality Database
- Y.Amiel, F.A.Cowell: Thinking about inequality. 1999, ISBN 0-521-46696-2
- ISO/IEC DIS 2382-16:1996 definiert diesen Abstand in der Informationstheorie als „Redundanz“.
- Bei der Angabe von Ungleichverteilungskoeffizienten sollten immer Angaben über die Art und Weise der Datenaggregation gemacht werden. Eine Möglichkeit ist, die Art der Quantile zu beschreiben, auf deren Daten sich die Berechnung stützt. In diesem Fall sind das gleich große Dezile. In Hauser/Becker: Verteilung der Einkommen, Gutachten für den Zweiten Armuts- und Reichtumsbericht der Bundesregierung, Frankfurt 2004, S. 96; zitiert in DGB-Präsentation Verteilungsgerechtigkeit, S. 34 werden diese Dezile für Deutschland auch angegeben. Auswertung (Jahr und Gini-Koeffizient): 1998: 38.9 % und 2003: 41.7 %