Ungleichverteilungsmaß
Ein Ungleichverteilungsmaß beschreibt den Grad der Ungleichverteilung einer Größe gegenüber einer anderen Größe. In den Sozialwissenschaften sind diese Größen auf der einen Seite häufig Ressourcen wie Einkommen oder Vermögen und auf der anderen Seite die Anzahl derer, die über Einkommens- und Vermögensanteile verfügen. Mit Ungleichverteilungsmaßen wird angegeben, zu welchem Grad die Zuordnung von Ressourcen zu Menschen von einer Gleichverteilung abweicht. Grundlage der Ermittlung ist eine aufsteigend sortierte Liste der zu untersuchenden Verteilungsgröße. Eine sinnlich eindrückliche Darstellung von Ungleichverteilung ist Pen’s Parade. Im Folgenden wird ein kurzer Überblick über die wichtigsten Ungleichverteilungsmaße gegeben.
Überblick
Hoover-Ungleichverteilung
Als einfachstes Ungleichverteilungsmaß basiert die Hoover-Ungleichverteilung auf einer Verteilung, bei der eine Ungleichverteilung in eine Gleichverteilung zu jeder Zeit voll informiert überführt wird. Die Hoover-Ungleichverteilung ist 0 (oder 0 %) bei völliger Gleichverteilung und 1 (oder 100 %) bei maximaler Ungleichverteilung. Sie gibt direkt an, welcher Anteil beispielsweise eines ungleichverteilten Gesamteinkommens bewegt werden müsste, um eine völlige Gleichverteilung zu erzielen.
Theil-Index
Demgegenüber liegt dem Theil-Index das Verteilungsmodell einer völlig ungeregelten Wirtschaft zugrunde, in dem die Umverteilung in einem rein stochastischen Prozess erfolgt. Zu keiner Zeit werden bei diesem Modell von den darin wirkenden Akteuren und Prozessen irgendwelche Informationen über die aktuelle Ressourcenverteilung ausgewertet. Der Theil-Index ist ein aus der Informationstheorie abgeleitetes Ungleichverteilungsmaß. Er gehört zur Familie der Entropiemaße.[1]
Gini-Koeffizient
Zwar kommt der Theil-Index zunehmend häufiger zum Einsatz, jedoch wird der Gini-Koeffizient immer noch am häufigsten verwendet. Er ist eine Auswertung der Lorenzkurve und wirkt damit zwar anschaulicher als andere Ungleichverteilungsmaße, aber ihm lag bei seiner Entwicklung kein Verteilungsmodell zugrunde. Der Gini-Koeffizient ist 0 (oder 0 %) bei völliger Gleichverteilung und 1 (oder 100 %) bei maximaler Ungleichverteilung. Seine Berechnung lässt sich sehr anschaulich mit den Mitteln der Geometrie darstellen; was ein gemessener Gini-Koeffizient jedoch sozialwissenschaftlich bedeutet, lässt sich nicht geometrisch vermitteln.[2] Die langjährige und häufige Verwendung des Gini-Koeffizienten führte jedoch zu einem empirischen Verständnis für die Bedeutung der Gini-Koeffizienten. Auch gibt es empirische Untersuchungen, die den Zusammenhang zwischen subjektiven Wertungen von Ungleichverteilungen und den dazugehörigen Ungleichheitsmaßen erforschen.[3]
Hoover-Ungleichverteilung
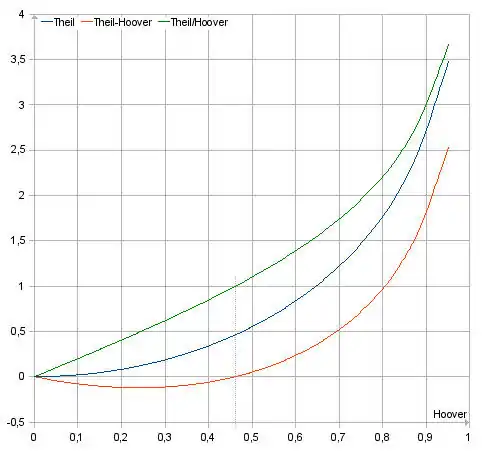
Die Grafik illustriert den Verlauf von T, T-H und T/H als Funktion von für Gesellschaften, die in zwei Quantile aufgeteilt sind, in denen ein Anteil von Euro einem Anteil von Menschen zugeordnet ist und ein Anteil von Euro einem Anteil von Menschen zugeordnet ist, wobei gilt (z. B. das „80:20-Pareto-Prinzip“ mit und , woraus und resultiert). Für derart partitionierte Gesellschaften, sind der Theil-Index und der symmetrierte Theil-Index gleich. Einen gleichen Verlauf nehmen auch der Gini-Koeffizient und die Hoover-Ungleichverteilung . Unter diesen Voraussetzungen gilt .
Die Hoover-Ungleichverteilung ist das einfachste aller Ungleichverteilungsmaße. Im Englischen ist dieses Ungleichverteilungsmaß unter anderem auch als „Robin-Hood-Index“ bekannt. Die Hoover-Ungleichverteilung ist 0 (oder 0 %) bei völliger Gleichverteilung und 1 (oder 100 %) bei maximaler Ungleichverteilung. Sie gibt direkt an, welcher Anteil beispielsweise eines ungleichverteilten Gesamteinkommens bewegt werden müsste, um eine völlige Gleichverteilung zu erzielen.
Man kann mit dem Hoover-Index die Wirkung einer Steuerprogression direkt messen: Im Jahr 2001 ergab sich eine Hoover-Ungleichverteilung[4] der Brutto-Einkommen gegenüber den Steuerzahlern von 0,332. Bei einer Einheitssteuer ohne Freibetrag läge auch die Ungleichverteilung der Netto-Einkommen bei 0,332. Tatsächlich ergab sich aber eine Hoover-Ungleichverteilung von 0,300. Es wurden also durch die Steuerprogression 3,2 % des Netto-Einkommens „von oben nach unten“ umverteilt.
Die Hoover-Gleichverteilung ist 1 (oder 100 %) abzüglich der Hoover-Ungleichverteilung. Eine für ein Volkseinkommen mit der Hoover-Gleichverteilung berechnete Wohlfahrtsfunktion ergibt sich, wenn das Volkseinkommen mit der Hoover-Gleichverteilung multipliziert wird. Diese Wohlfahrtsfunktion hat eine konkrete Bedeutung: Sie ist der Anteil des Volkseinkommens, der unangetastet bliebe, wenn man das Volkseinkommen so umverteilen würde, dass sich eine völlige Gleichverteilung ergäbe.
Wird das Volkseinkommen mit der Hoover-Ungleichverteilung multipliziert oder wird von dem Volkseinkommen die Wohlfahrtsfunktion abgezogen, dann ergibt sich der Anteil des Volkseinkommens, der insgesamt bewegt werden müsste, wenn eine völlige Gleichverteilung mit minimalem Aufwand durchgeführt werden sollte. Dazu wäre eine perfekte Planung unter der Voraussetzung vollständiger Informiertheit erforderlich.
Theil-Index
Der Theil-Index ist ein aus der Informationstheorie abgeleitetes Ungleichverteilungsmaß. Er gehört zur Familie der Entropiemaße.[1][5] Der Theil-Index wird gelegentlich fälschlicherweise auch als Theil-Entropie bezeichnet. Tatsächlich handelt es sich dabei aber um eine Redundanz, denn er ist die Differenz zwischen einer sich bei Gleichverteilung einstellenden maximalen Entropie und einer sich aus einer Ungleichverteilung ergebenden aktuellen Entropie.
Der Theil-Index ist 0 bei völliger Gleichverteilung und 1 bei einer Ungleichverteilung, bei der 17,6 % der Ressourcenbesitzer über 82,4 % der Gesamtressourcen und umgekehrt 82,4 % der Ressourcenbesitzer über 17,6 % der Ressourcen verfügen. Als Merkhilfe kann hierbei dienen, dass diese Ungleichverteilung für einen Theil-Index von 1 ziemlich nahe an der 80:20-Verteilung liegt, die als „Pareto-Prinzip“ bekannt ist. Bei einer höheren Ungleichverteilung ist der Theil-Index größer als 1.
Im Unterschied zur Hoover-Ungleichverteilung werden bei der Berechnung des Theil-Index nicht nur Disparitäten aggregiert, sondern diese Disparitäten werden mit ihrem Informationsgehalt gewichtet. Daraus ergibt sich dann eine Kennzahl, die nicht nur den Anteil der für einen Ausgleich umzuverteilenden Ressourcen beschreibt, sondern auch die Aufmerksamkeit, die die Ungleichverteilung hervorruft.
Den Theil-Index gibt es in zwei Ausführungen. Der Theil-L-Index beschreibt die Verteilung von Ressourcen zu Menschen, der Theil-T-Index beschreibt die Verteilung von Menschen zu Ressourcen. Der Mittelwert beider Indizes ist ein symmetrierter Theil-Index, der strukturell der einfachen Hoover-Ungleichverteilung sehr ähnlich ist (siehe Hauptartikel).
Bei der Berechnung von Ungleichverteilungsmaßen werden heute oft beide Theil-Indizes angegeben, manchmal auch zusätzlich zum Gini-Koeffizient.
Die Normierung der Theil-Indizes in den Bereich zwischen 0 und 1 (beziehungsweise zwischen 0 % und 100 %) erfolgt mit der Operation .
ist die Theil-L-Gleichverteilung. Eine für ein Volkseinkommen mit der Theil-L-Gleichverteilung berechnete Wohlfahrtsfunktion ergibt sich, wenn das Volkseinkommen mit der Theil-L-Gleichverteilung multipliziert wird. Im Artikel zum Theil-Index wird die Anwendung des Theil-L-Indexes auf die Berechnung der Wohlfahrtsfunktion eingehender erläutert. Eine Pro-Kopf-Wohlfahrtsfunktion kann man als ein „empfundenes Durchschnittseinkommen“ interpretieren und als Alternative zum Median verwenden.
Wird das Volkseinkommen mit dem Theil-L-Index multipliziert oder wird von dem Volkseinkommen die mit dem Theil-L-Index berechnete Wohlfahrtsfunktion abgezogen, dann ergibt sich der Anteil des Volkseinkommens, der insgesamt bewegt werden würde, wenn eine völlige Gleichverteilung unter der Bedingung einer aus planerischer Sicht ausschließlich den Gesetzen des Zufalls unterworfenen Verteilung erreicht werden sollte. Das Verteilungsmodell entspräche dem Modell des freien Marktes. Dazu müsste das System, in dem die Verteilung stattfindet, vollständig von seiner Umwelt abgeschlossen und sich selbst überlassen werden. (Wird kein Einkommen bewegt, dann wäre eine Gleichverteilung auch durch Bewegung der Einkommensbezieher in einem dem Zufall unterworfenen Verteilungsprozess denkbar. Die Zahl der insgesamt bewegten Bezieher wäre in diesem Fall das Produkt aus dem Theil-T-Index und der Anzahl der Einkommensbezieher.) Bei hohen Ungleichheiten ergibt sich mit dem Theil-Index ein Umverteilungsvolumen, dass das mit dem Hoover-Ungleichverteilung berechnete Volumen übersteigt. Bei kleinen Ungleichheiten liegt das errechnete Umverteilungsvolumen zunächst unterhalb des mit der Hoover-Ungleichverteilung berechneten Volumens, ein Ausgleich scheint also nicht stattfinden zu können. Jedoch ergeben sich im Verlauf des theoretisch angenommenen Ausgleichsprozesses neue Werte für den Theil-Index, die sich in der Nähe von Null den Werten der Hoover-Ungleichverteilung wieder annähern.
In realen Volkswirtschaften liegt immer eine Mischung aus einer dem Zufall überlassenen und einer der Planung unterworfener Verteilung vor. Im (nur theoretisch vorstellbaren) geschlossenen Wirtschaftssystem führt diese Verteilung zum Ausgleich, im offenen System dagegen kann die Ungleichverteilung auch ansteigen, zum Beispiel durch zeitlich und örtlich ungleichverteilten Zugriff zu Ressourcen in der Umwelt des Systems. Aus diesem Grund sind sowohl die Hoover-Ungleichverteilung wie auch der Theil-Index relevante Maße. Die Differenz zwischen beiden Ungleichverteilungsmaßen ist für den Großteil der Volkswirtschaften kleiner als 0,1 (siehe „Vergleich des Theil-Index mit der Hoover-Ungleichverteilung“ im Hauptartikel Theil-Index).
Gini-Koeffizient
Der Gini-Koeffizient ist das in den Sozialwissenschaften am häufigsten verwendete Ungleichverteilungsmaß. Er ist 0 (oder 0 %) bei völliger Gleichverteilung und 1 (oder 100 %) bei maximaler Ungleichverteilung. Seine Berechnung lässt sich sehr anschaulich mit den Mitteln der Geometrie darstellen; was ein gemessener Gini-Koeffizient jedoch sozialwissenschaftlich bedeutet, lässt sich nicht geometrisch vermitteln.[2]
Die langjährige und häufige Verwendung des Gini-Koeffizienten führte jedoch zu einem empirischen Verständnis für die Bedeutung der Gini-Koeffizienten. Auch gibt es empirische Untersuchungen, die den Zusammenhang zwischen subjektiven Wertungen von Ungleichverteilungen und den dazugehörigen Ungleichheitsmaßen erforschen.[6] Den Gini-Koeffizienten verwendet man zumindest dann, wenn Forschungen fortgesetzt werden sollen, in denen bereits mit diesem Ungleichverteilungsmaß gearbeitet wurde.
Die Sozialstatistik der EU arbeitet mit dem S80/S20-Einkommensquintilverhältnis.
Andere Ungleichverteilungsmaße
In den Sozialwissenschaften gibt es etwa 50 Ungleichverteilungsmaße.[7] Viele sind miteinander verwandt oder parallel entwickelt worden. In der gegenwärtigen Forschung werden zunehmend Entropiemaße wie der Theil-Index verwendet. In der Wikipedia existieren Hauptartikel zu diesen weiteren Ungleichverteilungs- und Konzentrationsmaßen:
Siehe auch
Einzelnachweise
- Frank A. Cowell: Theil, Inequality and the Structure of Income Distribution. (PDF; 312 kB) London School of Economics and Political Sciences, 2002, 2003 (mit Bezugnahmen zu der „Klasse der Kolm-Indizes“, das sind Maßzahlen für Ungleichverteilungen wie z. B. der Theil-Index)
- Eberhard Schaich: Lorenzkurve und Gini-Koeffizient in kritischer Betrachtung. In: Jahrbücher für Nationalökonomie und Statistik, 185, 1971, S. 193–208.
- Y. Amiel, F. A. Cowell: Thinking about inequality. 1999, ISBN 0-521-46696-2
- Berechnet basierend auf der Steuerstatistik (nicht Einkommensstatistik) in den Grunddaten des Bundesamtes für Statistik, November 2005.
- siehe auch Entropie (Sozialwissenschaften)
- Y. Amiel, F.A. Cowell: Thinking about inequality. 1999, ISBN 0-521-46696-2
- Philip B. Coulter: Measuring Inequality. 1989.