Vektorregelung
Die Vektorregelung ist ein Regelungskonzept, bei dem sinusförmige – oder als weitgehend sinusförmig angenommene – Wechselgrößen (beispielsweise Wechselspannungen und Wechselströme) nicht direkt in ihrem zeitlichen Momentanwert, sondern in einem um den Phasenwinkel innerhalb der Periode bereinigten Momentanwert geregelt werden. Zu diesem Zweck werden die erfassten Wechselgrößen jeweils in ein mit der Frequenz der Wechselgrößen rotierendes Koordinatensystem übertragen. Innerhalb des rotierenden Koordinatensystems ergeben sich dann aus den Wechselgrößen Gleichgrößen, auf die alle üblichen Verfahren der Regelungstechnik angewandt werden können.
Allgemeines
Aus praktischen Gründen wird bei der Regelung von elektrischen Größen für das rotierende Koordinatensystem praktisch immer eines mit zwei senkrecht aufeinander stehenden Achsen d und q gewählt. Dies hat den Vorteil, dass es mit der Raumzeigerdarstellung (englisch space vector) von Wechselspannungen und -strömen und ihrem Bezug zueinander identisch ist, wodurch sich die entsprechenden Modelle der elektrischen Maschinen direkt einsetzen lassen.
Durch diese Vektorregelung, die mit Bezug auf das Drehfeld einer elektrischen Maschine auch feldorientierte Regelung genannt wird, erreicht ein Frequenzumrichter für Elektromotoren eine erweiterte Drehzahl- und Positioniergenauigkeit gegenüber einer Regelung, die lediglich durch einen Tiefpass gefilterte Effektivwerte von Strömen und Spannungen einer oder gar mehrerer Periode(n) verwendet.
Die Anwendung der Vektorregelung ist aber nicht auf Antriebe beschränkt, auch für Stromrichter zur Einspeisung in Netze ist das Prinzip einsetzbar. Dabei können Frequenz und Phase entweder vom Netz vorgegeben werden, sie werden dann, wie bei der Antriebsregelung auch, gemessen, oder aber der Stromrichter gibt, z. B. in einem Inselnetz, diese Größen selbst vor.
Die Vektorregelung findet die Grenze ihrer Anwendbarkeit, wenn die zu steuernden und zu messenden Größen nicht mehr hinreichend sinusförmig sind. In diesem Fall kann das Übertragen in das rotierende Koordinatensystem nur den Einfluss der Grundschwingung eliminieren, die Oberschwingungen bleiben zurück und können vom Regler nicht von einer Beaufschlagung mit Störgrößen unterschieden werden. Für praktische Anwendungen in der Antriebstechnik ist ein Filtern der Oberschwingungen jedoch meistens ausreichend. Bei Anwendungen für Stromrichter, die nicht auf mechanische Antriebe wirken oder nicht durch diese gestützt werden, sondern z. B. ihrerseits direkt auf andere Stromrichter arbeiten (z. B. Batteriestromrichter im Inselbetrieb versorgt 230-V~-Kompaktleuchtstofflampen), muss dies jedoch beachtet werden.
Vektorregelung bei Synchronmaschinen
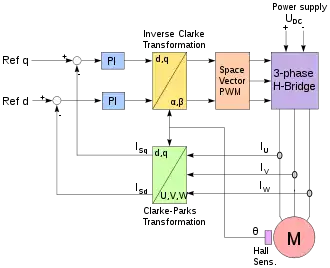
Sind Statorfluss und Statorstrom im rotierenden D-Q-Feld beim Synchronmotor parallel, so ist das Drehmoment gleich Null. Das rotorbezogene d/q-System wird mithilfe der Clarke-Transformation und anschließender d/q-Transformation (Park-Transformation) aus dem statorbezogenen dreiphasigen System berechnet. Die d- und q-Vektoren stehen aufeinander senkrecht, der q-Wert bildet das Drehmoment und der d-Wert die magnetische Flussdichte ab und können ähnlich wie bei einer Gleichstrommaschine mit PI-Regler modelliert werden. Durch von außen vorgegebenen q-Referenzwert kann das Drehmoment der Maschine beeinflusst werden. Bei im Rotor permanent erregten Synchronmotoren, typisch ist dies bei den sogenannten bürstenlosen Gleichstrommotoren (BLDC), ist der d-Referenzwert im Grunddrehzahlbereich Null, sofern die d- und q-Induktivitäten gleich groß sind, es also keinen Reluktanzbeitrag zum Drehmoment gibt. Im Feldschwächbereich wird ein negativer d-Referenzwert verwendet, um die induzierte Spannung zu limitieren. Mit einer inversen Transformation und anschließender Raumzeigermodulation (englisch Space Vector PWM) werden die Ansteuersignale für den dreiphasig ausgeführten Vierquadrantensteller gebildet.
Zur Ausregelung des Raumvektors im rechten Winkel ist ein Regelkreis mit Rückkopplung zur Maschine erforderlich, welcher die Lage des Polrades angibt. Diese Rückkopplung wurde bei Synchronmaschinen meist mit drei Hallsensoren realisiert. Da diese jedoch fehleranfällig sind und nur eine geringe Winkelauflösung bieten, werden in Servoantrieben meist Encoder (Resolver, optische Inkremental- und Absolutwertgeber oder induktive Geber) eingesetzt. Sensorlose Regelungen können bei Blockkommutierung durch das Zurückmessen der im Motor induzierten Gegenspannung realisiert werden. Diese Rückkopplung hat jedoch insbesondere bei kleinen Geschwindigkeiten zunehmende Nachteile. Eine weitere, sensorlose Methode für das erfassen der Rotorposition bei niedrigen Drehzahlen ist das Messen der Wicklungsinduktivitäten. Diese ändern sich, je nachdem, ob sich ein Permanentmagnet über der gemessenen Spule befindet, oder nicht.
Eine weitere Möglichkeit, eine Synchronmaschine sensorlos mittels Vektorregelung zu betreiben, basiert auf mathematischer Berechnung der benötigten Regelparameter. Ausschlaggebend hierfür ist ein realistisches und möglichst genaues Softwaremodell der Maschine. Ein digitaler Signalprozessor schätzt mithilfe dieses Maschinenmodells die zur Vektorregelung benötigten Parameter wie beispielsweise den Rotorwinkel und die Drehzahl. Die einzigen bei dieser Methode benötigten Messgrößen sind die drei Statorströme der Maschine. Da der Sternpunkt der Maschine (sofern vorhanden) für gewöhnlich nicht angeschlossen wird, genügt das Messen von zwei Statorströmen, womit zwangsläufig auf den dritten Statorstrom geschlossen werden kann.
Vektorregelung bei Asynchronmaschinen
Die Vektorregelung von Drehfeldmaschinen wurde 1968 von K. Hasse an der TH Darmstadt erfunden und unabhängig davon auch in der Doktorarbeit von Felix Blaschke 1973 an der TU Braunschweig mit dem Titel „Das Verfahren der Feldorientierung zur Regelung der Drehfeldmaschine“ beschrieben. Bei der Vektorregelung der Asynchronmaschine ist das magnetische Luftspaltfeld ausschlaggebend für das Betriebsverhalten. Der Magnetisierungsstrom muss hierbei im Falle des Grunddrehzahlbereichs drehzahlunabhängig konstant gehalten werden.
Asynchronmaschinen können zur Leistungssteigerung ebenfalls mit vektormodulierter Frequenz angesteuert werden. Hierbei sind der Wirk- und Blindstrom Iw und Iu interessant. Der Blindstrom sorgt für eine Magnetisierung des Ständers, der Wirkstrom für das Drehmoment. Da sich der Blindwiderstand X vom Ständer mit der Frequenz ändert, der ohmsche Widerstand R jedoch bei Frequenzänderungen konstant bleibt, ist die U/f-Kennlinie bei einem Asynchronmotor nichtlinear. Insbesondere bei niedrigen Frequenzen ist der Spannungsabfall an R so groß, dass kein voller Blindstrom mehr durch X fließen kann und die Maschine dann wegen ungenügender Magnetisierung an Drehmoment verliert. Dies ist auch der Grund, weshalb man sehr kleine Geschwindigkeiten mit Asynchronmaschinen nur noch schlecht ausregeln kann und der Asynchronmotor zum genauen Positionieren ungeeignet ist.
Um diese Nachteile bei kleinen Geschwindigkeiten auszugleichen, bieten viele Frequenzumrichter, welche nach der U/f-Kennlinie arbeiten, für kleine Geschwindigkeiten einen „Boost“-Betrieb an, bei welchem die über dem Ständer R abfallende Spannung zusätzlich eingespeist wird. Allerdings sind derart feste Boost-Faktoren lediglich ein Kompromiss für eine mittlere Drehmomentabgabe, da das Drehmoment ebenfalls einen Wirkstrom verursacht. Dieser Wirkstrom hat einen ebensolchen Spannungsabfall im Ersatzschaltbild des Ständer R zur Folge, weshalb der gewünschte Blindstrom wiederum nicht optimal ist. Bei einem fehlerhaften Blindstrom ist damit entweder das Drehmoment zu gering, oder die Maschine hat bei Übermagnetisierung einen hohen Eisenverlust in Wärme umzusetzen. Außerdem verändert sich der Wirkwiderstand R der Maschine bei Erwärmung auf einen besonders bei niedrigen Drehzahlen durchaus nicht mehr zu vernachlässigenden Wert.
An dieser Stelle greift nun die Vektormodulation ein und führt den Drehfeldvektor in einer geschlossenen Regelschleife nach, welche idealerweise sämtliche Störeinflüsse des Systems berücksichtigt. In der Praxis können damit auch bei Asynchronmaschinen zum Positionieren bis zur Geschwindigkeit Null nahezu ideale Servoeigenschaften erreicht werden. Bei verschiedenen Frequenzumrichtern ist es heute Stand der Technik, dass die Regelung der Vektormodulation adaptiv arbeitet. Unbekannte Maschinenmodelle werden selbst erlernt und applikationsspezifische Lastsprünge automatisch nachgeregelt.
Siehe auch
Literatur
- Nguyen Phung Quang, Jörg-Andreas Dittrich: Vector control of three-phase AC machines. 2. Aufl. Springer, Berlin 2015, ISBN 978-3-662-46914-9.
Weblinks
- In das Thema Raumzeiger einführende Studienarbeit, Präsentation und Animationen
- Anwendungsbeispiel und Theorie der Feldorientierten Regelung mit Sensor von Atmel (PDF; 467 kB)
- Anwendungsbeispiel und Theorie der Feldorientierten Regelung ohne Sensor von Microchip (PDF; 486 kB)
- Position detection and start-up algorithm of a rotor in a sensorless BLDC motor utilising induction variation PREM (PDF; 1256 kB)
- Dissertation (PDF; 2,0 MB) zur Feldorientierten Regelung der permanenterregten Synchronmaschine