Raumzeigerdarstellung

Unter dem Begriff Raumzeigerdarstellung versteht man in der Elektrotechnik die Darstellung von physikalischen Größen im Dreiphasensystem als Zeiger in einer komplexen Ebene. Das Hauptanwendungsgebiet der Raumzeigerdarstellung ist die Beschreibung von Magnetfeldern, Spannungen und Strömen in Drehfeldmaschinen.

In der Wechselstromtechnik wird statt der Raumzeigerdarstellung die einfache Zeigerdarstellung verwendet.

Raumzeiger

Statorspulen im statorfesten αβ-Koordinatensystem. Jede Spule erzeugt ein Magnetfeld mit vorgegebener Richtung. Durch Überlagerung dieser ergibt sich der resultierender Raumzeiger B_g

Die Grundidee der Raumzeigerdarstellung beruht darauf, dass die Nullbedingung erfüllt ist: Der Sternpunkt (sofern vorhanden) der Last ist nicht mit dem Neutralleiter des Dreiphasensystems verbunden. Dadurch ist die Summe der Phasenströme immer null. Dann kann man durch Kenntnis zweier Größen auf die Dritte schließen. Also wird ein solches Dreiphasensystem durch zwei Größen vollkommen beschrieben.

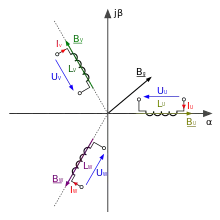
Betrachtet man Drehfeldmaschinen, so sind dort drei Spulen im Winkel von 120° angeordnet. In jeder dieser Spulen wird bei Stromfluss in der Maschine ein eigenes Magnetfeld erzeugt. Wird die Maschine nun an ein Drehstromsystem angeschlossen, ergibt sich für jeden Momentanwert jeweils eine andere Magnetisierung der Spulen. Da sich die drei Magnetfelder überlagern, ergibt sich im Luftspalt zwischen Stator und Rotor eine ungleichförmige magnetische Flussdichteverteilung. Die Verteilung der Flussdichte entlang des Umfangs des Luftspalts weist an einer bestimmten Stelle ein Maximum auf. Für jeden Momentanwert der Phasenströme hat die magnetische Flussdichte somit eine bestimmte Orientierung in der Maschine. Diese geometrische Orientierung kann nun durch die zwei Werte von Realteil und Imaginärteil als Raumzeiger dargestellt werden.

Berechnung des Raumzeigers

Allgemein kann der Raumzeiger aus den drei Einzelgrößen durch folgende Beziehung berechnet werden, wobei vorausgesetzt wird, dass das Koordinatensystem so angeordnet ist, dass die Wicklung U dieselbe Phasenlage wie die Realachse aufweist.

{\vec {B}}={\tfrac {2}{3}}\cdot (B_{U}+a\cdot B_{V}+a^{2}\cdot B_{W})

Wobei a und a² die Drehoperatoren darstellen.

a=e^{\mathrm {j} 120^{\circ }}=-{\tfrac {1}{2}}+\mathrm {j} {\tfrac {\sqrt {3}}{2}}

a^{2}=e^{-\mathrm {j} 120^{\circ }}=-{\tfrac {1}{2}}-\mathrm {j} {\tfrac {\sqrt {3}}{2}}

Da vorausgesetzt wird, dass die Nullbedingung erfüllt ist, wird durch die Raumzeigerdarstellung das dreiphasige Wicklungssystem durch ein zweiphasiges Wicklungssystem, bestehend aus zwei senkrecht zueinanderstehenden Wicklungen, ersetzt.

Die Darstellung als Raumzeiger ist nicht nur auf die magnetische Flussdichte beschränkt, sondern kann analog dazu für alle anderen elektrischen Größen wie Spannung, Strom und Fluss angewandt werden.

Koordinatensystem

Übersicht der Koordinatensysteme. Das rotorfeste dq-Koordinatensystem rotiert um das statorfeste αβ-Koordinatensystem.

Bei der vorhergehenden Betrachtung wurde davon ausgegangen, dass das Koordinatensystem ortsfest und mit dem Stator verbunden ist. Weiters wurde vorausgesetzt, dass die reelle Achse des Koordinatensystems mit der Wicklungsachse der U Wicklung zusammenfällt.

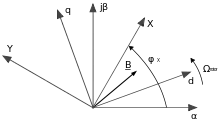
Der Raumzeiger muss jedoch nicht zwingend in dem bisher beschriebenen αβ-Koordinatensystem mit der Clarke-Transformation dargestellt werden. Für spezielle Anwendungen, wie beispielsweise die feldorientierte Regelung, ist es nötig, das Koordinatensystem mit dem Rotor der Drehfeldmaschine rotieren zu lassen. Das rotorfeste dq-Koordinatensystem rotiert somit mit der mechanischen Winkelgeschwindigkeit Ω_rotor um das statorfeste αβ-Koordinatensystem. Der Raumzeiger im dq-Koordinatensystem kann durch die dq0-Transformation aus den Phasengrößen berechnet werden.

Unabhängig davon kann genauso ein beliebiges Koordinatensystem, welches sich beispielsweise am Statorfluss, dem Luftspaltfluss oder dem Rotorfluss orientiert, gewählt werden.

Anwendung

Die Raumzeigerdarstellung findet vorwiegend in der elektrischen Antriebstechnik bei der Regelung von Drehfeldmaschinen Anwendung. Frequenzumrichter arbeiten zum Teil intern mit Raumzeigern, welche zur Steuerung der elektrischen Maschine mithilfe der Raumzeigermodulation ausgegeben werden.

Literatur

Dierk Schröder: Elektrische Antriebe – Grundlagen. 1. Auflage, Springer Berlin Heidelberg, Berlin, Heidelberg, 2009, ISBN 978-3-642-02989-9.
Joachim Specovius: Grundkurs Leistungselektronik. 2. Auflage, Vieweg, 2008, ISBN 978-3-8348-0229-3.

Weblinks

Theorie der Raumzeiger (PDF; 52 kB)
Studienarbeit zum Thema Raumzeiger

Siehe auch

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.