Prämisse

Als Prämisse (lat. praemissa „das Vorausgeschickte“) oder Vordersatz bezeichnet man in der Logik eine Voraussetzung oder Annahme. Sie ist eine Aussage, aus der eine logische Schlussfolgerung gezogen wird.

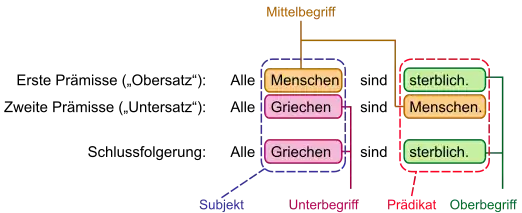
Beispiel aus Syllogismus

Beispiel:

Aus „Alle Menschen sind sterblich“

und „Alle Griechen sind Menschen“

folgt „Alle Griechen sind sterblich“.

Die beiden erstgenannten Aussagen sind dabei die Prämissen, die letztgenannte Aussage ist die Konklusion oder Schlussfolgerung.

Prämissen und Wahrheit

Sind die Prämissen in einem gültigen Schluss wahr, muss auch die Konklusion wahr sein. Ein Beispiel hierfür ist der obengenannte Schluss, dass aus „Alle Menschen sind sterblich“ und „Sokrates ist ein Mensch“ folgt „Sokrates ist sterblich“. Das Umgekehrte gilt jedoch nicht: Sind die Prämissen (oder einige der Prämissen) falsch, gilt nicht notwendigerweise, dass die Konklusion falsch ist. Beispielsweise folgt aus „Alle Menschen sind Griechen“ und „Sokrates ist ein Mensch“ der Satz „Sokrates ist Grieche“. Hier ist eine Prämisse falsch, dennoch ist die Konklusion wahr.

Prämissen brauchen also nicht unbedingt wahr zu sein. Im Gegenteil setzt man gelegentlich Prämissen, von denen man genau weiß, dass sie falsch sind. Dies ist z. B. bei der Beweistechnik des indirekten Beweises der Fall, bei welcher von einer falschen Annahme ausgegangen wird mit dem Ziel, diese zu widerlegen. Das vielleicht bekannteste Beispiel für einen indirekten Beweis ist der Satz des Euklid, bei dem bewiesen wird, dass es unendlich viele Primzahlen gibt.

Philosophiegeschichte

Der Terminus „Prämisse“ geht zurück auf die lateinische Übertragung der arabischen Literatur zur Aristotelischen Syllogistik im 12. Jahrhundert. „Prämisse“ ist dabei die Übersetzung des altgriechischen Wortes πρότασις (protasis, „Vorausgeschicktes“.[1]) „Prämisse“ werden hier beide Vordersätze eines Syllogismus genannt.[2]

Symbolische Darstellung

Symbolisch wird eine Schlussfolgerung wie folgt dargestellt:

\{\mathrm {A} _{1},\mathrm {A} _{2},\ldots ,\mathrm {A} _{n}\}\vdash \mathrm {B}

Lies: Aus $\mathrm {A} _{1},\mathrm {A} _{2},\ldots ,\mathrm {A} _{n}$ folgt $\mathrm {B}$ .

Eine Schlussfolgerung kann also mehrere Prämissen haben; man geht jedoch gewöhnlich davon aus, dass sie nur eine Konklusion hat. Dies ist aber im Grunde Konvention, es gibt keinen prinzipiellen Grund, warum eine Schlussfolgerung nicht mehrere Konklusionen haben sollte.

Abhängigkeit und Freiheit von Prämissen

Bei der oben dargestellten Schlussfolgerung spricht man davon, dass die Konklusion $\mathrm {B}$ aus den Prämissen $\mathrm {A} _{1},\mathrm {A} _{2},\ldots ,\mathrm {A} _{n}$ folgt. Dies bedeutet nicht, dass die Konklusion tatsächlich wahr ist oder gar immer wahr sein muss; ebenso wenig bedeutet es, dass die Konklusion nur dann wahr sein könnte, wenn die Prämissen wahr wären. Vielmehr bedeutet es lediglich, dass unter der Voraussetzung, dass alle Prämissen wahr sind, auch die Konklusion zwingend wahr ist.

In vielen logischen Systemen, so in der klassischen Aussagen- und Prädikatenlogik, gilt das Deduktionstheorem. Es sagt aus, dass es zulässig ist, eine der Prämissen in Gestalt des Vordersatzes einer „Wenn–dann“-Konstruktion (fachsprachlich materiale Implikation oder Konditional genannt) in die Konklusion zu verschieben, also vom Argument:

\{\mathrm {A} _{1},\mathrm {A} _{2},\ldots ,\mathrm {A} _{n}\}\vdash \mathrm {B}

überzugehen zum Argument:

\{\mathrm {A} _{1},\mathrm {A} _{2},\ldots ,\mathrm {A} _{n-1}\}\vdash \mathrm {A} _{n}\supset \mathrm {B}

Hierbei wurde die ehemalige Prämisse A_n zum Vordersatz, die ehemalige Konklusion B zum Nachsatz des Konditionals $\mathrm {A} _{n}\supset \mathrm {B}$ (lies: „Wenn A_n, dann B“), das die Konklusion des neuen Arguments bildet.

Auf dem Deduktionstheorem beruhen unter anderem die Kalküle des natürlichen Schließens.

Beispiel: Anstatt aus „Alle Menschen sind sterblich“ und „Sokrates ist ein Mensch“ zu folgern: „Sokrates ist sterblich“, kann man aus „Alle Menschen sind sterblich“ alleine folgern: „Wenn Sokrates ein Mensch ist, dann ist er sterblich“.

Eine andere Möglichkeit, die Zahl der Prämissen zu reduzieren, ohne die Gültigkeit des Arguments zu beeinträchtigen, ergibt sich, wenn es gelingt, eine der Prämissen aus den anderen herzuleiten, wenn also gilt:

\{\mathrm {A} _{1},\mathrm {A} _{2},\ldots ,\mathrm {A} _{n-1}\}\vdash \mathrm {A} _{n}

In diesem Fall ist die Prämisse $\mathrm {A} _{n}$ überflüssig (fachsprachlich: abhängig) und kann ebenfalls aus der Annahmenmenge getilgt werden.

Beispiel: Gelingt es, zu beweisen, dass Sokrates ein Mensch ist, so kann aus „Alle Menschen sind sterblich“ direkt gefolgert werden „Sokrates ist sterblich"“.

Siehe auch

Literatur

Gottfried Gabriel: Prämisse. In: Joachim Ritter u. a. (Hrsg.): Historisches Wörterbuch der Philosophie. Band 7, Schwabe, Basel 1972, Sp. 1255–1256

Weblinks

Wiktionary: Prämisse – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

Aristoteles, Topik I, 10.
Gottfried Gabriel: Prämisse. In: Joachim Ritter u. a. (Hrsg.): Historisches Wörterbuch der Philosophie. Band 7, Schwabe, Basel 1972, Sp. 1255–1256, hier: S. 1255.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Aristoteles, Topik I, 10.

[2] Gottfried Gabriel: Prämisse. In: Joachim Ritter u. a. (Hrsg.): Historisches Wörterbuch der Philosophie. Band 7, Schwabe, Basel 1972, Sp. 1255–1256, hier: S. 1255.