Spurkegel und Polkegel
Der Spurkegel und der Polkegel sind in der Kreiseltheorie Flächen, die von der Drehachse eines Kreisels mit Stützpunkt im Raum bzw. im Kreisel umfahren werden.[1] Beim symmetrischen Euler-Kreisel oder allgemeiner bei der regulären Präzession sind die Kegel wie geometrische Kreiskegel geformt,[2] was im Allgemeinen jedoch nicht der Fall ist. Die Spur- und Polkegel können beliebig gestaltet, offen oder unstetig sein, siehe auch die Animationen unten. Der Spurkegel wird auch Rastpolkegel oder Herpolhodiekegel und der Polkegel auch Gangpolkegel oder Polhodiekegel genannt (von altgriechisch πόλος pólos, „Achse“, ὁδός hodós, „Weg, Straße“, und ἕρπω hérpo, „kriechen“).
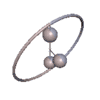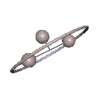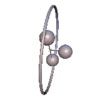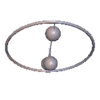 Pendelbewegung eines Gorjatschew-Tschaplygin-Kreisels
Pendelbewegung eines Gorjatschew-Tschaplygin-Kreisels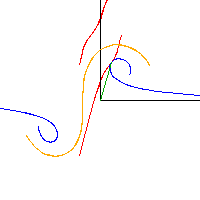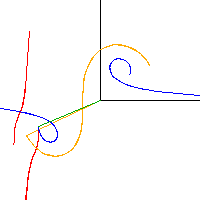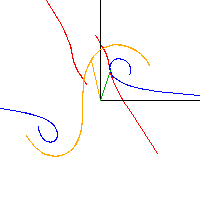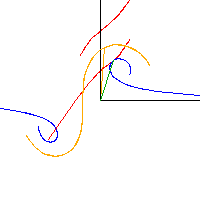 Schnitt durch den Spurkegel (blau) und Polkegel (rot) sowie 3-Achse (organge) und Drehachse (grün).
Schnitt durch den Spurkegel (blau) und Polkegel (rot) sowie 3-Achse (organge) und Drehachse (grün).
Die Berührungslinie von Spurkegel und Polkegel ist die momentane Drehachse, auf der alle Punkte des Kegels momentan stillstehen. Jede Bewegung des Kreisels mit Fixpunkt kann daher als Abrollen des körperfesten Polkegels auf dem raumfesten Spurkegel gedeutet werden.
Statt des Spur- und Polkegels kann auch die in ihnen enthaltene Bahnlinie des Endpunkts der Winkelgeschwindigkeit betrachtet werden. Die so entstehenden Spur- bzw. Polkurven rollen ebenfalls gleitungslos aufeinander ab. Der Abstand des Stützpunkts zu dem gemeinsamen Punkt der beiden Kurven zeigt hier zusätzlich die Geschwindigkeit des Abrollvorgangs an.[3]
Technisch ausgenutzt werden Spur- und Polkegel beim Kurvenkreisel und den Kollermühlen und Pendelmühlen.
Siehe auch
- Poinsotsche Konstruktion mit Polhodien und Herpolhodien, die der Pol- bzw. Spurkurve entsprechen.
- Rastpolbahn und Gangpolbahn, die aufeinander im Momentanpol abrollen, der bei einer ebenen Bewegung eines Starrkörpers der Ort seiner Drehachse ist.
Literatur
- K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 978-3-642-52163-8, S. 27 f. (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 20. Februar 2018]).
- R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Vieweg Verlag, Braunschweig 1920, DNB 451641280, S. 39 (archive.org – „Schwung“ bedeutet Drehimpuls und „Drehwucht“ Rotationsenergie).
Einzelnachweise
- Magnus (1971), S. 27 f., Grammel (1920), S. 40, siehe Literatur.
- Grammel (1920), S. 40.
- Magnus (1971), S. 28.