Poinsotsche Konstruktion

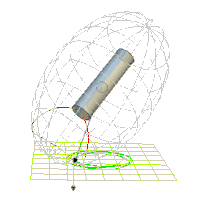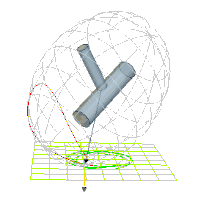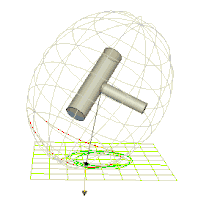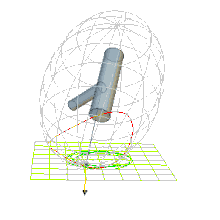
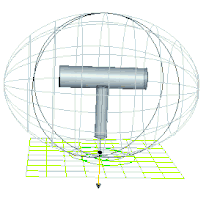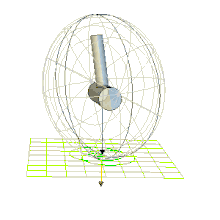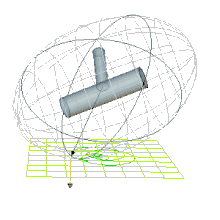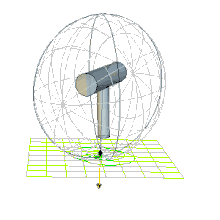
Die Poinsot’sche Konstruktion nach Louis Poinsot modelliert die Bewegung des kräftefreien Kreisels als gleitungsloses Abrollen des Energieellipsoids auf einer festen invariablen Ebene[1], siehe Abb. 1.

Abb. 1: Poinsot’sche Konstruktion

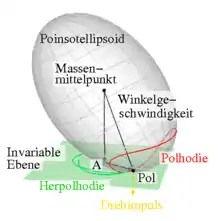
Die im Massenmittelpunkt aufgetragene Winkelgeschwindigkeit endet im Pol (griechisch πόλος pólos „Achse“). Dieser bewegt sich im körperfesten System auf geschlossenen Kurven, den Polhodien („Polpfade“ von ὁδός hodós „Weg, Pfad, Straße“), die auf dem Energieellipsoid oder Poinsotellipsoid liegen. Je nachdem, ob die Polhodien die Hauptträgheitsachse mit dem kleinsten oder dem größten Hauptträgheitsmoment umschließen, werden die Polhodien epi- bzw. perizykloidisch genannt. Die Polhodie im Abb. 1 ist epizykloidisch. Im raumfesten Inertialsystem berührt die Winkelgeschwindigkeit im Pol die invariable Ebene und zeichnet die Herpolhodien nach („Schlängelwege des Pols“ von ἕρπω hérpo „kriechen“). Die invariable Ebene tangiert jederzeit das Poinsotellipsoid.

Die genannten Elemente bilden die Poinsot’sche Konstruktion und ihr Zeitverlauf definiert die Poinsot’sche Bewegung. Durch die Poinsot’sche Konstruktion wird die Untersuchung der Drehbewegung von Starrkörpern zu einer geometrischen Aufgabe.

Animationen

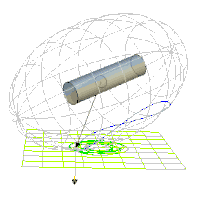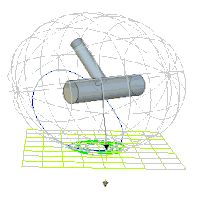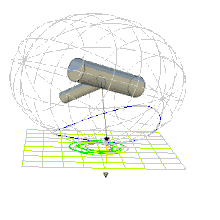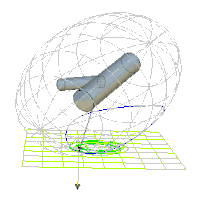
Epizykloidische Bewegung	Perizykloidische Bewegung	Bewegung nahe der Separatrix, siehe Dschanibekow-Effekt
Anders als in den Animationen dargestellt, bezieht sich der Drehimpuls jeweils auf den Massenmittelpunkt.

Beschreibung

Die Poinsot’sche Konstruktion betrachtet einen kräftefreien Kreisel, der in seinem Massenmittelpunkt ruht. Außer in der Schwerelosigkeit kann ein kräftefreier Körper in einem Schwerefeld realisiert werden, indem er in seinem Schwerpunkt drehbar, beispielsweise kardanisch aufgehängt wird.

Die Ausdehnung des Energieellipsoids ist konstant, da sie von der Rotationsenergie bestimmt wird, die beim kräftefreien Kreisel ein Integral seiner Bewegung ist, da mangels äußerer Kräfte keine Arbeit verrichtet wird. Dort, wo die aktuelle Winkelgeschwindigkeit das Energieellipsoid berührt, ist der aktuelle Drehimpuls senkrecht zu Tangentialebene. Der Drehimpuls ist beim kräftefreien Kreisel unveränderlich und somit sind die Tangentialebenen während der Bewegung parallel zueinander oder fallen zusammen.

Die Komponente der Winkelgeschwindigkeit in Richtung des Drehimpulses bleibt immer gleich. Denn bei der kräftefreien Drehbewegung eines Körpers ist sowohl seine Rotationsenergie E_rot als auch sein Drehimpuls ${\vec {L}}$ erhalten. Erstere berechnet sich aus letzterem durch skalare Multiplikation mit der Winkelgeschwindigkeit:

2E_{\text{rot}}={\vec {L}}\cdot {\vec {\omega }}=L\omega \cos \varphi \quad \rightarrow \quad \omega \cos \varphi ={\frac {2E_{\text{rot}}}{L}}

Darin ist L der Betrag des Drehimpulses, ω der Betrag der Drehgeschwindigkeit und φ der von Drehimpuls und Drehgeschwindigkeit eingeschlossene Winkel. Auf der rechten Seite der letzten Gleichung steht eine Konstante der Drehbewegung, weswegen die linke Seite, der Anteil der Winkelgeschwindigkeit in Richtung des Drehimpulses, ebenfalls konstant ist. Besagter Anteil bestimmt den Abstand der Tangentialebene vom Massenmittelpunkt. Dieser liegt im Ursprung O und sein Fußpunkt auf der Tangentialebene sei A. Dann ist dieser feste Anteil der Winkelgeschwindigkeit die Strecke OA. Somit ist die Tangentialebene an das Poinsotellipsoid im Pol fest und wird invariable Ebene genannt (grün Ebene in Abb. 1).

Trotzdem die Winkelgeschwindigkeit OA konstant ist, rotiert der Polstrahl AP nicht mit konstanter Drehgeschwindigkeit um die Achse OA, denn der Pol wandert nicht nur in der Ebene, sondern auch auf dem Poinsotellipsoid.[2]

Ein im Pol befindliches Partikel des Starrkörpers steht momentan still, denn es liegt auf der aktuellen Drehachse, die durch den ruhenden Massenmittelpunkt geht[3].

Wenn der Körper nicht um eine seiner Hauptträgheitsachsen kreist, dann kann von den Winkelgeschwindigkeiten ω_1,2,3 höchstens eine null sein. Die Euler’schen Kreiselgleichungen zeigen, dass von den Winkelbeschleunigungen dann niemals alle drei gleichzeitig verschwinden können. Der Pol bleibt demnach auf den Polhodien und Herpolhodien nicht stehen oder kehrt gar seine Bewegungsrichtung um.

Polhodien

Epi- und perizykloide Polhodien

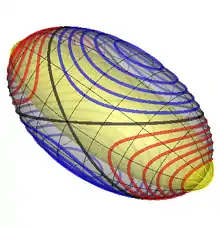
Abb. 2: Polhodien auf dem Poinsotellipsoid (grau) und Drallellipsoid (gelb).

Die Winkelgeschwindigkeit liegt zum Einen wegen der Energieerhaltung auf dem Poinsotellipsoid (grau in Abb. 2). Zum Anderen berührt sie wegen der Drehimpulserhaltung auch das Drallellipsoid, das im körperfesten System die Endpunkte aller Winkelgeschwindigkeitsvektoren enthält, die zum gleichen Drehimpulsbetragsquadrat führen (gelb). Die Polhodien sind die Schnittkurven dieser beiden Ellipsoide und sind als solche Kreis-, Ellipsen- oder Taco-förmige, geschlossene Kurven, die wie die Ellipsoide zu allen drei Hauptebenen, die von den Hauptträgheitsachsen erzeugt werden, symmetrisch sind. Die in Abb. 2 rot gezeichneten Polhodien, werden nach Arnold Sommerfeld und Felix Klein epizykloidische Polhodien genannt. Bei ihnen ist L² < 2Θ₂E_rot, worin E_rot die Rotationsenergie, L den Betrag des Drehimpulses und Θ₂ das mittelgroße Hauptträgheitsmoment bezeichnen. Die blau gezeichneten Kurven sind die perizykloidischen Polhodien, bei denen 2Θ₂E_rot < L² ist[4]. Zwischen den epi- und perizykloidischen Polhodien liegt die trennende Polhodie oder #Separatrix (schwarz), die bei L² = 2Θ₂ E_rot entsteht und aus zwei Ellipsen zusammengesetzt gedacht werden kann.

Berührungspunkte der Ellipsoide

Bei gegebener Rotationsenergie berührt das kleinstmögliche Drallellipsoid das Poinsotellipsoid an den Endpunkten der großen Achse. Diese Situation entspricht einer gleichförmigen Drehung um die Hauptträgheitsachse mit dem kleinsten Hauptträgheitsmoment, denn die Längen der Achsen sind umgekehrt proportional zu den Hauptträgheitsmomenten. Hier hat der Drehimpuls den minimalen mit der Rotationsenergie verträglichen Betrag. Wenn das größtmögliche Drallellipsoid das Poinsotellipsoid an den Endpunkten der kleinsten Achse berührt, findet eine gleichförmige Drehung um die Hauptträgheitsachse mit dem größten Hauptträgheitsmoment statt, und der Drehimpuls hat den maximalen, mit der Rotationsenergie verträglichen Betrag erreicht.[5]

Mathematisch drückt sich das so aus: Dreht der Körper mit der Winkelgeschwindigkeit ω_k um die k-te Hauptachse mit dem Hauptträgheitsmoment Θ_k, dann hat er den Drehimpuls L_k = Θ_kω_k und die Rotationsenergie

E_{\text{rot}}={\frac {1}{2}}\Theta _{k}\omega _{k}^{2}={\frac {L_{k}^{2}}{2\Theta _{k}}}\quad \rightarrow \quad L_{k}={\sqrt {2E_{\text{rot}}\Theta _{k}}}

Der Drehimpuls ist also betraglich am größten oder kleinsten, wenn der Körper um seine Hauptachse mit dem größten oder kleinsten Hauptträgheitsmoment dreht.

Rotierende und oszillierende Bewegungen

Auf den epizykloidischen Polhodien findet eine Drehung um die 1-Achse statt und der Drehwinkel um diese Achse ist unbeschränkt. Bei den perizykloidischen Polhodien schwankt der Drehwinkel um die 1-Achse zwischen zwei Extremwerten. Entsprechend werden die epizykloidischen Bewegungen als rotierend und die perizykloidischen als oszillierend bezeichnet.[6]

Stabilitätsbetrachtungen

Ist der Pol nur in der Nähe aber nicht auf der größten oder kleinsten Achse, verbleibt er auch in deren Nähe, denn die Polhodien umschließen diese Endpunkte. Das ist auf der Separatrix anders, wo ein in der Nähe aber nicht auf der mittleren Achse befindlicher Pol sich auf einer epi- oder perizykloidischen Polhodie erheblich von seiner Anfangslage entfernt und die Achse auch nicht umschlingt. Die größte und kleinste Achse markieren somit stabile Drehachsen, wohingegen die mittlere Drehachse eine instabile ist.

Bei stark abgeplatteten oder sehr schlanken Ellipsoiden kann bereits ein kleiner Stoß den Pol weit von der Hauptträgheitsachse wegführen, auch wenn die Bewegung um eine der stabilen Achsen stattfindet. Somit kann bei stark unterschiedlichen Hauptträgheitsmomenten auch eine stabile Drehachse instabil erscheinen. Ein Maß für die Stabilität der Drehachsen kann aus den Achsverhältnissen der Ellipsen abgeleitet werden, als welche die Polhodien bei Betrachtung aus Richtung der Hauptträgheitsachsen erscheinen. Die Winkelgeschwindigkeiten erfüllen die beiden Gleichungen

{\begin{aligned}2E_{\text{rot}}=&\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2}\\L^{2}=&\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}+\Theta _{3}^{2}\omega _{3}^{2}\,.\end{aligned}}

Projektion der Schnittkurven in Richtung einer der Hauptträgheitsachsen auf eine Ebene senkrecht dazu erfolgt durch Eliminierung der Winkelgeschwindigkeitskomponente in Richtung der Achse, was auf die Gleichungen

{\begin{aligned}L^{2}-2\Theta _{1}E_{\text{rot}}=&\Theta _{2}(\Theta _{2}-\Theta _{1})\omega _{2}^{2}+\Theta _{3}(\Theta _{3}-\Theta _{1})\omega _{3}^{2}\\2\Theta _{2}E_{\text{rot}}-L^{2}=&\Theta _{1}(\Theta _{2}-\Theta _{1})\omega _{1}^{2}+\Theta _{3}(\Theta _{2}-\Theta _{3})\omega _{3}^{2}\\2\Theta _{3}E_{\text{rot}}-L^{2}=&\Theta _{1}(\Theta _{3}-\Theta _{1})\omega _{1}^{2}+\Theta _{2}(\Theta _{3}-\Theta _{2})\omega _{2}^{2}\end{aligned}}

führt. Die erste und dritte Gleichung besitzen nur positive Koeffizienten, weswegen sie Ellipsen beschreiben, die die Achsverhältnisse

s_{1}={\sqrt {\frac {\Theta _{2}(\Theta _{2}-\Theta _{1})}{\Theta _{3}(\Theta _{3}-\Theta _{1})}}},\qquad s_{3}={\sqrt {\frac {\Theta _{2}(\Theta _{3}-\Theta _{2})}{\Theta _{1}(\Theta _{3}-\Theta _{1})}}}

aufweisen. Die Stabilität nimmt ab, je weiter sich die Verhältnisse von eins entfernen, und wird am größten, wenn der Kreisel symmetrisch bezüglich der 1- bzw. 3-Achse ist, denn dann wird s₁=1 bzw. s₃=1.[7]

Separatrix

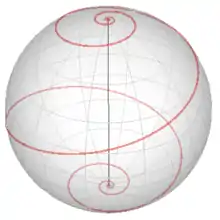
Abb. 3: Weg eines Punktes auf der 2-Achse (rot) um die Drehimpulsachse (senkrechte Linie) entlang einer Loxodrome

Auf der Separatrix ist L² = 2Θ₂E_rot und die zweite der obigen Ellipsengleichungen definiert gemäß

{\begin{aligned}2\Theta _{2}E_{\text{rot}}-L^{2}=0=&\Theta _{1}(\Theta _{2}-\Theta _{1})\omega _{1}^{2}+\Theta _{3}(\Theta _{2}-\Theta _{3})\omega _{3}^{2}\\\rightarrow \omega _{1}=&\pm {\sqrt {\frac {\Theta _{3}(\Theta _{3}-\Theta _{2})}{\Theta _{1}(\Theta _{2}-\Theta _{1})}}}\omega _{3}\end{aligned}}

zwei Ursprungsgeraden in der 1-3-Ebene. Die von diesen Geraden und der 2-Achse aufgespannten Ebenen enthalten die Separatrix, die als ebene Schnitte eines Ellipsoids aus Ellipsen besteht (schwarz in Abb. 2). Bei der Bewegung zeigt sich, dass sich ein Punkt auf der 2-Achse auf einer Loxodrome mit gleichmäßiger Drehgeschwindigkeit unendlich oft um die Drehimpulsachse dreht, siehe Abb. 3 und Bewegung auf der Separatrix. Der Pol nähert sich asymptotisch dem Schnittpunkt der beiden Ellipsen auf der 2-Achse an, erreicht sie aber nie.

Herpolhodien

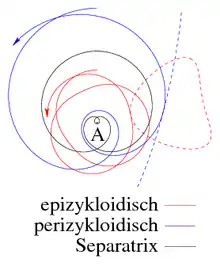
Abb. 4: Herpolhodien bei epi- und perizykloidischer Bewegung sowie Bewegung auf der Separatrix. Gestrichelt: in die invariable Ebene projizierte Polhodie zu einem Zeitpunkt.

Die Herpolhodien zeichnen den Weg des Pols in der invariablen Ebene nach. Weil der Anteil der Winkelgeschwindigkeit, der senkrecht zum Drehimpuls ist, der Polstrahl AP, wie die Winkelgeschwindigkeit selbst zwischen zwei Extremwerten schwankt, liegen die Herpolhodien zwischen zwei konzentrischen Kreisen um den Fußpunkt A des Massenmittelpunkts auf der invariablen Ebene, siehe Abb. 4. Die Herpolhodien sind wie in Abb. 4 meistens nicht geschlossen, wonach der Kreisel nicht mehr in seine Anfangslage zurückzukehren braucht. Trotz ihrer Benennung als Schlängelweg besitzen die Herpolhodien keine Wendepunkte und auch keine Spitzen. Der Krümmungsmittelpunkt liegt immer auf der Seite des Fußpunkts A.[4]

Beweis
Die Winkelgeschwindigkeit wird im körperfesten Hauptachsensystem ${\hat {g}}_{1,2,3}$ ausgedrückt und dient der Berechnung der Raten der Basisvektoren gemäß ${\vec {\omega }}=\sum _{i=1}^{3}\omega _{i}{\hat {g}}_{i}\quad {\text{und}}\quad {\dot {\hat {g}}}_{i}={\vec {\omega }}\times {\hat {g}}_{i}.$ Betrachtet werden Drehungen abseits der Hauptachsen, so dass von den Winkelgeschwindigkeiten ω_1,2,3 höchstens eine null sein soll. Die Geschwindigkeit des Pols ist ${\dot {\vec {\omega }}}$ und lautet: ${\dot {\vec {\omega }}}=\sum _{i=1}^{3}({\dot {\omega }}_{i}{\hat {g}}_{i}+\omega _{i}{\dot {\hat {g}}}_{i})=\sum _{i=1}^{3}({\dot {\omega }}_{i}{\hat {g}}_{i}+{\vec {\omega }}\times \omega _{i}{\hat {g}}_{i})=\sum _{i=1}^{3}{\dot {\omega }}_{i}{\hat {g}}_{i}.$ wegen ${\vec {\omega }}\times {\vec {\omega }}={\vec {0}}.$ Die Winkelbeschleunigungen ergeben sich aus den eulerschen Kreiselgleichungen: ${\begin{aligned}{\dot {\omega }}_{1}=&-{\frac {\Theta _{3}-\Theta _{2}}{\Theta _{1}}}\omega _{2}\omega _{3}=-p_{1}\omega _{2}\omega _{3}\quad {\text{mit}}\quad p_{1}:={\frac {\Theta _{3}-\Theta _{2}}{\Theta _{1}}}>0\\{\dot {\omega }}_{2}=&{\frac {\Theta _{3}-\Theta _{1}}{\Theta _{2}}}\omega _{3}\omega _{1}=p_{2}\omega _{1}\omega _{3}\quad {\text{mit}}\quad p_{2}:={\frac {\Theta _{3}-\Theta _{1}}{\Theta _{2}}}>0\\{\dot {\omega }}_{3}=&-{\frac {\Theta _{2}-\Theta _{1}}{\Theta _{3}}}\omega _{1}\omega _{2}=-p_{3}\omega _{1}\omega _{2}\quad {\text{mit}}\quad p_{3}:={\frac {\Theta _{2}-\Theta _{1}}{\Theta _{3}}}>0\end{aligned}}$ Weil nach Voraussetzung höchstens eine der Winkelgeschwindigkeiten null ist, können niemals alle drei Winkelbeschleunigungen gleichzeitig verschwinden, so dass der Pol niemals stehen bleiben kann und die Herpolhodien somit keine Spitzen aufweisen. Die Verhältnisse p_1,2,3 liegen alle im offenen Intervall (0,1), weil die Hauptträgheitsmomente die Dreiecksungleichungen erfüllen, und p₂ ist das größte, denn: ${\begin{aligned}p_{2}-p_{1}=&{\frac {\Theta _{3}-\Theta _{1}}{\Theta _{2}}}-{\frac {\Theta _{3}-\Theta _{2}}{\Theta _{1}}}={\frac {(\Theta _{2}-\Theta _{1})(\Theta _{1}+\Theta _{2}-\Theta _{3})}{\Theta _{1}\Theta _{2}}}>0\\p_{2}-p_{3}=&{\frac {\Theta _{3}-\Theta _{1}}{\Theta _{2}}}-{\frac {\Theta _{2}-\Theta _{1}}{\Theta _{3}}}={\frac {(\Theta _{3}-\Theta _{2})(\Theta _{2}+\Theta _{3}-\Theta _{1})}{\Theta _{2}\Theta _{3}}}>0.\end{aligned}}$ Die Beschleunigung des Pols ist ${\begin{aligned}{\ddot {\vec {\omega }}}=&\sum _{i=1}^{3}({\ddot {\omega }}_{i}{\hat {g}}_{i}+{\dot {\omega }}_{i}{\dot {\hat {g}}}_{i})=\sum _{i=1}^{3}({\ddot {\omega }}_{i}{\hat {g}}_{i}+{\vec {\omega }}\times {\dot {\omega }}_{i}{\hat {g}}_{i})=\sum _{i=1}^{3}{\ddot {\omega }}_{i}{\hat {g}}_{i}+{\vec {\omega }}\times {\dot {\vec {\omega }}}\end{aligned}}$ mit den Winkelrucken ${\begin{aligned}{\ddot {\omega }}_{1}=&-p_{1}({\dot {\omega }}_{2}\omega _{3}+\omega _{2}{\dot {\omega }}_{3})=p_{1}\omega _{1}(p_{3}\omega _{2}^{2}-p_{2}\omega _{3}^{2})\\{\ddot {\omega }}_{2}=&p_{2}({\dot {\omega }}_{3}\omega _{1}+\omega _{3}{\dot {\omega }}_{1})=-p_{2}\omega _{2}(p_{3}\omega _{1}^{2}+p_{1}\omega _{3}^{2})\\{\ddot {\omega }}_{3}=&-p_{3}({\dot {\omega }}_{1}\omega _{2}+\omega _{1}{\dot {\omega }}_{2})=p_{3}\omega _{3}(p_{1}\omega _{2}^{2}-p_{2}\omega _{1}^{2}).\end{aligned}}$ Nach elementaren Umformungen ergibt sich ${\ddot {\vec {\omega }}}={\begin{pmatrix}-\omega _{1}[p_{3}(1-p_{1})\omega _{2}^{2}+p_{2}(p_{1}+1)\omega _{3}^{2}]\\\omega _{2}[(p_{3}(1-p_{2})\omega _{1}^{2}-p_{1}(p_{2}+1)\omega _{3}^{2}]\\\omega _{3}[(p_{1}(p_{3}+1)\omega _{2}^{2}+p_{2}(1-p_{3})\omega _{1}^{2}]\end{pmatrix}}$ Die eckigen Klammern in der ersten und dritten Komponente sind positiv und weil nur höchstens eine der Winkelgeschwindigkeiten null sein soll, verschwindet die Polbeschleunigung nie. Das Kreuzprodukt mit der Polgeschwindigkeit liefert: ${\begin{aligned}{\dot {\vec {\omega }}}\times {\ddot {\vec {\omega }}}={\begin{pmatrix}\omega _{2}\omega _{3}[(p_{2}-p_{3})\omega _{1}^{2}+p_{1}(p_{2}+1)\omega _{3}^{2}+p_{1}(p_{3}+1)\omega _{2}^{2}]\\-\omega _{1}\omega _{3}[(p_{1}+p_{3})\omega _{2}^{2}+p_{2}(1-p_{3})\omega _{1}^{2}+p_{2}(p_{1}+1)\omega _{3}^{2}]\\\omega _{1}\omega _{2}[p_{3}(1-p_{1})\omega _{2}^{2}+p_{3}(1-p_{2})\omega _{1}^{2}+(p_{2}-p_{1})\omega _{3}^{2}]\end{pmatrix}}\end{aligned}}$ Das Kreuzprodukt verschwindet, wenn die Polbeschleunigung und -geschwindigkeit parallel sind und somit möglicherweise ein Wendepunkt in der Herpolhodie auftritt. Allerdings sind die eckigen Klammern sämtlich positiv, sodass nicht alle drei Komponenten auf einmal verschwinden können. Die Herpolhodien können also keinen Wendepunkt aufweisen.

Symmetrische Kreisel

Bei symmetrischen Kreiseln stimmen zwei Hauptträgheitsmomente überein, sodass das Poinsotellipsoid und das Drallellipsoid rotationssymmetrisch sind. Die Polhodien und die Herpolhodien werden dann zu Kreisen. Alle Winkelgeschwindigkeiten auf den Polhodien und auf den Herpolhodien bilden einen Kegel, den Spurkegel und Polkegel, die beim symmetrischen Kreisel Kreiskegel vorstellen. Der symmetrische, gestreckte, prolate Kreisel kann sich nur epizykloidisch, der symmetrische, abgeplattete, oblate Kreisel nur perizykloidisch bewegen. Wird beim prolaten Kreisel der Polhodienkreis in die invariable Ebene geklappt, so liegt er außerhalb des Herpolhodienkreises. Irgendein Punkt auf dem geklappten Polhodienkreis fährt beim Abrollen auf dem Herpolhodienkreis eine Epizykloide ab. Der in die invariable Ebene geklappte Polhodienkreis des oblaten Kreisels rollt hingegen innen auf dem Herpolhodienkreis ab, den der Polhodienkreis umschließt, und ein Punkt auf ihm zeichnet eine Perizykloide. Das motiviert die Bezeichnung der Bewegung als epi- bzw. perizykloidisch. Niemals kann der Fall eintreten, bei dem der rollende Polhodienkreis innerhalb des festen Herpolhodienkreises liegt und die Bewegung entsprechend hypozykloidisch heißen müsste.[8]

Lagrange-Kreisel

Die Poinsot’sche Konstruktion kann auch auf Lagrange-Kreisel übertragen werden. Der Lagrange-Kreisel ist ein symmetrischer schwerer Kreisel, bei dem der Massenmittelpunkt auf der Figurenachse liegt und der einen Stützpunkt hat. Bei schweren Kreiseln mit Stützpunkt bewegt sich der Drehimpuls in einer Ebene, die senkrecht zur Gewichtskraft ist, und der Abstand dieser Ebene vom Ursprung ist konstant, da es ein Integral der Bewegung ist. Da zwar die Gesamtenergie des Kreisels konstant ist, nicht so aber seine Rotationsenergie, hat das Poinsot-Ellipsoid eine Ausdehnung, die gegenläufig zur Lageenergie zu- und abnimmt. Die Polhodien liegen in einer Ebene, die senkrecht zur Figurenachse ist und den Abstand ω₃ vom Stützpunkt hat, denn die axiale Winkelgeschwindigkeit ω₃ ist beim Lagrange-Kreisel konstant.[9]

Allgemeiner Fall

Beim Lagrange-Kreisel sind die Herpolhodien im Allgemeinen sphärische Kurven, die also auf der Oberfläche einer Kugel verlaufen. Das Zentrum der Kugel liegt auf der Lotlinie im Abstand ${\tfrac {\Theta _{3}c_{0}}{(\Theta _{1}-\Theta _{3})L_{3}}}$ vom Stützpunkt und der Radius der Kugel hat die Länge[10]

r={\sqrt {{\frac {2E}{\Theta _{1}}}+{\frac {2\Theta _{3}c_{0}L_{z}}{\Theta _{1}(\Theta _{1}-\Theta _{3})L_{3}}}+{\frac {\Theta _{3}^{2}c_{0}^{2}}{(\Theta _{1}-\Theta _{3})^{2}L_{3}^{2}}}+\left({\frac {1}{\Theta _{3}}}-{\frac {1}{\Theta _{1}}}\right){\frac {L_{3}^{2}}{\Theta _{3}}}}}

Darin ist

Θ₁ das äquatoriale Massenträgheitsmoment,
Θ₃ das axiale Massenträgheitsmoment,
L_z der Drehimpuls um die Lotlinie,
L₃ der axiale Drehimpuls um die Figurenachse,
c₀ = mgs das Stützpunktmoment, gebildet aus der Gewichtskraft mg und dem Abstand s des Massenmittelpunkts vom Stützpunkt auf der Figurenachse, und
E ist die mechanische Gesamtenergie des Kreisels.

Der Abstand vom Stützpunkt zum Mittelpunkt der Kugel und ihr Radius wachsen über alle Grenzen, wenn Θ₁ = Θ₃, also beim Kugelkreisel, oder wenn L₃ = 0 und der Kreisel zum Pendel wird. Das über das Poinsot-Ellipsoid und die Polhodien gesagte bleibt in diesen Spezialfällen gültig.

Schwerer Kugelkreisel

Beim Kugelkreisel sind Winkelgeschwindigkeit und Drehimpuls proportional zueinander, weswegen sich auch die Winkelgeschwindigkeit in einer Ebene bewegt, die senkrecht zur Gewichtskraft ist.

Pendel

Beim Lagrange-Kreisel ohne axiale Winkelgeschwindigkeit ω₃ sind Winkelgeschwindigkeit und Drehimpuls auch proportional zueinander, weswegen das beim Kugelkreisel gesagte auch hier zutrifft. Ein Lagrange-Kreisel ohne axiale Winkelgeschwindigkeit ω₃ führt daher Pendelbewegungen[11] aus, bei denen sich der Endpunkt der Winkelgeschwindigkeit in einer horizontalen Ebene aufhält.

Einzelnachweise

Louis Poinsot: Théorie nouvelle de la rotation des corps. Bachelier, Paris 1834/1851, Grammel (1920), S. 24, Grammel (1950), S. 122 ff., Magnus (1971), S. 54, Leimanis (1965), S. 18, siehe Literatur.
Grammel (1920), S. 25
Grammel (1920), S. 24.
Grammel (1920), S. 36.
Grammel (1920), S. 35.
Léo Van Damme, Pavao Mardešić, Dominique Sugny: The tennis racket effect in a three-dimensional rigid body. 28. Juni 2016, abgerufen am 25. September 2016.
Grammel (1920), S. 39.
Grammel (1920), S. 41.
Klein und Sommerfeld (2010), S. 217.
Klein und Sommerfeld (2010), S. 236.
Klein und Sommerfeld (2010), S. 201.

Literatur

Louis Poinsot: Neue Theorie der Rotation von Körpern. Bachelier, Paris 1834 (französisch, archive.org – Originaltitel: Théorie nouvelle de la rotation des corps.).
R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Vieweg Verlag, Braunschweig 1920, DNB 573533210, S. 24, 32 (archive.org – "Schwung" bedeutet Drehimpuls, "Drehstoß" etwa Drehmoment und "Drehwucht" Rotationsenergie, siehe S. VII).
oder
R. Grammel: Der Kreisel. Theorie des Kreisels. 2. überarb. Auflage. Band 1. Springer, Berlin, Göttingen, Heidelberg 1950, DNB 451641299, S. 122 ff.
K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 978-3-642-52163-8, S. 53 ff. (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 7. Januar 2020]).
Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point. Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6, S. 18 ff., doi:10.1007/978-3-642-88412-2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 7. Januar 2020]).

Weblinks

Svetoslav Zabunov: Stereo 3D Rigid Body Simulation. Zabunov Laboratories, abgerufen am 11. Oktober 2016 (englisch, View auf „Poinsot construction (complete)“ einstellen).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Louis Poinsot: Théorie nouvelle de la rotation des corps. Bachelier, Paris 1834/1851, Grammel (1920), S. 24, Grammel (1950), S. 122 ff., Magnus (1971), S. 54, Leimanis (1965), S. 18, siehe Literatur.

[2] Grammel (1920), S. 25

[3] Grammel (1920), S. 24.

[grammel36-4] Grammel (1920), S. 36.

[5] Grammel (1920), S. 35.

[6] Léo Van Damme, Pavao Mardešić, Dominique Sugny: The tennis racket effect in a three-dimensional rigid body. 28. Juni 2016, abgerufen am 25. September 2016.

[7] Grammel (1920), S. 39.

[8] Grammel (1920), S. 41.

[9] Klein und Sommerfeld (2010), S. 217.

[10] Klein und Sommerfeld (2010), S. 236.

[11] Klein und Sommerfeld (2010), S. 201.