Gangpolbahn

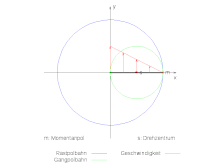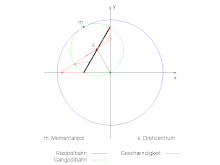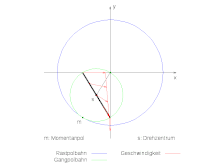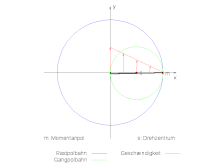
Bei einer ebenen Starrkörperbewegung ist der Momentanpol der Raumpunkt, in dem die Geschwindigkeit des dort befindlichen Partikels verschwindet und in dem sich die Bewegung momentan als reine Rotation darstellt. Die (körperfeste) Gangpolbahn (englisch : moving Centrode) bestimmt die Lage der Momentanpole in Abhängigkeit von der Zeit im körperfesten Bezugssystem, siehe Bild. Die Gangpolbahn ist die Kurve, auf der alle Partikel des Starrkörpers liegen, die bei der Bewegung jemals im Momentanpol zum Stehen kommen.

Animierte Kurbelschwinge:
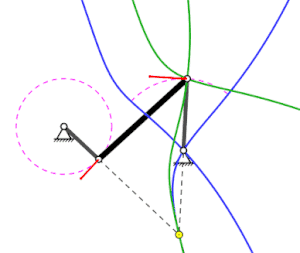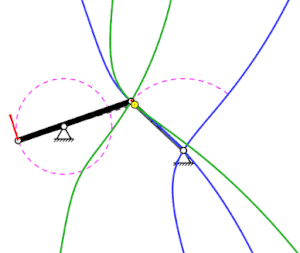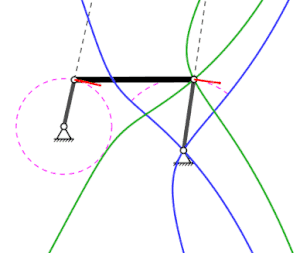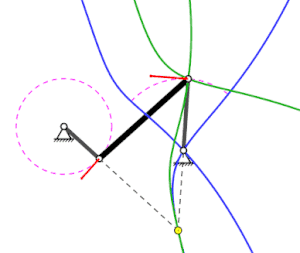
Rot: Geschwindigkeitsvektoren;
Gelber Punkt: Momentanpol;
Blau: Rastpolbahn des mittleren Stabes;
Grün: Gangpolbahn des mittleren Stabes

Für die Gangpolbahn gilt bei einer Bewegung in der x-y-Ebene und Drehung um die z-Achse:

{\begin{array}{rcl}x_{M}&=&{\frac {1}{\omega (t)}}[\sin(\varphi (t)){\dot {s}}_{x}(t)-\cos(\varphi (t)){\dot {s}}_{y}(t)]\\y_{M}&=&{\frac {1}{\omega (t)}}[\cos(\varphi (t)){\dot {s}}_{x}(t)+\sin(\varphi (t)){\dot {s}}_{y}(t)]\end{array}}

Der Index „M“ verweist auf den Momentanpol, (x, y) sind die Koordinaten in der Ebene, $({\dot {s}}_{x},{\dot {s}}_{y})$ die Geschwindigkeiten in x- bzw. y-Richtung des Bezugspunktes um den sich der Starrkörper dreht und $\varphi$ ist der Drehwinkel, dessen Zeitableitung die Winkelgeschwindigkeit ω um die z-Achse ist. Wenn ω=0 ist, dann liegt eine Translation vor und der Momentanpol und der ihm zugeordnete Punkt auf der Gangpolbahn ist nicht definiert. Die Gangpolbahn rollt gleitungslos auf der Rastpolbahn ab.

Die Gangpolbahn ist in der Kinematik von Fahrzeugen, Getriebetechnik, Robotik und auch Prothetik interessant.

Gangpolbahn in der komplexen Zahlenebene

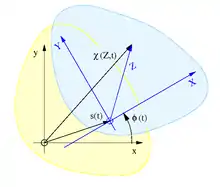
Rastebene (gelb) mit Rastkoordinaten (schwarz) und Gangebene (himmelblau) mit Gangkoordinaten (blau)

Der Momentanpol und die Gangpolbahn sind nur bei ebenen Bewegungen definiert und daher kann die ebene Starrkörperbewegung als Bewegung der komplexen Zahlenebene modelliert werden. Der feststehende Bildraum ist die Rastebene, die den Raum unserer Anschauung repräsentiert und die das Rastkoordinatensystem und die Rastpolbahn enthält. Der bewegte Urbildraum ist die Gangebene, die den in ihr ruhenden Starrkörper, das Gangkoordinatensystem und die Gangpolbahn beinhaltet. Alle Partikel des Starrkörpers bewegen sich synchron mit der Gangebene mit. In Anlehnung an die räumliche eulersche- und die materielle lagrangesche Betrachtungsweise werden die Koordinaten in der Rastebene als räumlich sowie mit Kleinbuchstaben und die Koordinaten in der Gangebene als materiell sowie mit Großbuchstaben bezeichnet, siehe Bild.

Jeder Punkt in der komplexen Zahlenebene entspricht einer komplexen Zahl. Die Translation eines Punktes wird mit der Addition einer anderen Zahl und die Rotation um den Ursprung mit dem Produkt mit der komplexen Zahl $e^{\mathrm {i} \varphi }$ modelliert, worin $\varphi$ der Drehwinkel, e die eulersche Zahl und i die imaginäre Einheit ist.

Die Bewegungsfunktion χ(Z,t) und Geschwindigkeit ${\dot {\chi }}(Z,t)$ eines Partikels Z kann dann in der Rastebene als

\chi (Z,t)=s(t)+e^{\mathrm {i} \varphi (t)}Z\quad \rightarrow \quad {\dot {\chi }}(Z,t)={\dot {s}}(t)+\mathrm {i} \omega (t)e^{\mathrm {i} \varphi (t)}Z

geschrieben werden. Der Punkt s(t) bezeichnet einen sich bewegenden Bezugspunkt, in dem der Ursprung des Gangkoordinatensystems liegt, und die Drehgeschwindigkeit ω ergibt sich aus der Zeitableitung des Drehwinkels: $\omega ={\dot {\varphi }}$ . Der Momentanpol steht in der Rastebene still, so dass

{\dot {s}}(t)+\mathrm {i} \omega (t)e^{\mathrm {i} \varphi (t)}M(t)=0\quad \rightarrow \quad M(t)=\mathrm {i} {\frac {e^{-\mathrm {i} \varphi (t)}}{\omega (t)}}{\dot {s}}(t)

folgt. Die materiellen Punkte M, deren Real- und Imaginärteil eingangs angegeben wurden, bezeichnen die Gangpolbahn in der Gangebene. Alle Partikel des Körpers, die jemals im Momentanpol stillstehen, liegen auf der Gangpolbahn. Die Rastpolbahn liefert hingegen Raumpunkte in der Rastebene, die irgendwann Momentanpol sind.

Abrollen der Gangpolbahn auf der Rastpolbahn

Bei der Bewegung des Starrkörpers rollt die Gangpolbahn gleitungslos auf der Rastpolbahn ab. Die Rast- und Gangpolbahn sind mit der Zeit t parametrisiert. Weil dies nun bekannt ist, wird auf die Angabe des Zeitparameters der Übersichtlichkeit halber verzichtet. Die Polwechselgeschwindigkeit auf der Rastpolbahn $m=s+{\frac {\mathrm {i} }{\omega }}{\dot {s}}$ lautet in der Rastebene:

{\dot {m}}={\dot {s}}-{\frac {\mathrm {i} }{\omega ^{2}}}{\dot {\omega }}{\dot {s}}+{\frac {\mathrm {i} }{\omega }}{\ddot {s}}\,.

Die Polwechselgeschwindigkeit ${\dot {M}}$ auf der Gangpolbahn überträgt sich mit der Bewegungsfunktion $\chi (M,t)=s+Me^{\mathrm {i} \varphi }$ in die Rastebene:

{\begin{array}{rcl}{\dfrac {\mathrm {d} }{\mathrm {d} t}}\chi (M(t),t)&=&{\dfrac {\partial }{\partial M}}\chi (M,t){\dot {M}}+\overbrace {{\dfrac {\partial }{\partial t}}\chi (M,t)} ^{=v|_{M=const}=0}={\dot {M}}e^{\mathrm {i} \varphi }\\[2ex]&=&{\frac {\mathrm {d} }{\mathrm {d} t}}\left(\mathrm {i} {\frac {e^{-\mathrm {i} \varphi }}{\omega }}{\dot {s}}\right)e^{\mathrm {i} \varphi }=\left(\mathrm {i} (-\mathrm {i} \omega ){\frac {e^{-\mathrm {i} \varphi }}{\omega }}{\dot {s}}-\mathrm {i} {\frac {e^{-\mathrm {i} \varphi }}{\omega ^{2}}}{\dot {\omega }}{\dot {s}}+\mathrm {i} {\frac {e^{-\mathrm {i} \varphi }}{\omega }}{\ddot {s}}\right)e^{\mathrm {i} \varphi }={\dot {m}}\end{array}}

In der Rastebene sind die Polwechselgeschwindigkeiten also auf der Rastpolbahn und Gangpolbahn in Betrag und Richtung gleich, weswegen die beiden Kurven gleitungslos aufeinander abrollen.

Beispiel

Rastpol- und Gangpolbahn bei einem rechtwinkligen Kreuzschieber (Animation 1,6 M)

Die grün eingefärbte Gangpolbahn des rechts im Bild gegebenen Systems soll berechnet werden. Der Mittelpunkt S des Kreuzschiebers bewege sich mit der konstanten Winkelgeschwindigkeit Ω auf der nicht eingezeichneten Kreisbahn mit dem Radius R um den Ursprung. In der komplexen Zahlenebene lautet der Bezugspunkt $s=Re^{\mathrm {i} \Omega t}$ und der um den Bezugspunkt laufende Punkt auf dem Kreuzschieber rotiert mit der entgegengesetzten Winkelgeschwindigkeit ω=-Ω. So ergibt sich für den Momentanpol:

M={\frac {\mathrm {i} e^{-\mathrm {i} \varphi (t)}}{\omega (t)}}{\dot {s}}(t)={\frac {\mathrm {i} e^{-\mathrm {i} (-\Omega t)}}{-\Omega }}\mathrm {i} \Omega Re^{\mathrm {i} \Omega t}=Re^{2\mathrm {i} \Omega t}

d. h. der Radius der grün eingefärbten Gangpolkurve ist gleich der halben Länge des fett schwarz modellierten Kreuschiebers und damit gleich dem Radius der kreisförmigen Bahn des Punktes S. Der Radius der blau eingefärbten Rastpolkurve ist gleich dem doppelten Radius der Gangpolkurve und damit identisch mit der Länge des Kreuzschiebers.

Punktweises Ermitteln der Gangpolkurve

Ermittlung der Gangpolkurve einer umlauffähigen Doppelkurbel

Heutzutage werden häufig CAD-Systeme zur Simulation von Starrkörpersystemen eingesetzt, die punktweises Konstruieren von Bahnen ermöglichen. CAD-Systeme ermöglichen somit die leichte Umsetzung der Zeichnungsfolge-Rechenmethode mit geringen mathematischen Kenntnissen und gleichzeitig erlaubt diese Methode dem Anwender, die entstandenen Ergebnisse leicht nachzuprüfen

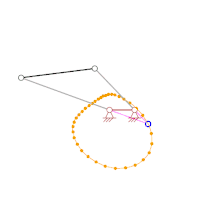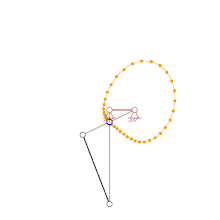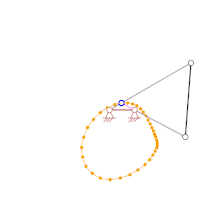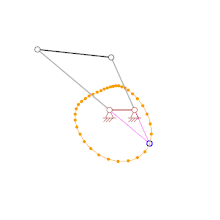
Wie aus dem Bild der animierten Kurbelschwinge (ganz oben) hervorgeht, liegt der Momentanpol immer auf der Senkrechten zum Geschwindigkeitsvektor eines Partikels des Starrkörpers und somit auf der Normalen zur Bahn des Partikels. Der Momentanpol liegt also im Schnittpunkt der Normalen zu den Bahnen von 2 Partikel. Die Gangpolbahn ergibt sich durch das Verbinden der Momentanpole.

Bei viergliedrigen Gelenkgetrieben wie z. B. Doppelkurbeln lässt sich die Gangpolbahn der rechts im Bild schwarz dargestellten Koppel besonders einfach punktweise ermitteln, da die Bahn der Gelenke der Koppel jeweils einen Kreisbogen mit dem Gestellgelenk als Mittelpunkt bilden (vergleiche Bild ganz oben) und somit die Normalen mit der Richtung der grauen Kurbeln bzw. Schwingen identisch sind. Bei viergliedrigen Gelenkgetrieben liegen die Momentanpole demnach immer im Schnittpunkt der grauen Kurbeln oder Schwingen bzw. im Schnittpunkt deren violetten Verlängerungen.

Siehe auch

Literatur

M. Husty: Kinematik und Robotik. Springer, 2012, ISBN 978-3-642-63822-0.
K. Luck, K.-H. Modler: Getriebetechnik: Analyse Synthese Optimierung. Springer, 1990, ISBN 978-3-211-82147-3.
G. Bär: Ebene Kinematik. Script zur Vorlesung. Institut für Geometrie, TU Dresden (tu-dresden.de [PDF; abgerufen am 1. April 2015] Enthält weitere Literaturempfehlungen).

Weblink

Commons: Rast- und Gangpolbahnen – Sammlung von Bildern, Videos und Audiodateien

Lehrbuch der Technischen Mechanik – Dynamik: Eine anschauliche Einführung in der Google-Buchsuche

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.