Sinuslauf
Der Sinuslauf, auch Wellenlauf genannt, tritt auf bei Rad-Schiene-Systemen mit konisch profilierten, also sich nach außen hin verjüngenden, starr gekoppelten Rädern. Zweck der Konizität ist die Selbstzentrierung des Radsatzes im geraden Gleis ohne Benutzung der Spurkränze.[1]
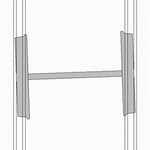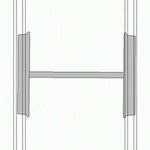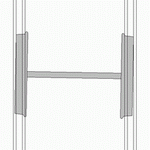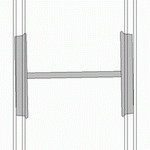
Diese Bewegung ist bei kleinen Amplituden sinusförmig und hat eine konstante Wellenlänge, also eine mit der Fahrgeschwindigkeit zunehmende Frequenz. Sie wird bei hoher Geschwindigkeit durch dynamische Kräfte angefacht (engl. hunting oscillation) bis hin zum Zick-Zack-Lauf mit Anschlag der Spurkränze an die Schienen, sodass Maßnahmen zur Dämpfung getroffen werden müssen, um übermäßigen Verschleiß und Komforteinbußen durch Vibrationen zu vermeiden.
Beim Talgo sind die beiden Räder einer Achse nicht miteinander gekoppelt, so dass dieses Prinzip der Selbstzentrierung nicht anwendbar ist.
Sinusförmiger Rollweg
Bei einem Radsatz mit konischem Radprofil, der außermittig auf zwei parallelen Schienen steht, sind die Radien der beiden Räder an den Berührpunkten mit den Schienen unterschiedlich groß. Da die beiden Räder über die Radsatzwelle starr verbunden sind und gleich schnell drehen, vollführt das Rad mit dem größeren Radius am Berührpunkt einen längeren Weg nach vorne als das Rad mit dem kleineren Radius. Daher lenkt ein zu weit rechts stehender Radsatz nach links und umgekehrt. Hierdurch kommt es zu einer Schlingerbewegung, die sich in einer nichtlinearen Differenzialgleichung darstellen lässt. Im Grenzfall kleiner Amplituden, also bei Linearisierung, ergibt sich als Lösung eine Sinuskurve. Die Formel wurde 1883 von Johannes Klingel veröffentlicht. Sofern keine äußeren Anregungen durch Kurven oder Ungenauigkeiten der Gleisverlegung vorliegen, sollte diese Schwingung gedämpft werden und abklingen.
In der Realität sind die Profile durch Verschleiß nicht exakt konisch oder werden gleich als Verschleißprofil angelegt, um eine starke Änderung des Laufverhaltens durch Verschleiß des Rad- und des Schienenprofils zu vermeiden. Das führt in Verbindung mit der oben vernachlässigten endlichen Krümmung des Schienenprofils zu einer nichtlinearen Abhängigkeit des Abrollradius vom seitlichen Versatz. Sofern die Berührpunkte bei Änderung des Versatzes nicht springen, kann diese Abhängigkeit für kleine Auslenkungen linear genähert werden, siehe Äquivalente Konizität, sodass obige Herleitung ihre Gültigkeit behält. Bei größeren Auslenkungen führt die nichtlineare Zunahme der Rollradiendifferenz beim Anlauf an den Spurkranz sowie die daraus resultierenden vertikalen Kräfte zu einer zwangsweisen Führung das Radsatzes im Gleis, selbst bei instabilem Verhalten.
Dynamische Stabilität
Die Reibung zwischen Rad und Schiene, insbesondere bei starrer Kopplung zweier Radsätze in einem Drehgestell, dämpft die Schwingung und stabilisiert einen ruhigen Lauf, während mit zunehmender Geschwindigkeit die Anregung der Schwingung stärker wird. Überwiegt die Dämpfung, so kehrt ein Radsatz, der durch einen Fehler in der Gleislage oder durch eine Kurve in eine außermittige Lage geraten ist, nach einigen Perioden wieder in die mittige Lage zurück (gedämpftes Verhalten). Überwiegt dagegen die Anregung, so nimmt die Amplitude zu, bis sie durch erhöhte nichtlineare Kräfte an den Spurkränzen begrenzt wird. Die bei hoher Geschwindigkeit großen Rückstellkräfte stören die Fahrgäste durch Vibrationen und Lärm, belasten das Fahrzeug und den Gleisoberbau und müssen daher konstruktiv vermieden werden.
Ein Radsatzpaar in einem Drehgestell erreicht einen ungestörten Lauf bis 180 km/h; für höhere Geschwindigkeiten kann das Radprofil flacher gewählt (siehe Äquivalente Konizität) und die Gierbewegung des Drehgestells gegen den Wagenkasten zusätzlich gedämpft werden (z. B. Drehdämpfer am Drehgestell MD 36 oder Hartmanganplatten am Drehgestell MD 522). Durch entsprechende Auslegungen der Profile, der Steifigkeit innerhalb des Drehgestells und der Drehdämpfung kann stabiles Verhalten bei sehr hohen Geschwindigkeiten erreicht werden.[2] Beispiele hierfür sind der InterCityExperimental auf dem Rollenprüfstand München-Freimann mit 500 km/h (1982) bzw. auf freier Strecke mit 407 km/h (1988)[3] sowie der französische TGV mit einer Rekordgeschwindigkeit von 574 km/h (2007). Für den deutschen ICE der Serie 1 wurde aufgrund der Versuchsergebnisse und der Herstellkosten das Drehgestell MD 52-530 der Waggon Union ausgewählt.
Praxiseinwirkungen
Zu einem exakt sinusförmigen Lauf kommt es nur im vereinfachten Modell; der tatsächliche Laufweg wird auch davon beeinflusst, dass ein normaler Radsatz in der Regel keine exakt konischen Radprofile hat und auch die für das Kegel- und Spurkranz-System optimierte Schienenprofilform nicht an allen Stellen exakt verläuft, sowie ungeregelte Kräfte, die vom Drehgestell bzw. dem Wagenkasten eingeleitet werden. Dennoch lässt sich der Lauf von Radsätzen technisch so exakt dämpfen, dass nur noch Taumelbewegungen im Millimeterbereich auftreten. Damit wird ein besseres Laufverhalten und ein geringerer Verschleiß erreicht als bei Radsätzen mit zylindrischem Radprofil.
Die zulässige Höchstgeschwindigkeit von konventionellen Schienenfahrzeugen wird durch die präzise Abstimmung von Rad- und Schienenprofil und die Gewährleistung der ständigen Überwachung und Nachbesserung maßgeblich mitbestimmt.
Bei Gleisverläufen mit vielen engen Radien kommen die Vorteile eines konischen Radprofils mit Sinuslauf kaum zum Tragen. Das Einschwingen eines stabilen Sinuslaufes benötigt eine gewisse ungestörte Weglänge, diese ist bei Stadtbahnsystemen in der Regel nicht gegeben.
Literatur
- Klaus Knothe, Sebastian Stichel: Schienenfahrzeugdynamik, 2003, ISBN 3540434291
- Rainer Kratochwille: Zum Nutzen schaltbarer Schlingerdämpfer …, Dissertation 2004
Einzelnachweise
- Jörn Pachl: Systemtechnik des Schienenverkehrs, Springer Vieweg, 2018, Seite 24
- Peter Meinke, A. Mielcarek: Design and Evaluation of Trucks for High-Speed Wheel/Rail Application. Hrsg.: International Centre for Mechanical Sciences. Band 274. Springer, Wien 1982, S. 281–331 (englisch).
- Peter Meinke, Lutz Mauer: Laufdrehgestell für den Hochgeschwindigkeitsbereich. In: Eisenbahntechnische Rundschau, Lauftechnik und Laufwerke von Schienenfahrzeugen. Band 37, Nr. 12, 1988, S. 791–798.