Shannon-Hartley-Gesetz

Das Shannon-Hartley-Gesetz beschreibt in der Nachrichtentechnik die theoretische Obergrenze der Bitrate eines Übertragungskanals in Abhängigkeit von Bandbreite und Signal-zu-Rausch-Verhältnis, über den mit einer gewissen Wahrscheinlichkeit eine fehlerfreie Datenübertragung möglich ist. Es ist nach Claude Elwood Shannon und Ralph Hartley benannt.[1][2]

In der Praxis wird die erzielbare Bitrate von Eigenschaften wie der Kanalkapazität und von Verfahren wie der Kanalkodierung beeinflusst. Das Shannon-Hartley-Gesetz liefert das theoretische Maximum, das mit einer hypothetischen optimalen Kanalkodierung erreichbar ist, ohne darüber Auskunft zu geben, mit welchem Verfahren dieses Optimum zu erreichen ist.

Einführung

Über einen perfekten (d. h. störungsfreien) Übertragungskanal könnte man theoretisch Daten in unbegrenzter Menge übertragen. Da aber real existierende Kanäle sowohl in ihrer Bandbreite begrenzt als auch Störungen wie Einstreuungen, thermischem Rauschen, endlichem Widerstand des Leiters usw. unterworfen sind, ist die maximal mögliche Übertragungsrate begrenzt. Die Übertragungsrate wird durch beide Faktoren begrenzt:

Die Bandbreite des Übertragungsweges bestimmt die maximal mögliche Symbolrate, also wie viele einzelne Symbole pro Zeiteinheit sicher übertragen werden können.
Die Stärke der auf dem Übertragungsweg entstandenen bzw. eingefangenen Störungen, beschrieben durch das Signal-Rausch-Verhältnis, begrenzt den maximalen Informationsgehalt eines Symbols, d. h., wie viele unterschiedliche Symbole am Empfänger noch sicher unterschieden werden können.

Vereinfachend gesagt bestimmt die Bandbreite, wie oft bei der Übertragung durch ein Kabel die Spannung pro Zeiteinheit geändert werden kann, und das Signal-Rausch-Verhältnis, wie viele verschiedene Spannungspegel dabei beim Empfänger noch sicher unterschieden werden können.

Präziser drückt das Shannon-Hartley-Gesetz den Umstand aus, dass bei einem durch Störungen wie Rauschen gestörten Übertragungskanal eine mittels Kanalcodierung erzielbare fehlerfreie Datenübertragung mit einer Wahrscheinlichkeit von δ > 0 möglich ist, wenn die realisierte Bitrate C_R kleiner als die durch das Shannon-Hartley-Gesetz gebildete Grenze C_S ist. Es wird als Besonderheit dabei keine Aussage getroffen, mit welcher konkreten Kanalcodierung oder welchem technischen Verfahren dieser Fall erreicht werden kann. Liegt die realisierte Bitrate C_R über der Grenze von C_S, beträgt die Wahrscheinlichkeit für Fehlerfreiheit δ = 0, was bedeutet, dass unabhängig von den eingesetzten Verfahren keine fehlerfreie Datenübertragung möglich ist.

Mathematische Beschreibung

Rauschfreier Übertragungskanal

Die maximale Datenübertragungsrate C_N bei einem störungsfreien Übertragungskanal mit der Bandbreite B ist gegeben durch:

C_{N}=2\cdot B

Die Bandbreite B wird in Hertz angegeben, die Datenübertragungsrate in Symbole pro Sekunde (Baud).

Bei binärem Symbolalphabet mit nur zwei Zeichen ist die Bitrate, gemessen in bit/s (bps), gleich der Symbolrate, gemessen in Baud. Stehen L Symbole zur Verfügung, lassen sich ld(L) Bits pro Symbol darstellen:

C_{N}=2\cdot B\cdot \mathrm {ld} (L),

wobei der Ausdruck ld(·) den Logarithmus zur Basis 2 bezeichnet.

Beispiel: Bei einer Bandbreite von 1000 Hz können maximal 2000 baud übertragen werden. Bestehen die Symbole aus einem Bit, z. B. „0“ oder „1“, erreicht man eine Datenrate von 2000 bit/s. Handelt es sich um 26 Zeichen des deutschen Alphabets (ohne Sonderzeichen), ist die Datenrate mit 9400 bit/s um den Faktor ld(26) größer. Durch Wahl hinreichend vieler unterschiedlicher Symbole kann auf einem rauschfreien, bandbegrenzten Übertragungskanal eine beliebig hohe Bitrate erzielt werden.

Übertragungskanal mit Rauschen

Claude Shannon verallgemeinerte dieses Theorem. Für einen mit additivem weißem gaußschem Rauschen gestörten Kanal, abgekürzt AWGN-Kanal, nimmt das Shannon-Hartley-Gesetz folgende Form an:

C_{S}=B\cdot \mathrm {ld} \left(1+{\frac {S}{N}}\right)=B\cdot \mathrm {ld} \left(1+{\frac {S}{N_{0}\cdot B}}\right)

C_S stellt die (bei diesem Kanalmodell) maximal mögliche Bitrate (Bits pro Sekunde) dar, S die Signalleistung. Der Parameter N stellt die spektral konstante Rauschleistung dar, das Verhältnis S/N wird auch als Signal-Rausch-Verhältnis (SNR) bezeichnet. Die Rauschleistung N kann auch durch die Energie der Rauschleistungsdichte N₀ über die Bandbreite B ausgedrückt werden.

Die maximal mögliche Bitrate stellt eine obere Grenze unter der Voraussetzung von weißem Rauschen dar. Bei Kanalmodellen, die nicht dem AWGN-Kanal entsprechen, wie auch bei unterschiedlichen spektralen Rauschleistungsdichten ergeben sich andere Zusammenhänge.

Beispiel: Über eine Leitung mit dem SNR von 20 dB lassen sich bei einer verfügbaren Bandbreite von 1000 Hz maximal 6,7 kbit/s übertragen.

Rechnung:

Umwandlung von SNR in S/N: SNR = 10·log₁₀(S/N) → 20 dB = 10·log₁₀(x) ↔ 2 dB = log₁₀(x) ↔ 10² = x ↔ x = 100 → S/N = 100
Berechnung der Übertragungskapazität: C_S = f_max·log₂(1+S/N) = 1000 Hz·ln(1+100)÷ln(2) bit = 1000·ln(101)÷ln(2) bit/s ≈ 6658 bit/s ≈ 6,7 kbit/s

Diese Bitrate lässt sich beispielsweise durch entsprechende Kanalcodierung wie den Turbo-Codes annähernd in der Praxis erreichen.

Weitere Werte zur Abschätzung bei einer Bandbreite von B=1 Hz (Werte gerundet):

SNR	C_s	SNR	C_s	SNR	C_s
–30 dB	0,001442 bit/s	0 dB	1,000 bit/s	+20 dB	6,658 bit/s
–20 dB	0,014355 bit/s	+3 dB	1,582 bit/s	+40 dB	13,288 bit/s
–10 dB	0,137503 bit/s	+6 dB	2,316 bit/s	+60 dB	19,932 bit/s
–6 dB	0,323299 bit/s	+10 dB	3,459 bit/s	+80 dB	26,575 bit/s
–3 dB	0,586104 bit/s	+15 dB	5,028 bit/s	+100 dB	33,219 bit/s

Grenzen

Bitfehlerhäufigkeit als Funktion von E_b/N₀

Wird bei konstant gehaltener Signalleistung S und konstanter spektraler Rauschleistungsdichte N₀ nur die Bandbreite B erhöht, lässt sich die maximal mögliche Bitrate C_S bis auf

\lim _{B\to \infty }C_{S}={\frac {S}{N_{0}}}\mathrm {ld} (e)\approx 1{,}442\dots {\frac {S}{N_{0}}}

steigern. Dies bedeutet, dass sich auch durch eine gegen unendlich ausgedehnte Bandbreite B des Übertragungskanals die maximal mögliche Bitrate nur begrenzt steigern lässt.

In realen Übertragungssystemen lässt sich auch die Energie E_b, die zur Übertragung von einem Bit aufgewendet werden muss, variieren. Zur Übertragung erfordert dies eine Signalleistung S für die Dauer T. Die tatsächliche Bitrate C_R liegt immer unter der maximal möglichen Bitrate C_S:

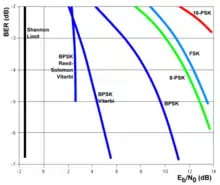
{\frac {C_{R}}{B}}=x<{\frac {C_{S}}{B}}=\mathrm {ld} \left(1+{\frac {S}{N_{0}\cdot B}}\right)=\mathrm {ld} \left(1+{\frac {C_{R}}{B}}\cdot {\frac {E_{b}}{N_{0}}}\right)

Diese Gleichung beschreibt die Shannon-Grenze (engl. Shannon limit) als Funktion von E_b/N₀: x(E_b/N₀). Die Relation C_R/B = x beschreibt, wie viele bit/s pro Hertz Bandbreite mit einer bestimmten Übertragungstechnik in Abhängigkeit vom SNR übertragen werden können, und wird als die spektrale Effizienz bezeichnet. In der rechten Darstellung sind die Verläufe von unterschiedlichen Übertragungsverfahren mit Farben blau, rot und grün dargestellt.

Als Grenzfall bei Gleichsetzung der obigen Ungleichung und wenn die spektrale Effizienz gegen 0 bit/s pro Hz Bandbreite geht, ergibt sich nach Umformen das untere Limit des SNR zu:

{\frac {E_{b}}{N_{0}}}=\lim _{x\to 0}{\frac {2^{x}-1}{x}}=\ln(2)\approx 0{,}693\approx -1{,}6\,\mathrm {dB}

Dies drückt den Umstand aus, dass unter einem Verhältnis von E_b/N₀ = −1,6 dB in einem AWGN-Kanal keine fehlerfreie Datenübertragung möglich ist. Bei diesem Verhältnis handelt es sich nicht um das S/N, sondern um die Energie E_b, die zur Übertragung der Informationsmenge von einem Bit bei spektraler Rauschleistungsdichte N₀ minimal aufgewendet werden muss. Sie ist im rechts dargestellten Diagramm für die Verhältnisse von E_b/N₀ bei verschiedenen Kanalcodierungen als senkrechte schwarze Grenzlinie eingezeichnet.[3]

Jener Grenzwert gilt für kleine spektrale Effizienz mit x ≪ 1. Solche Signale werden auch als leistungsbegrenzte Signale bezeichnet, in denen die Bandbreite groß, aber die zur Verfügung stehende Leistung limitiert ist. Beispielsweise ist die Kommunikation zu Raumsonden leistungsbegrenzt, während die Abstrahlung auf einem großen Frequenzband erfolgt. Dieser Abschnitt der Shannon-Grenze ist in der rechten Abbildung in der Farbe Schwarz dargestellt.

Für die spektrale Effizienz x ≫ 1 ist hingegen die Bandbreite B der limitierende Faktor, diese Signale werden als bandbegrenzte Signale bezeichnet. Beispielsweise sind terrestrische digitale Funkverbindungen mit spektral effizienten Modulationsverfahren wie 1024-QAM typische bandbreitenbegrenzte Signale.

Shannons geometrisch-stochastischer Ansatz

In der Arbeit „Communication in the presence of noise“ modellierte Claude Elwood Shannon den Übertragungskanal als reellen Vektorraum. Jedes übertragbare Symbol ist eine Koordinate in diesem Vektorraum. Da in der Zeit beliebig viele Symbole übertragen werden können, ist der Vektorraum unendlichdimensional. Jeder Koordinate entspricht ein Basissignal, d. h. eine reellwertige, von der Zeit abhängige Funktion. Der Einfachheit des Modells halber sollen sich die Basissignale periodisch wiederholen, wobei die Kopien sich nur um eine Zeitverschiebung unterscheiden. Z. B. könnte das (k+nD)-te Basissignal identisch zum k-ten Basissignal sein bis auf eine Zeitverschiebung um nT. Dabei ist D die Anzahl der „elementaren“ Basissignale, deren Abfolge sich mit Periode T wiederholt. Man kann dann davon sprechen, dass im Zeitraum nT eine Anzahl von nD Symbolen übertragen werden kann.

Es sei angenommen, dass die den Koordinaten zugeordneten Basissignale zueinander orthogonal sind und insgesamt eine orthonormale Basis des Signalvektorraums aufspannen. Ein beliebiges Signal ist dann eine (unendliche) Linearkombination dieser Basissignale. Die Koeffizienten dieser Linearkombination, die den übertragenen Symbolen entsprechen, können nun durch Bilden der Skalarprodukte des Signals mit den Basissignalen zurückgewonnen werden.

Im wichtigen, theorieleitenden Beispiel der bandbeschränkten Übertragungskanäle ist die Symbolrate durch die maximale Frequenz W auf 2 W begrenzt. In einem Zeitintervall endlicher Länge T kann also nur eine endliche Anzahl D von Symbolen übertragen werden. Diese spannen einen Untervektorraum der Dimension D im Signalvektorraum auf. Es sei die nach dem Abtasttheorem maximale Dimension D=2WT angenommen.

Beispiele für Basissignale

Im Folgenden werden einige mathematische, d. h. idealisierte Übertragungskanäle mit ihren Systemen von Basisfunktionen aufgeführt, die die obigen Annahmen für einen Signalvektorraum erfüllen. Diese sind sämtlich bandbeschränkt, wobei neben dem „elementaren“ Basisbandkanal auch Systeme von Basissignalen für Kanäle mit von Null verschiedener minimaler Frequenz angegeben werden können.

Kardinalreihen

Shannon benutzte als einfachstes Signalmodell die Basisbandsignale mit einer höchsten Frequenz W. Nach dem WKS-Abtasttheorem (für Whittaker-Kotelnikow-Shannon, siehe Nyquist-Shannon-Abtasttheorem) können in diesem Kanal gerade 2WT Symbole im Zeitraum T übertragen werden, die Basissignale sind sinc-Funktionen

g_{n}(t)=\operatorname {sinc} (2Wt-n)={\frac {\sin \pi (2Wt-n)}{\pi (2Wt-n)}}

,

n = …, −1, 0, 1, … Diese haben jeweils ihr Zentrum bzw. Maximum bei $t_{n}={\frac {n}{2W}}$ , d. h. die Symbolrate beträgt 2 W. Dieses Orthonormalsystem ist die ideale theoretische Modellierung des frequenzbeschränkten PCM-Verfahrens (Puls-Code-Modulation).

QAM

Das ideale QAM-System (Quadraturamplitudenmodulation) überträgt mit Symbolrate W Daten auf dem Frequenzband [F-W/2, F+W/2]. Dabei muss die mittlere Trägerfrequenz F ein ganzzahliges Vielfaches der Bandbreite W sein. Die Symbole sind hier komplexe Zahlen $A_{n}+iB_{n}$ , d. h. Punkte in der Gaußschen Zahlenebene. Es werden also wieder 2WT reelle Zahlen im Zeitraum T übertragen. Pro komplexem Symbol muss es auch zwei Basisfunktionen geben, diese können zu einer komplexwertigen Funktion zusammengefasst werden:

g_{n}(t)=g_{Q,n}(t)+ig_{I,n}(t)=\operatorname {sinc} (Wt-n)\cdot e^{i2\pi \,Ft}={\frac {\sin \pi (Wt-n)}{\pi (Wt-n)}}(\cos(2\pi \,Ft)+i\sin(2\pi \,Ft))

,

n = …, −1, 0, 1, … Jedes Signal ergibt sich dann als Summe über $A_{n}g_{Q,n}(t)+B_{n}g_{I,n}(t)$ .

OFDM

Das ideale OFDM-System (Orthogonal Frequency Division Multiplexing) überträgt mit Symbolrate W/M einen komplexwertigen Vektor der Dimension M auf dem Frequenzband [F-W/(2M),F+W+W/(2M)]. F muss ein ganzzahliges Vielfaches der Datenrate W/M sein. Es muss also 2M reellwertige Basissignale pro vektorwertigem Symbol geben, die zu M komplexwertigen Funktionen zusammengefasst werden können

g_{j,n}(t)+ig_{M+j,n}(t)=\operatorname {sinc} (Wt/M-n)\cdot e^{-i2\pi \,(F+jW/M)t}

={\frac {\sin \pi (Wt/M-n)}{\pi (Wt/M-n)}}(\cos(2\pi \,(F+jW/M)t)-i\sin(2\pi \,(F+jW/M)t))

,

j = 0, …, M-1, n = …, −1, 0, 1, …

Da die sinc-Funktion technisch nicht zu realisieren ist, muss man andere Lösungen finden. Durch Frequenzfilter wird die Orthogonalität der Basissignale zerstört, es entstehen gegenseitige Störungen innerhalb des Symbols (ICI) und zwischen den Symbolen (ISI). Erhöht man die Taktrate der Signalerzeugung, ohne die Datenrate zu erhöhen, so kann man die gewonnene Freiheit zur Formung eines schon ohne Filterung frequenzbeschränkten Signals nutzen. Eine Variante davon benutzt Wavelet-Paket-Bäume.

Übertragung im rauschgestörten Kanal

Es seien die reellen Basissignale mit einem einzelnen Index durchnummeriert und ein Zeitraum T so fixiert, dass innerhalb dieses Zeitraums D=2WT Basissignale liegen. Gleichmäßiges, auf den Übertragungskanal beschränktes Rauschen kann durch Linearkombinationen $\sum _{n}\varepsilon _{n}g_{n}(t)$ ebendieser Basissignale mit normalverteilten, voneinander unabhängigen zufälligen Koeffizienten $\varepsilon _{n}$ der Varianz $\sigma ^{2}=N$ simuliert werden.

Ein Code der Länge D, d. h. ein Tupel $x_{1},\dots ,x_{D}$ reeller Zahlen, wird als kontinuierliches Signal $f(t)=x_{1}g_{1}(t)+\dots +x_{D}g_{D}(t)$ gesendet. Während der Übertragung wird diesem eine Störung linear überlagert, das empfangene, gestörte Signal ist

{\tilde {f}}(t)=(x_{1}+\varepsilon _{1})g_{1}(t)+\dots +(x_{D}+\varepsilon _{D})g_{D}(t)

.

Geometrie der Signalpunkte

Sei das Signal auf eine durchschnittliche Leistung $P$ beschränkt, wobei Leistung direkt dem Amplitudenquadrat entspreche. Das ist zulässig, da am Ende nur Verhältnisse verschiedener Leistungen verglichen werden, weitere konstante Faktoren sich also kürzen. Da die Basissignale orthonormal sind, hat das kontinuierliche Signal die Quadratsumme seiner Koeffizienten als Leistung, d. h. $\|f\|_{2}^{2}=|x_{1}|^{2}+\dots +|x_{D}|^{2}=DP$ .

Anders gesagt, der Code $(x_{1},\dots ,x_{D})$ ist ein Punkt auf einer D-dimensionalen Sphäre mit Radius $R_{0}:={\sqrt {DP}}$ .

Die Quadratsumme der D voneinander unabhängigen Fehler $(\varepsilon _{1})^{2}+\dots +(\varepsilon _{D})^{2}$ liegt nach dem Gesetz der großen Zahlen dicht bei ihrem Erwartungswert DN. Damit liegt der empfangene Code mit sehr hoher Wahrscheinlichkeit innerhalb einer Kugel vom Radius $r:={\sqrt {DN}}$ mit dem gesendeten Code als Mittelpunkt. Da die Störungen als von Signal unabhängig vorausgesetzt werden, liegt die Quadratsumme des empfangenen Codes mit hoher Wahrscheinlichkeit nahe dem Erwartungswert $R_{1}^{2}:=DP+DN$ , d. h. nahe der Sphäre mit dem Radius $R_{1}$ um den Nullpunkt.

Zufällige Konfiguration

Es sei eine Konfiguration von M=2^DB zufällig ausgewählten Codes mit mittlerer Leistung P fixiert, welche M verschiedenen digitalen Botschaften entsprechen soll, d. h. es werden $DB$ Bit mittels D Basissignalen oder B Bit pro Basissignal kodiert.

Von den kleinen Kugeln mit Radius $r={\sqrt {DN}}$ um die Codes der Konfiguration passen maximal

M={\frac {R_{1}^{D}\operatorname {vol} (K_{D})}{r^{D}\operatorname {vol} (K_{D})}}=\left({\frac {P+N}{N}}\right)^{\frac {D}{2}}

Stück in die große Kugel der empfangbaren Signale, d. h. für die maximale Bitrate gilt (mit D/2=WT)

2WB={\frac {\log _{2}(M)}{T}}\leq W\log _{2}\left(1+{\frac {P}{N}}\right)

.

Abschätzung des Übertragungsfehlers

Für sehr großes D liegen die gesendeten Codes auf einer Kugel mit Radius $R_{0}={\sqrt {DP}}$ und die empfangenen Codes mit hoher Wahrscheinlichkeit in Kugeln mit Radius $r={\sqrt {DN}}$ um diese und auf der Kugel mit Radius $R_{0}={\sqrt {D(P+N)}}$ . Man kann also den empfangenen Code mit allen Codes aus der Konfiguration vergleichen, um den zu bestimmen, der einen Abstand kleiner r hat.

Die Fehlerkugel mit Radius r und mit Mittelpunkt auf der Sphäre der empfangenen Codes überstreicht einen Bereich in der Sphäre der gesendeten Codes, welcher seinerseits innerhalb einer Kugel mit Radius $h={\sqrt {\frac {DNP}{N+P}}}$ liegt. Die Wahrscheinlichkeit, dass ein zufälliger Code außerhalb dieses Bereichs liegt, ist also größer als

1-{\frac {h^{D}\operatorname {vol} (K_{D})}{R_{0}^{D}\operatorname {vol} (K_{D})}}=1-\left({\frac {N}{P+N}}\right)^{\frac {D}{2}}

.

Dass alle M-1 von dem gesendeten Code verschiedenen Codes der Konfiguration außerhalb dieses Bereichs liegen, hat also eine Wahrscheinlichkeit, die größer ist als

\left(1-\left({\frac {N}{P+N}}\right)^{\frac {D}{2}}\right)^{M-1}\geq 1-M\left({\frac {N}{P+N}}\right)^{\frac {D}{2}}

.

Soll eine Fehlerwahrscheinlichkeit e unterschritten werden, d. h. obiger Ausdruck größer als 1-e sein, so erhält man nach Umstellen für die Bitrate

{\frac {\log _{2}(M)}{T}}\leq W\log _{2}\left(1+{\frac {P}{N}}\right)+{\frac {\log _{2}(e)}{T}}

.

$\log _{2}(e)$ im zweiten Summanden ist negativ und im Betrage sehr groß, der Beitrag des zweiten Summanden kann aber beliebig klein gestaltet werden, wenn der Zeitraum T und damit auch die Mächtigkeit M der Konfiguration groß genug sind.

Damit kann, mit wachsender Länge der Signale in der Konfiguration, die Bitrate beliebig nahe an die ideale Bitrate herangeführt werden. Jedoch stellen Verwaltung der Konfiguration und das Suchen des am besten dem empfangenden ähnelnden Signals einer direkten praktischen Anwendung schnell wachsende Anforderungen entgegen.

Literatur

John G. Proakis, Masoud Salehi: Communication Systems Engineering. 2. Auflage. Prentice Hall, Upper Saddle River NJ 2002, ISBN 0-13-095007-6.

Einzelnachweise

Ralph V. L. Hartley: Transmission of Information. Bell System Technical Journal, 1928 (dotrose.com [PDF]).
Claude E. Shannon: The Mathematical Theory of Communication. University of Illinois Press, 1949.
John G. Proakis, Masoud Salehi: Communication Systems Engineering. 2. Auflage. Pearson Education International, ISBN 0-13-095007-6.

Weblinks

Claude Elwood Shannon: Communication in the Presence of Noise (PDF; 301 kB); In: Proc. IRE, Vol. 37, No. 1 (Jan. 1949), Nachdruck in: Proc. IEEE Vol. 86, No. 2, (Feb 1998)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Ralph V. L. Hartley: Transmission of Information. Bell System Technical Journal, 1928 (dotrose.com [PDF]).

[2] Claude E. Shannon: The Mathematical Theory of Communication. University of Illinois Press, 1949.

[3] John G. Proakis, Masoud Salehi: Communication Systems Engineering. 2. Auflage. Pearson Education International, ISBN 0-13-095007-6.