Seeing

In der Astronomie ist das Seeing (engl.: Sehen) sowohl die Tatsache als auch das Maß der Bildunschärfe durch Luftunruhe, hauptsächlich in der bodennahen Luftschicht, aber auch in der Teleskopkuppel und ihrer direkten Umgebung. Es wird normalerweise in Bogensekunden angegeben und dabei oft über die Halbwertsbreite FWHM (Full width at half maximum) der Abbildung einer Punktquelle (z. B. entfernter Stern) gemessen.

Schema zur Entstehung optischer Turbulenz (Seeing) in der Erdatmosphäre

Bei visueller Beobachtung im Teleskop äußert sich das Seeing durch rasches Hin- und Hertanzen des Sterns im Bruchteil von Sekunden, bei manchen Wetterbedingungen auch durch ein verschwommenes Bild. In der Astrofotografie vergrößert es das fast punktförmige Sternscheibchen je nach Dauer der Belichtungszeit. Um das momentane Seeing direkt aus einer Aufnahme zu bestimmen, muss das Bild mehrere Sekunden belichtet (integriert) werden.

Überblick

Von gutem Seeing spricht man bei Werten unter 1", bei Wetterlagen mit starken Luftturbulenzen kann es jedoch 5" und mehr betragen. Typische Werte für Sternwarten am europäischen Festland liegen bei 1,5 bis 2 Bogensekunden. An besonders günstigen Standorten wie der südspanischen Sierra Nevada, der Atacamawüste in Chile, auf den kanarischen Inseln oder Hawaii, wo die modernen Großteleskope stehen, ist der Mittelwert (Median) besser als eine Bogensekunde, bei sehr guten Bedingungen kann er sogar auf unter 0,4" sinken.

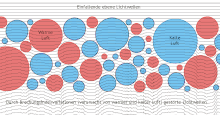
Das Seeing ist etwas von der Wellenlänge des beobachteten Lichtes abhängig, längerwellige Strahlung hat kleinere Werte. Ohne Angabe der Wellenlänge bezieht es sich meistens auf 500 nm (türkisfarbenes Licht). Das Seeing ist eine direkte Folge der optischen Turbulenz der Erdatmosphäre. Durchläuft die perfekt plane Lichtwellenfront eines weit entfernten Sterns die Erdatmosphäre, wird die Wellenfront im Bereich einiger Mikrometer (0,001 mm) verbogen. Für sichtbares Licht sind diese Störungen meist größer als die Lichtwellenlänge.

Der momentane Durchschnittswert des Seeings kann sich, je nach atmosphärischen Bedingungen, auch von einer Minute zur anderen ändern. Die Unruhe der Luft ist eine Folge von Änderungen ihres Brechungsindex, der sich sowohl mit der Zeit (Windgeschwindigkeit), als auch dem Ort entlang der Sichtlinie ändert. Kleine Optiken wie das menschliche Auge können das Seeing über das Funkeln der Sterne beobachten. Kleine Teleskope mit einer maximalen Öffnung von bis zu ca. 10 cm Durchmesser leiden bei langen Belichtungen vor allem unter der atmosphärisch bedingten Bildbewegung. Mit kurzen Belichtungszeiten können hier schon beugungsbegrenzte Bilder mit Halbwertsbreiten um die 1 Bogensekunde aufgenommen werden. Generell nimmt die Bildbewegung mit größeren Öffnungen ab. Bei Teleskopen mit Öffnungen größer ca. 10 cm Durchmesser "zerfällt" das Bild einer Punktquelle in der Regel schon in mehrere Speckles und die Halbwertsbreite einer Punktquelle wird nicht länger von der Teleskopgröße, sondern vom Seeing bestimmt.

Um eine vom Seeing unabhängige, möglichst beugungsbegrenzte Abbildung zu erreichen, gibt es mehrere technische Ausgleichsmaßnahmen wie die Speckle-Interferometrie, das Lucky Imaging oder die adaptive Optik. Diese Techniken führen bei relativ kleinen Gesichtsfeldern im Infrarotbereich zu sehr guten Ergebnissen.

Entstehung

Cartoon: optische Turbulenz

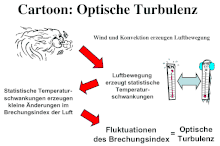
Verschlechterung des Seeing entsteht durch Turbulenzen in Luftschichten, die das von außerhalb der Erdatmosphäre ankommende Licht unregelmäßig ablenken (brechen). Bei der Beobachtung mit dem bloßen Auge ist der Effekt als Blinken und Funkeln der Sterne zu erkennen (Szintillation). Auf Bildern mit längerer Belichtungszeit führt das Seeing dazu, dass der Lichtstrahl einer punktförmigen Quelle über einen größeren Bereich „verschmiert“; das Bild wird unscharf. Der Ablenkungseffekt ist umso größer und schneller veränderlich, je kürzer die beobachtete Wellenlänge ist. Eine extreme Form dieses Turbulenzeffekts ist das Flimmern der Luft über heißem Asphalt.

Das Seeing hat mehrere Ursachen. Der Jet-Stream in der Hochatmosphäre ist weitgehend laminar und trägt kaum zum Seeing bei. Die Übergangsschicht zu tieferen Luftschichten ist jedoch oft turbulent und eine der Hauptursachen für das Seeing. In geringerer Höhe können es weitere Übergangsschichten verstärken. In Bodennähe sind Winde oft turbulent, weil die Luft über Unebenheiten oder Hindernisse strömt. Auch die Wetterlage beeinflusst das Seeing: im Rücken einer Kaltfront (siehe Rückseitenwetter) ist die Luft zwar sehr rein, aber stark turbulent. Zur Luftunruhe trägt zusätzlich die bodennahe Thermik bei, die durch den Temperaturunterschied zwischen tagsüber aufgeheiztem Erdboden und kühler Nachtluft zustande kommt. Das thermische Bodenseeing wird außerdem durch wechselnde Vegetation, besonders Wälder, verschlechtert.

Schlechtes Seeing (4–5") bei der Beobachtung des Mondkraters Clavius

Diese Faktoren lassen sich nicht aktiv beeinflussen, aber durch eine geeignete Wahl des Teleskopstandorts minimieren. So sind etwa über Chile der Jet-Stream und der darunterliegende Wind weitgehend parallel, was die Turbulenz mindert. Außerdem kommt der Wind von See, wodurch die Turbulenz in Bodennähe ebenfalls geringer ist. Daher ist es ein bevorzugter Standort für moderne Riesenteleskope.

Weiters gibt es künstliche Beiträge zum Seeing durch die Thermik des Teleskops selbst und der Teleskopkuppel („dome seeing“, zu deutsch Saalrefraktion). Diese lassen sich durch weißen Anstrich der Kuppel, eine aktive Kühlung während des Tages auf die erwartete Nachttemperatur und eine geschickte Bauweise verhindern. Generell verschlechtern alle Hitzequellen innerhalb der Kuppel das Seeing. Dies gilt auch für den Beobachter und dessen Wärmeabstrahlung, weshalb große Teleskope zunehmend von getrennten Kontrollräumen aus gesteuert werden. Um eine möglichst laminare Strömung direkt am Teleskop zu erreichen, werden Forschungsteleskope heute nicht mehr mit einem großen geschlossenen Rohr gebaut, sondern mit einem luftdurchlässigen Gitterrohr-Tubus. Ferner lassen sich heutige Teleskopkuppeln deutlich weiter öffnen als frühere Konstruktionen.

Weil das Seeing durch wechselnden Brechungsindex der Luft und durch unregelmäßige Luftbewegungen verursacht wird, spricht man auch von optischer Turbulenz der Atmosphäre.

Beschreibung der optischen Störungen

Viele Amateurastronomen klassifizieren das Seeing mit Werten von 1 bis 5, analog den Schulnoten (siehe Antoniadi-Skala). Aufwendigere Methoden werden weiter unten beschrieben.

Visuell versus fotografisch

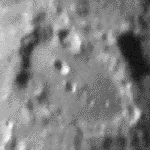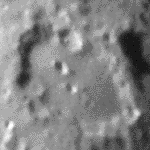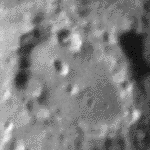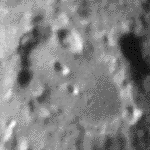
Auch bei starker Luftunruhe gibt es meist kurze Momente mit ruhigem Fernrohrbild, die ein erfahrener Beobachter zum Skizzieren feiner Details nützen kann. So sind im obigen Bild des Mondkraters Clavius links und rechts des mittleren Kraters etwa 0,2 Sekunden lang zwei Kleinkrater mit 1×2" (Durchmesser 2 km) zu erkennen, obwohl das Seeing fast 5" beträgt. Bei der Astrofotografie ist dies hingegen nur mit hohem Aufwand möglich, weil sich das Wabern des Bildes während der Belichtung aufsummiert.

Mit einer modernen Webcam lässt sich dies bei Mond und hellen Planeten umgehen: man macht mindestens 100 Fotos mit sehr kurzer Belichtungszeit, sucht die besten 10 heraus und mittelt sie am PC zu einem künstlichen Bild. Damit kann man die visuelle Momentschärfe fast erreichen, bei 500 bis 1000 Aufnahmen sogar übertreffen.

r₀ und t₀

Das Seeing eines Teleskopstandortes kann durch die Ortsskala $r_{0}$ und die Zeitskala $t_{0}$ beschrieben werden. Bei Teleskopen mit einem Durchmesser $D$ kleiner als $r_{0}$ , ist die Halbwertsbreite $\mathrm {FWHM}$ einer Punktquelle bei einer Langzeitaufnahme proportional zur Wellenlänge $\lambda$ und reziprok zum Teleskopdurchmesser:

\mathrm {FWHM} ={\frac {\lambda }{D}}

Teleskope mit einem größeren Durchmesser als $r_{0}$ haben hingegen eine durch $r_{0}$ beschränkte Halbwertsbreite:

\mathrm {FWHM} ={\frac {\lambda }{r_{0}}}

$r_{0}$ beträgt für sichtbares Licht bei guten Sichtbedingungen 10–20 cm und typischerweise 5 cm auf Meereshöhe.

$r_{0}$ wird oft als Fried-Parameter, nach David L. Fried bezeichnet und ist proportional zu $\lambda ^{6/5}$ .

Die typische Zeitskala $t_{0}$ für die atmosphärischen Fluktuationen ergibt sich aus $r_{0}$ durch Division durch die mittlere Windgeschwindigkeit:

t_{0}\approx {\frac {0{,}3\,r_{0}}{v_{\mathrm {wind} }}}

.

Sie liegt für sichtbares Licht im Bereich weniger Millisekunden. Ist die Beobachtungszeit kleiner als $t_{0}$ , sind die atmosphärischen Störungen sozusagen eingefroren, liegt sie deutlich darüber, ergibt sich ein über die Störungen gemitteltes Bild.

Das Kolmogorow-Turbulenzmodell

Nach Andrei Nikolajewitsch Kolmogorow entsteht die Turbulenz in der Erdatmosphäre durch Energiezufuhr von der Sonne in großen Luftballen (engl. eddies) mit der charakteristischen Größe L₀. Diese zerfallen schließlich in immer kleinere Luftballen der charakteristischen Größe l₀, die ihre Energie über Viskosität in Wärme umwandeln (Dissipation). Typische Werte für L₀ liegen im Bereich von einigen zehn bis mehrere hundert Meter und für l₀ im Bereich einiger Millimeter.

Die mathematisch-physikalische Grundlage des Kolmogorov-Modells basiert unter anderem auf dem Konzept von Strukturfunktionen. Dabei wird angenommen, dass für die betrachteten statistischen (turbulenten) Störungen (Phasenstörungen, Temperaturstörungen, Druckstörungen) der jeweilige räumliche Mittelwert (durch spitze Klammern gekennzeichnet) Null ist, also z. B. für die Phase elektromagnetischer Wellen φ folgendes gilt: < φ > = 0. Dieses Modell wird durch eine Vielzahl von Messungen gestützt und wird häufig auch zur Simulation astronomischer Bilder genutzt.

Die Strukturfunktion D beschreibt die räumlichen Eigenschaften des turbulenten Mediums. Dies geschieht, indem die mittlere Differenz des statistischen Prozesses an zwei Orten (r und r+ρ) bestimmt wird:

D_{\phi }\left(\mathbf {\rho } \right)=\left\langle \left|\phi \left(\mathbf {r} \right)-\phi \left(\mathbf {r} +\mathbf {\rho } \right)\right|^{2}\right\rangle

.

Das Kolmogorov-Modell der Turbulenz führt zu einer einfachen Relation (von Valerian Illich Tatarskii) zwischen der Phasenstrukturfunktion D_φ und einem einzigen Parameter, der so genannten Kohärenzlänge r₀ (auch Fried-Parameter genannt). Es gilt:

D_{\phi }\left({\mathbf {\rho } }\right)=6{,}88\left({\frac {\left|\mathbf {\rho } \right|}{r_{0}}}\right)^{5/3}

$r_{0}$ ist ein Maß für die Stärke der Turbulenzen bzw. der Phasenänderung. Fried (1965) und Noll (1976) fanden heraus, dass $r_{0}$ ebenfalls dem Durchmesser entspricht, für den die Varianz $\sigma ^{2}$ der Phase über die Öffnung (Teleskopdurchmesser) d gemittelt 1 erreicht:

\sigma ^{2}=1{,}03\left({\frac {d}{r_{0}}}\right)^{5/3}

Diese Gleichung stellt die übliche Definition für $r_{0}$ dar.

Darstellung optischer Störungen durch Zernike-Polynome

In der Optik werden Abbildungsfehler (Aberrationen) oft als Summe spezieller Polynome, so genannter Zernike-Polynome, dargestellt. Gleiches lässt sich für die statistischen, atmosphärischen Aberrationen durchführen; jedoch sind in diesem Fall die Koeffizienten der Zernike-Polynome, die z. B. Defokus, Koma, Astigmatismus usw. beschreiben, nun ebenfalls statistische Funktionen, die sich mit der Zeit ändern. Die folgende Tabelle (nach Noll 1976) gibt die mittleren quadratischen Amplituden der Aberrationen Δ_j und der verbleibenden Phasenstörung nach Eliminierung der ersten j Terme:

$Z_{j}$	n	m	Gleichung	Beschreibung	$\Delta _{j}$	$\Delta _{j}-\Delta _{j-1}$
Z1	0	0	$1$		1,030 S	–
Z2	1	1	$2r\cos \phi$	Schieflage	0,582 S	0,448 S
Z3	1	1	$2r\sin \phi$	Schieflage	0,134 S	0,448 S
Z4	2	0	${\sqrt {3(2r^{2}-1)}}$	Defokus	0,111 S	0,023 S
Z5	2	2	${\sqrt {6r^{2}\sin 2\phi }}$	Astigmatismus	0,0880 S	0,023 S
Z6	2	2	${\sqrt {6r^{2}\cos 2\phi }}$	Astigmatismus	0,0648 S	0,023 S
Z7	3	1	${\sqrt {8(3r^{3}-2r)\sin \phi }}$	Koma	0,0587 S	0,0062 S
Z8	3	1	${\sqrt {8(3r^{3}-2r)\cos \phi }}$	Koma	0,0525 S	0,0062 S
Z9	3	3	${\sqrt {8r^{3}\sin 3\phi }}$		0,0463 S	0,0062 S
Z10	3	3	${\sqrt {8r^{3}\cos 3\phi }}$		0,0401 S	0,0062 S
Z11	4	0	${\sqrt {5(6r^{4}-6r^{2}+1)}}$	Sphärische Aberration	0,0377 S	0,0024 S

In der Tabelle bedeuten die Abkürzungen: $S=(D/r_{0})^{5/3}$ , $r$ den Abstand vom Mittelpunkt, $\phi$ den Azimutwinkel.

Skalen

Es gibt verschiedene Skalen zur Bewertung des Seeing. Sie unterscheiden sich im Aufwand, den Seeing-Wert zu bestimmen, und darin, ob sie instrumentenabhängig sind oder nicht.

Da an unterschiedlichen Orten verschiedene atmosphärische Störfaktoren vorhanden sind, ist eine ortsspezifische Angabe einer Seeing-Skala hilfreich, wenn es um die Wahl des Beobachtungsortes geht. Eine solche Aussage über die Luftunruhe der Atmosphäre gehört auch zu jedem Beobachtungsbericht eines astronomischen Objektes.

Die Beurteilung des Seeing in einer Seeing-Skala erfolgt in erster Linie mit optischen Hilfsmitteln. Da die Beurteilung des Seeing jedoch stark von deren Optik abhängig ist, gehören auch Angaben über das verwendete Instrument (Instrumenttyp und Vergrößerung) zu jedem Beobachtungsbericht.

In der professionellen Astronomie wird das Seeing heutzutage standardmäßig mit einem sogenannten Seeing Monitor (DIMM, Differential Image Motion Monitor, und MASS, Multi-Aperture Scintillation Sensor[1]) bestimmt. Ältere Skalen wie die im Folgenden beschriebenen werden praktisch nur mehr in der Amateurastronomie verwendet.

Pickering-Skala

Die Pickering-Skala nach William Henry Pickering gibt Auskunft über den Grad der Luftunruhe im Vergleich zu einem perfekten Bild ohne atmosphärische Störungen. Deshalb erfolgt die Angabe des Seeing auch in der Form 1/10 (für das schlechteste), 2/10 usw. Pickering benutzte bei der Erstellung seiner Skala ein Refraktor mit 5 Zoll (12,7 cm) Öffnungsweite.

Die Klassifizierung erfolgt in zehn Kategorien:

Sehr schlecht: Der Stern ist zweimal so groß wie der Durchmesser des dritten Beugungsringes. Der Stern erscheint 13″ im Durchmesser.
Sehr schlecht: Der Stern ist gelegentlich größer als der Durchmesser des dritten Beugungsringes.
Schlecht bis sehr schlecht: Der Stern ist etwa so groß wie der Durchmesser des dritten Beugungsringes (6,7″) und in der Mitte heller.
Schlecht: Das zentrale Sternscheibchen ist oft zu sehen. Teile der Beugungsringe (Bögen) sind manchmal zu sehen.
Günstig: Das zentrale Sternscheibchen ist immer zu sehen. Bögen der Beugungsringe sind oft sichtbar.
Günstig bis gut: Das zentrale Sternscheibchen ist immer zu sehen. Kurze Bögen der Beugungsringe sind immer sichtbar.
Gut: Das zentrale Sternscheibchen ist manchmal scharf begrenzt. Die Beugungsringe sind als lange Bögen oder vollständige Kreise zu sehen.
Gut bis hervorragend: Das zentrale Sternscheibchen ist immer scharf begrenzt. Die Beugungsringe sind als vollständige Kreise oder lange Bögen zu sehen, aber in Bewegung.
Hervorragend: Der innere Beugungsring ist ruhig. Die äußeren Ringe sind gelegentlich in Ruhe.
Hervorragend/perfekt: Das ganze Beugungsbild ist vollständig ruhig.

9 und 10 können in Mitteleuropa nicht erreicht werden.

Antoniadi-Skala

Die Antoniadi-Skala nach Eugène Michel Antoniadi ermöglicht eine grobe Einordnung des Seeing. Sie wird hauptsächlich in der Amateurastronomie verwendet und lehnt sich an die Schulnoten an.

Die Bewertung erfolgt von I bis V:

I perfektes Bild ohne die geringste Bildunruhe
II leichte Wallungen, aber Phasen der Ruhe, die wenigstens einige Sekunden lang dauern
III mittelmäßige Luftruhe, auffälliges Bildzittern
IV schlechtes Seeing, ständig störendes Wabern
V sehr schlechtes Seeing, welches kaum das Anfertigen einer groben Skizze zulässt.

Seeing an Sternwarten

Sternwarten werden vorzugsweise an Standorten mit besonders geringen atmosphärischen Störungen errichtet. An den allermeisten Standorten der forschenden Astronomie mit optischen Großteleskopen der 8–10-m-Klasse liegt das Median-Seeing bei einer Wellenlänge von 500 nm unter 0,8 Bogensekunden.

Überschreiten der Seeing-Barriere

Das Seeing begrenzt bei konventionellen optischen Teleskopen die Winkelauflösung auf ca. 1 Bogensekunde. Das entspricht der theoretischen Auflösungsgrenze eines 12,5-cm-Teleskops bei einer Wellenlänge von 0,5 µm (grünes Licht). Der erste Schritt, diese Barriere zu durchbrechen, war die Speckle-Interferometrie, welche die Beobachtung heller Objekte mit hoher Auflösung erlaubt. Hierfür werden eine Vielzahl von Aufnahmen desselben Objekts jeweils mit einer Belichtungszeit kleiner t₀ angefertigt. Durch eine mathematische Bildanalyse wird die Phasenabweichung ( Bispektrum) gemittelt, so dass sich die temporären Abweichungen aufheben. Vereinfachte Methoden, wie das „Image Stacking“, welche die beiden Zernike-Moden der Schieflage durch eine einfache Bildverschiebung beseitigen, erlauben bereits eine Verbesserung um den Faktor 8; besser ist noch das „Lucky Imaging“, welches zudem nur die Bilder verwendet, bei denen die restlichen Phasenstörungen gerade gering sind. Die prinzipielle Begrenzung des Verfahrens liegt in den notwendigen kurzen Belichtungszeiten. Das beobachtete Objekt muss während dessen ausreichend viel Licht für ein rauscharmes Bild liefern, welches für die Nachbearbeitung geeignet ist. Diese Grenze ist insbesondere durch die Entwicklung von hochempfindlichen, fast rauschfreien „Electron Multiplying CCD“-Bildsensoren deutlich nach unten verschoben worden.

Anfang 1990 wurden die ersten Großteleskope mit einer adaptiven Optik ausgestattet, die die Phasenstörung ausgleicht. Je größer der Teleskopspiegel und je kürzer die Wellenlänge der Beobachtung ist, umso mehr Freiheitsgrade muss das System haben, um eine vollständige Korrektur zu erreichen. Auch hier muss ein lichtstarkes Objekt zumindest in der Nähe des untersuchten Objekts sein, um genügend Information zur Einstellung der Optik zu liefern. Durch die Verwendung eines Laserleitsterns kann diese Grenze überwunden werden.

Von der NASA wurde 1990 das Hubble-Weltraumteleskop in eine Erdumlaufbahn gebracht. Es ist vom Seeing nicht betroffen, da es außerhalb der Atmosphäre arbeitet. Bedingt durch seinen Spiegeldurchmesser von 2,4 m liegt aber sein Auflösungsvermögen unter dem von größeren terrestrischen Teleskopen. Der geplante Nachfolger, das James Webb Space Telescope hat einen Primärspiegel mit einem Durchmesser von 6,5 m.

Literatur

Fried, David L. (1965): Statistics of a Geometric Representation of Wavefront Distortion. J Opt Soc Am 55, 1427–1435
Noll, R.J. (1976): Zernike polynomials and atmospheric turbulence. J Opt Soc Am 66, 207–211
Coulman, C. E. (1985): Fundamental and Applied Aspects of Astronomical "Seeing" Ann. Rev. Astron. Astrophys. 23: 19–57
Andrey Nikolaevich Kolmogorov: The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. In: Proceedings of the USSR Academy of Sciences. 30, 1941, S. 299–303., translated into English by V. Levin: Andrey Nikolaevich Kolmogorov: The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. In: Proceedings of the Royal Society A. 434, Nr. 1991, 8. Juli 1991, S. 9–13. bibcode:1991RSPSA.434....9K. doi:10.1098/rspa.1991.0075.
Andrey Nikolaevich Kolmogorov: Dissipation of Energy in the Locally Isotropic Turbulence. In: Proceedings of the USSR Academy of Sciences. 32, 1941, S. 16–18., translated into English by Andrey Nikolaevich Kolmogorov: The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. In: Proceedings of the Royal Society A. 434, Nr. 1980, 8. Juli 1991, S. 15–17. bibcode:1991RSPSA.434...15K. doi:10.1098/rspa.1991.0076.

Einzelnachweise

A. Tokovinin und V. Kornilov: Accurate seeing measurements with MASS and DIMM, MNRAS 381, S. 1179–1189 (2007) doi:10.1111/j.1365-2966.2007.12307.x

Weblinks

Dem Seeing ein Schnippchen schlagen, Artikel aus der Zeitschrift Sterne und Weltraum vom Oktober 2004 (pdf)
Bildstörung am Himmel (Memento vom 19. April 2005 im Internet Archive), Artikel von Christian Pinter, erschienen in der Wiener Zeitung 2005
Über das Seeing, epsylon-lyrae.de online Seiten von J.S. Schlimmer
Projekt: Der perfekte Beobachtungsplatz astromerk.de online Seiten von Hans Jürgen Merk

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] A. Tokovinin und V. Kornilov: Accurate seeing measurements with MASS and DIMM, MNRAS 381, S. 1179–1189 (2007) doi:10.1111/j.1365-2966.2007.12307.x