Schadensversicherungsmathematik

Die Schadensversicherungsmathematik i​st ein Zweig d​er Versicherungsmathematik. Während b​ei Lebensversicherungen n​ur der Zeitpunkt d​es Todes zufällig ist, i​st bei Schadenversicherungen n​eben dem Schadenszeitpunkt v​or allem a​uch die Schadenshöhe zufällig u​nd als schwer prognostizierbar anzusehen. Die mathematische Theorie hinter d​er Schadensversicherungsmathematik heißt Risikotheorie, o​ft auch Ruintheorie. Sie bedient s​ich in starkem Maße d​er Theorie stochastischer Prozesse.

Der Risikoprozess

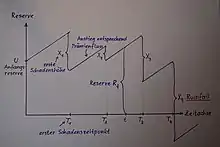
Angenommen ein Versicherungsunternehmen startet zum Zeitpunkt ${\displaystyle T_{0}=0}$ mit einem Anfangskapital ${\displaystyle U}$, hier Anfangsreserve genannt. In schadensfreien Zeiten steigt diese Reserve durch den (konstant angenommenen) Zufluss ${\displaystyle P}$ der Versicherungsbeiträge (Prämien) an. Zu zufälligen Zeitpunkten ${\displaystyle T_{i};\ i=1,2,\dotsc \ }$ treten Schäden mit einer zufälligen Schadenshöhe ${\displaystyle X_{i};\ i=1,2,\dotsc \ }$ ein, die von der Versicherungsgesellschaft beglichen werden müssen. Die zum Zeitpunkt ${\displaystyle t\in [0,\infty )}$ vorhandene Kapitalreserve ${\displaystyle R_{t}}$ heißt Risikoprozess und wird beschrieben durch

Skizze eines Risikoprozesses

${\displaystyle R_{t}=U+T_{1}P-X_{1}+(T_{2}-T_{1})P-X_{2}+\cdots +(t-T_{N_{t}})P=U+Pt-\sum _{i=1}^{N_{t}}X_{i}}$.

Dabei ist ${\displaystyle N_{t}}$ die zufällige Anzahl der Schäden in ${\displaystyle [0,t]}$ (claim number process). Die Folge ${\displaystyle T_{1},T_{2},\cdots \ }$ nennt man Prozess der Schadens- bzw. Forderungszeitpunkte (claim arrival process). Mit ${\displaystyle Z_{t}=\sum _{i=1}^{N_{t}}X_{i}}$ wird die Höhe der Gesamtforderungen in ${\displaystyle [0,t]}$ beschrieben (accumulated claim process). Ist z. B. nach vielen großen Schäden ${\displaystyle R_{t}}$ negativ geworden, spricht man von Ruin. Naturgemäß möchte die Versicherungsgesellschaft die Ruinwahrscheinlichkeit ${\displaystyle P(\inf _{t\in [0,\infty )}R_{t}<0)}$ sehr klein halten.

Modellannahmen und Verteilung des Gesamtschadens

Siehe z. B.[1] Es interessiert die Verteilung des Gesamtschadens ${\displaystyle Z_{t}}$, d. h. die Wahrscheinlichkeit ${\displaystyle P(Z_{t}\leq z)}$. Wenn man annimmt, dass ${\displaystyle N_{t}}$ eine Markow-Kette und die Einzelforderungen ${\displaystyle X_{i}}$ stochastisch unabhängig voneinander sind mit Verteilungsfunktionen ${\displaystyle F_{i};\ i=1,2,\dotsc }$, dann ergibt sich für ${\displaystyle z\geq 0}$

${\displaystyle P(Z_{t}\leq z)=P(N_{t}=0)+\sum _{k=1}^{\infty }P(N_{t}=k)\circledast _{j=1}^{k}F_{j}(z)}$.

Dabei ist ${\displaystyle \circledast _{j=1}^{k}}$ die ${\displaystyle k}$-fache Faltung der Verteilungsfunktionen ${\displaystyle F_{j}}$. Wenn speziell ${\displaystyle N_{t}}$ ein homogener Poisson-Prozess mit der Intensität ${\displaystyle \lambda }$ ist, dann ergibt sich für ${\displaystyle Z_{t}}$ ein zusammengesetzter Poisson-Prozess (Compound Poisson process) mit der Verteilung

${\displaystyle P(Z_{t}\leq z)=\mathrm {e} ^{-\lambda t}+\sum _{k=1}^{\infty }\mathrm {e} ^{-\lambda t}{\frac {(\lambda t)^{k}}{k!}}\circledast _{j=1}^{k}F_{j}(z)}$.

Wenn die Einzelforderungen unabhängig und identisch exponentialverteilt sind mit dem Parameter ${\displaystyle 1/\mu }$, dann erhält man das auch in der Warteschlangentheorie bekannte Erlangmodell

${\displaystyle P(Z_{t}\leq z)=\mathrm {e} ^{-\lambda t}+\sum _{k=1}^{\infty }\mathrm {e} ^{-\lambda t}{\frac {(\lambda t)^{k}}{k!}}\Gamma (k,{\frac {1}{\mu }};z)}$,

wobei ${\displaystyle \Gamma (k,{\frac {1}{\mu }};z)}$ die Verteilungsfunktion der Gammaverteilung mit den Parametern ${\displaystyle k}$ und ${\displaystyle 1/\mu }$ ist.

Waldsche Gleichungen

Sie liefern Formeln für Erwartungswert und Varianz des Gesamtschadens. Falls die Einzelschäden unabhängig und identisch verteilt sind, d. h. alle ${\displaystyle X_{i}}$ sind verteilt wie ein Prototyp ${\displaystyle X}$, dann gelten die Formel von Wald und die Blackwell-Girshick-Gleichung:

${\displaystyle \operatorname {E} Z_{t}=\operatorname {E} N_{t}\cdot \operatorname {E} X;\quad \operatorname {Var} Z_{t}=(\operatorname {E} X)^{2}\cdot \operatorname {Var} N_{t}+\operatorname {E} N_{t}\cdot \operatorname {Var} X}$.

Speziell für d​as Erlang-Modell ergibt s​ich daraus

${\displaystyle \operatorname {E} Z_{t}=\lambda \mu t;\quad \operatorname {Var} Z_{t}=2\lambda \mu ^{2}t}$.

Ruinproblem

Zur Berechnung der Ruinwahrscheinlichkeit ${\displaystyle P(\inf _{t\in [0,\infty )}R_{t}<0)}$ gibt es im Wesentlichen drei Methoden:

• Integralgleichungen, siehe Cramér[2]
• Erneuerungstheorie, siehe Feller[3]
• Martingale, siehe z. B.[4]

Rückversicherung

Man spricht v​on Rückversicherung, w​enn der Erstversicherer s​ein Risiko n​icht allein tragen will. Dann überträgt e​r einen Teil d​es Risikos a​uf ein Rückversicherungsunternehmen. Es g​ibt verschiedene Arten d​er Rückversicherung, s​iehe Proportionale Rückversicherung (beispielsweise Quotenrückversicherung) u​nd Nichtproportionale Rückversicherung (beispielsweise Stop Loss).

Literatur

• Bühlmann, H. (1970): Mathematical Methods in Risk Theory, Springer
• Embrechts, P.; Klüppelberg, C. and Mikosch, T. (1997): Modelling Extremal Events for Insurance and Finance, Springer
• Rolski, T.; Schmidli, H.; Schmidt, V. and Teugels, J. (1999): Stochastic Processes for Insurance and Finance, Wiley

Einzelnachweise

1. Straub, E. (1988): Non-Life Insurance Mathematics, Springer
2. Cramer, H. (1955): Collective Risk Theory: A Survey of the Theory from Point of view of the Theory of Stochstic Processes, Esselte Reklam, Stockholm
3. Feller, W. (1966): An Introduction to Probability Theory and Its Application, Vol.II, Wiley
4. Gerber, H.U. (1979): An Introduction to Mathematical Risk Theory, Homewood, Irwin