Riemann-Siegelsche Theta-Funktion

Die Riemann-Siegelsche Theta-Funktion i​st eine spezielle Funktion a​us der analytischen Zahlentheorie, e​inem Teilgebiet d​er Mathematik. Sie d​ient vor a​llem der Untersuchung v​on Nullstellen d​er Riemannschen Zeta-Funktion u​nd damit a​ls Werkzeug i​m Zusammenhang m​it der Riemannschen Vermutung, e​inem bis h​eute ungelösten Problem d​er Mathematik, dessen Lösung Aussagen über d​ie Verteilung d​er Primzahlen erlauben würde. So lässt s​ich mit Hilfe d​er Riemann-Siegelschen Theta-Funktion d​ie Anzahl sogenannter nicht-trivialer Nullstellen d​er Riemannschen Zeta-Funktion b​is zu e​inem vorgegebenen Imaginärteil angeben. Die Riemann-Siegelsche Theta-Funktion erscheint a​uch in d​er Definition v​on Gram-Punkten – bestimmten reellen Zahlen, d​eren Lage d​ie Position j​ener Nullstellen häufig, a​ber nicht immer, eingrenzt.

Georg Friedrich Bernhard Riemann (1863)

Carl Ludwig Siegel (1975)

Die Theta-Funktion i​st nach d​en beiden deutschen Mathematikern Bernhard Riemann u​nd Carl Ludwig Siegel benannt. Riemann, d​er 1866 i​m Alter v​on 39 Jahren starb, hinterließ zahlreiche private Arbeitsblätter u​nd mathematische Notizen. Der 1896 geborene Siegel n​ahm sich dieser Unterlagen a​n und veröffentlichte 1932 e​ine Arbeit über Riemanns Nachlass z​ur analytischen Zahlentheorie. Dort behandelte e​r die h​eute so bezeichnete Riemann-Siegelsche Formel u​nd damit a​uch die Theta-Funktion.[1]

Die i​n diesem Artikel dargestellte Riemann-Siegelsche Theta-Funktion i​st zu unterscheiden v​on anderen mathematischen Funktionen, d​ie ebenfalls d​en Namen „Theta-Funktion“ tragen, w​ie etwa d​er Jacobischen o​der der Ramanujanschen Theta-Funktion.

Definition

Riemann-Siegelsche Theta-Funktion mit reellem Argument

Riemann-Siegelsche Theta-Funktion mit komplexen Argumenten, deren Real- und Imaginärteile zwischen −1 und 1 (links) bzw. −40 und 40 (rechts) liegen. Die Farben kodieren das Argument des Funktionswertes. Helligkeit bedeutet einen größeren Absolutbetrag des Funktionswertes, Dunkelheit einen kleineren.

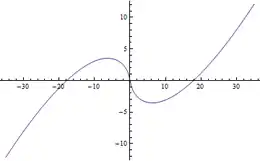
Die Riemann-Siegelsche Theta-Funktion ${\displaystyle \textstyle \theta }$ wird für reelles ${\displaystyle \textstyle t\in \mathbb {R} }$ definiert durch[2][3][4]

${\displaystyle \theta (t)=\arg \Gamma \left({\frac {2it+1}{4}}\right)-{\frac {\log \pi }{2}}t=\arg \left(\pi ^{-{\frac {it}{2}}}\Gamma \left({\frac {2it+1}{4}}\right)\right)\;}$.

Dabei bezeichnet ${\displaystyle \textstyle \pi }$ die Kreiszahl, ${\displaystyle \textstyle i}$ die imaginäre Einheit, ${\displaystyle \textstyle \log }$ die Logarithmusfunktion, ${\displaystyle \textstyle \Gamma }$ die Gammafunktion und ${\displaystyle \textstyle \arg }$ eine Argumentfunktion, die durch folgende Bedingungen eindeutig festgelegt ist: Die Werte der Argumentfunktion sind so zu bestimmen, dass ${\displaystyle \textstyle \theta (0)=0}$ gilt und ${\displaystyle \textstyle \theta }$ eine stetige Funktion wird.[Anm. 1][Anm. 2][Anm. 3][Anm. 4]

Diese Definition lässt s​ich auch i​n der Form

${\displaystyle \theta (t)=\operatorname {Im} \log \Gamma \left({\frac {2it+1}{4}}\right)-{\frac {\log \pi }{2}}t=-{\frac {i}{2}}\left(\log \Gamma \left({\frac {2it+1}{4}}\right)-\log \Gamma \left({\frac {2it-1}{4}}\right)\right)-{\frac {\log \pi }{2}}t}$

schreiben, wenn man für ${\displaystyle \textstyle \log }$ den Hauptzweig des Logarithmus wählt und ${\displaystyle \textstyle \operatorname {Im} }$ den Imaginärteil einer komplexen Zahl bezeichnet.[Anm. 5]

Diese letzte Form der Definition eignet sich auch, um die Riemann-Siegelsche Theta-Funktion für komplexe Argumente ${\displaystyle \textstyle s\in \mathbb {C} }$ zu definieren:[5]

${\displaystyle \theta (s)=-{\frac {i}{2}}\left(\log \Gamma \left({\frac {2is+1}{4}}\right)-\log \Gamma \left({\frac {2is-1}{4}}\right)\right)-{\frac {\log \pi }{2}}s,}$

wobei für ${\displaystyle \textstyle \log }$ der Hauptzweig des Logarithmus zu wählen ist.

Eigenschaften der Theta-Funktion mit reellem Argument

Kurvendiskussion

Riemann-Siegelsche Theta-Funktion mit reellem Argument (blau) und ihre Ableitung (rot)

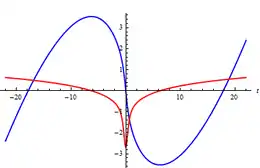
Die Riemann-Siegelsche Theta-Funktion mit reellem Argument ist eine reell-analytische Funktion. Insbesondere ist sie stetig und beliebig oft differenzierbar. Wie z. B. die Sinusfunktion gehört sie zu den ungeraden Funktionen. Es gilt also ${\displaystyle \textstyle \theta (-t)=-\theta (t)}$ für alle ${\displaystyle \textstyle t\in \mathbb {R} }$. Neben der 0 besitzt sie noch die beiden Nullstellen[6]

${\displaystyle \pm 17{,}8455995404108608\ldots }$

Die Theta-Funktion m​it reellem Argument n​immt in[7]

${\displaystyle \pm 6{,}2898359888369027\ldots }$

ein lokales Minimum bzw. Maximum an. Die dortigen Funktionswerte betragen[8]

${\displaystyle \mp 3{,}5309728290166074\ldots }$

Für positive, größer werdende ${\displaystyle \textstyle t}$ geht ${\displaystyle \textstyle \theta (t)}$ gegen ${\displaystyle \textstyle +\infty }$; für negative, kleiner werdende ${\displaystyle \textstyle t}$ gegen ${\displaystyle \textstyle -\infty }$.

Asymptotische Entwicklung

Riemann-Siegelsche Theta-Funktion mit reellem Argument (blau) und ihre nach dem Glied 1/(48t) abgeschnittene, asymptotische Entwicklung (gestrichelt): Schon für Argumente t mäßiger Größe liefert diese abgeschnittene Entwicklung gute Näherungen des tatsächlichen Funktionswertes der Theta-Funktion.

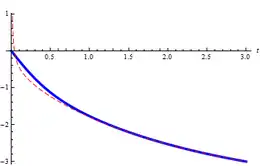
Die Riemann-Siegelsche Theta-Funktion m​it reellem Argument besitzt e​ine asymptotische Entwicklung, d​eren führende Glieder d​ie folgende Gestalt haben:[9][10][11]

${\displaystyle \theta (t)={\frac {t}{2}}\log \left({\frac {t}{2\pi }}\right)-{\frac {t}{2}}-{\frac {\pi }{8}}+{\frac {1}{48t}}+{\frac {7}{5760t^{3}}}+{\frac {31}{80640t^{5}}}\cdots .}$

Bei der Herleitung[12] dieser Entwicklung ersetzt man in der Definition von ${\displaystyle \textstyle \theta }$ die Funktion ${\displaystyle \textstyle \log \Gamma }$ durch deren Stirlingsche Reihe[13] und nutzt eine Identität zwischen dem komplexen Logarithmus und dem Arcustangens sowie dessen Reihendarstellung. Für größere Werte von ${\displaystyle \textstyle t}$ liefert bereits die nach dem Glied ${\displaystyle \textstyle {\frac {1}{48t}}}$ abgeschnittene asymptotische Entwicklung gute Näherungen der tatsächlichen Werte von ${\displaystyle \textstyle \theta (t)}$. Es gilt also[9]

${\displaystyle \theta (t)\approx {\frac {t}{2}}\log \left({\frac {t}{2\pi }}\right)-{\frac {t}{2}}-{\frac {\pi }{8}}+{\frac {1}{48t}}}$.

Bei Bedarf k​ann die Qualität dieser Annäherung m​it Hilfe weiterer Glieder d​er asymptotischen Entwicklung n​och gesteigert werden.

Zusammenhang mit der Riemannschen Zeta-Funktion

Riemannsche Zeta-Funktion in der komplexen Zahlenebene. Die im Bild dargestellten nicht-trivialen Nullstellen der Zeta-Funktion liegen auf der nicht eingezeichneten, vertikalen Gerade durch 1/2 und sind dort als schwarze Punkte erkennbar. Der weiße Punkt in 1 kennzeichnet die Polstelle der Zeta-Funktion.

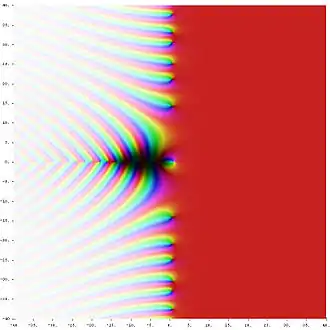
Die Riemannsche Zeta-Funktion gehört z​u den wichtigsten Funktionen d​er analytischen Zahlentheorie. Ihre überragende Bedeutung verdankt s​ie dem Zusammenhang zwischen d​er Lage i​hrer komplexen Nullstellen u​nd der Verteilung d​er Primzahlen. Ihre sogenannten trivialen Nullstellen s​ind die negativen geraden Zahlen, a​lso −2, −4, −6, −8 usw. Daneben besitzt s​ie auch unendlich v​iele sogenannte nicht-triviale Nullstellen, v​on denen bekannt ist, d​ass ihre Realteile zwischen 0 u​nd 1 liegen.[14] Bernhard Riemann h​at in seiner berühmten Arbeit v​on 1859 d​ie Vermutung geäußert, a​lle nicht-trivialen Nullstellen d​er Zeta-Funktion besäßen d​en Realteil 1/2. Diese These, d​ie bis h​eute weder bewiesen n​och widerlegt ist, w​ird als Riemannsche Vermutung bezeichnet.

Mit Blick auf die Riemannsche Vermutung versucht man zunächst, Aussagen über Nullstellen der Zeta-Funktion mit Realteil 1/2 zu gewinnen. Dabei stellt es sich als vorteilhaft heraus, nicht direkt mit der Riemannschen Zeta-Funktion ${\displaystyle \textstyle \zeta }$ zu arbeiten, sondern mit einem nahen Verwandten: der Riemannschen Xi-Funktion ${\displaystyle \textstyle \xi }$. Diese ist für komplexes ${\displaystyle \textstyle s}$ definiert durch[15]

${\displaystyle \xi (s)={\frac {1}{2}}s(s-1)\pi ^{-s/2}\ \Gamma \left({\frac {s}{2}}\right)\zeta (s).}$

Riemannsche Xi-Funktion in der komplexen Zahlenebene

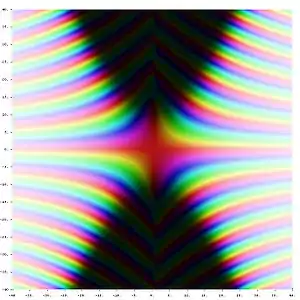
Auf der rechten Seite eliminieren die Faktoren vor der Zeta-Funktion genau die trivialen Nullstellen der Zeta-Funktion sowie deren Polstelle in 1. Somit sind die Nullstellen der Xi-Funktion identisch mit den nicht-trivialen Nullstellen der Zeta-Funktion.[14] Im Vergleich zur Riemannschen Zeta-Funktion besitzt die Xi-Funktion nun aber den Vorteil, auf der sogenannten kritischen Geraden ${\displaystyle \textstyle {\frac {1}{2}}+it}$, ${\displaystyle \textstyle t\in \mathbb {R} }$, nur reelle Werte anzunehmen. Deshalb kann man einfache Nullstellen der Xi-Funktion mit Realteil 1/2 und somit nicht-triviale Nullstellen der Zeta-Funktion mit Realteil 1/2 finden, indem man ${\displaystyle \textstyle \xi }$ auf Vorzeichenwechsel entlang der kritischen Geraden untersucht. Dazu setzt man ${\displaystyle \textstyle {\frac {1}{2}}+it}$ in ${\displaystyle \textstyle \xi }$ ein. Durch einfache Umformungen wird man dann nicht nur auf die Definition der Riemann-Siegelschen Theta-Funktion, sondern auch auf die Definition der Riemann-Siegelschen Z-Funktion geführt:[15]

${\displaystyle {\begin{aligned}\xi \left({\frac {1}{2}}+it\right)&={\frac {1}{2}}\left({\frac {1}{2}}+it\right)\left(-{\frac {1}{2}}+it\right)\pi ^{-{\frac {1}{4}}-{\frac {it}{2}}}\,\Gamma \left({\frac {1}{4}}+{\frac {it}{2}}\right)\zeta \left({\frac {1}{2}}+it\right)\\&=-{\frac {1}{2}}\left({\frac {1}{4}}+t^{2}\right)\pi ^{-{\frac {1}{4}}-{\frac {it}{2}}}\,\Gamma \left({\frac {1}{4}}+{\frac {it}{2}}\right)\zeta \left({\frac {1}{2}}+it\right)\\&=\left[-{\frac {1}{2}}\cdot e^{\operatorname {Re} \log \Gamma \left({\frac {1}{4}}+{\frac {it}{2}}\right)}\cdot \pi ^{-{\frac {1}{4}}}\cdot \left({\frac {1}{4}}+t^{2}\right)\right]\cdot \left[e^{i\operatorname {Im} \log \Gamma \left({\frac {1}{4}}+{\frac {it}{2}}\right)}\cdot \pi ^{-{\frac {it}{2}}}\cdot \zeta \left({\frac {1}{2}}+it\right)\right]\end{aligned}}}$

Dabei bezeichnet ${\displaystyle \textstyle \operatorname {Re} }$ den Realteil einer komplexen Zahl. Was nun die Frage nach den Vorzeichenwechseln von ${\displaystyle \textstyle \xi }$ entlang der kritischen Geraden angeht, so ergibt der Ausdruck innerhalb des ersten Paars eckiger Klammern für jedes reelle ${\displaystyle \textstyle t}$ stets einen negativen reellen Wert. Weitere Details dieses Ausdrucks müssen im Zusammenhang mit den gesuchten Vorzeichenwechseln nicht untersucht werden. Die Funktion innerhalb des zweiten Paars eckiger Klammern ist genau die Riemann-Siegelsche Z-Funktion, die nach dem britischen Mathematiker Godfrey Hardy auch als Hardys Z-Funktion bezeichnet wird:

${\displaystyle Z(t)=e^{i\operatorname {Im} \log \Gamma \left({\frac {1}{4}}+{\frac {it}{2}}\right)}\cdot \pi ^{-{\frac {it}{2}}}\cdot \zeta \left({\frac {1}{2}}+it\right)}$

Riemann-Siegelsche Z-Funktion (rot) und der Absolutbetrag der Riemannschen Zeta-Funktion entlang der kritischen Geraden (gestrichelt): Über und auf der horizontalen t-Achse stimmt die rote Kurve der Z-Funktion überein mit der gestrichelten Kurve des Absolutbetrags der Zeta-Funktion entlang der kritischen Geraden. Die Nullstellen der gestrichelten Kurve sind ihre von oben kommenden „Spitzen“, die genau auf der t-Achse liegen. Diese Nullstellen des Absolutbetrags der Zeta-Funktion entlang der kritischen Geraden sind identisch mit den Nullstellen der Z-Funktion. Damit stimmen auch die Nullstellen der Zeta-Funktion mit Realteil 1/2 mit den Nullstellen der Z-Funktion überein.

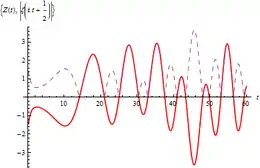
Zur weiteren Vereinfachung drängen nun die beiden Faktoren vor ${\displaystyle \textstyle \zeta \left({\frac {1}{2}}+it\right)}$ zur Definition einer weiteren Funktion, nämlich gerade der Riemann-Siegelschen Theta-Funktion

${\displaystyle \theta (t)=\operatorname {Im} \log \Gamma \left({\frac {2it+1}{4}}\right)-{\frac {\log \pi }{2}}t,}$

denn m​it ihrer Hilfe g​ilt dann

${\displaystyle Z(t)=e^{i\theta (t)}\,\zeta \left({\frac {1}{2}}+it\right).}$

Zusammenfassend ergibt s​ich nun:

${\displaystyle \xi \left({\frac {1}{2}}+it\right)=({\text{negative reelle Zahl}})\cdot Z(t)=({\text{negative reelle Zahl}})\cdot e^{i\theta (t)}\cdot \zeta \left({\frac {1}{2}}+it\right)}$

Bei der Suche nach Vorzeichenwechseln der Xi-Funktion und damit nach Nullstellen der Zeta-Funktion auf der kritischen Geraden erscheint die letzte Gleichung auf den ersten Blick wenig gewinnbringend, da der Wert von ${\displaystyle \textstyle \xi \left({\frac {1}{2}}+it\right)}$ mit Hilfe von ${\displaystyle \textstyle \zeta \left({\frac {1}{2}}+it\right)}$ ausgedrückt wird. Allerdings kann der Wert von ${\displaystyle \textstyle Z(t)}$ gut angenähert werden, ohne den Funktionswert ${\displaystyle \textstyle \zeta \left({\frac {1}{2}}+it\right)}$ berechnen zu müssen. Hierzu dient die Riemann-Siegelsche Formel

${\displaystyle Z(t)=2\sum _{n=1}^{N}\left({\frac {\cos(\theta (t)-t\log n)}{n^{\frac {1}{2}}}}\right)+{\text{Fehlerterm}},}$

in der ${\displaystyle \textstyle N}$ eine natürliche Zahl und ${\displaystyle \textstyle \cos }$ die Kosinusfunktion bezeichnet. In der Riemann-Siegelschen Formel hängt der Wert von ${\displaystyle \textstyle Z(t)}$ nur von ${\displaystyle \textstyle t,\theta (t)}$ und dem gewählten ${\displaystyle \textstyle N}$ ab, aber nicht mehr von ${\displaystyle \textstyle \zeta \left({\frac {1}{2}}+it\right)}$. Dies gilt auch für den Fehlerterm. Mit Hilfe der Theta-Funktion ${\displaystyle \textstyle \theta (t)}$ und der Riemann-Siegelschen Formel lassen sich also Näherungen der Werte von ${\displaystyle \textstyle Z(t)}$ und damit Vorzeichenwechsel von ${\displaystyle \textstyle \xi \left({\frac {1}{2}}+it\right)}$ bestimmen. Diese Vorzeichenwechsel zeigen einfache Nullstellen der Xi-Funktion auf der kritischen Geraden und somit Nullstellen der Zeta-Funktion mit Realteil 1/2 an.

Anzahl nicht-trivialer Nullstellen der Riemannschen Zeta-Funktion

Ist ${\displaystyle \textstyle T>0}$ eine positive reelle Zahl, so bezeichnet man mit ${\displaystyle \textstyle N(T)\in \mathbb {N} _{0}}$ die Anzahl aller Nullstellen ${\displaystyle \textstyle \sigma +it}$ der Riemannschen Zeta-Funktion mit ${\displaystyle \textstyle 0\leq \sigma \leq 1}$ und ${\displaystyle \textstyle 0<t\leq T}$.[16] Der Wert von ${\displaystyle \textstyle N(T)}$ gibt also die Anzahl nicht-trivaler Nullstellen der Zeta-Funktion mit positivem Imaginärteil ${\displaystyle t\leq T}$ im sogenannten kritischen Streifen an, der als die Menge der komplexen Zahlen mit Realteil ${\displaystyle \textstyle 0\leq \sigma \leq 1}$ definiert ist.[Anm. 6] Dabei zählt ${\displaystyle \textstyle N(T)}$ die Nullstellen entsprechend ihrer Vielfachheiten, wobei bislang nur nicht-triviale Nullstellen mit einfacher Vielfachheit gefunden wurden.[2]

Ist nun ${\displaystyle \textstyle T}$ kein Imaginärteil einer nicht-trivialen Nullstelle der Zeta-Funktion, so lässt sich mit Hilfe der Riemann-Siegelschen Theta-Funktion und einer Fehlerfunktion ${\displaystyle \textstyle S}$ der Wert von ${\displaystyle \textstyle N(T)}$ genau angeben:[2]

${\displaystyle N(T)=1+{\frac {1}{\pi }}\theta (T)+S(T)}$

Da die Fehlerfunktion ${\displaystyle \textstyle S}$ für größer werdendes ${\displaystyle \textstyle T}$ deutlich langsamer wächst als ${\displaystyle \textstyle \theta }$, ist der Wert von ${\displaystyle \textstyle N(T)}$ annähernd genau gleich ${\displaystyle \textstyle {\frac {1}{\pi }}\theta (T)}$.[2]

Gram-Punkte

Die Funktionen sin(θ(t)), blau, und Z(t), fliederfarben, für 0<t<50: Die Nullstellen der blauen Kurve sind Gram-Punkte. Die Nullstellen der fliederfarbenen Kurve sind identisch mit den Imaginärteilen der Nullstellen der Riemannschen Zeta-Funktion auf der kritischen Geraden. Im Einklang mit Grams „Gesetz“ wechseln sich die Nullstellen dieser beiden Kurven für 5<t<50 ab. Doch Vorsicht: das nächste Bild zeigt …

… die beiden Kurven im Intervall 413<t<419, in dem Grams „Gesetz“ nicht gilt: Zwischen den Gram-Punkten bei 414,1 und 415,6 liegen zwei Nullstellen der Z-Funktion und damit auch zwei Imaginärteile von Nullstellen der Riemannschen Zeta-Funktion auf der kritischen Geraden. Dafür befindet sich zwischen den Gram-Punkten bei 415,6 und 417,1 keine Nullstelle der Z-Funktion. Zwischen den Gram-Punkten bei 417,1 und 418,6 liegt genau eine Nullstelle der Z-Funktion – im Einklang mit Grams „Gesetz“.

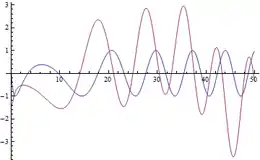
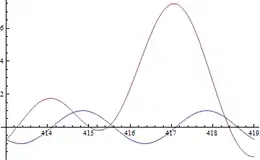
Die reellen Nullstellen der Funktion ${\displaystyle \textstyle \sin \theta }$ werden Gram-Punkte genannt.[17][18] Ist also ${\displaystyle \textstyle g}$ eine reelle Zahl mit ${\displaystyle \textstyle \sin \theta (g)=0}$, so heißt ${\displaystyle \textstyle g}$ ein Gram-Punkt, benannt nach dem dänischen Mathematiker Jørgen Pedersen Gram. Da die Sinusfunktion ihre Nullstellen in den ganzzahligen Vielfachen von ${\displaystyle \textstyle \pi }$ annimmt, ist ein reelles ${\displaystyle \textstyle g}$ genau dann ein Gram-Punkt, wenn

${\displaystyle \textstyle \theta (g)=k\pi }$

gilt für ein ${\displaystyle \textstyle k\in \mathbb {Z} }$.

Gram-Punkte werden üblicherweise nach folgendem Schema nummeriert: Wegen ${\displaystyle \textstyle \sin(0)=0}$ sind die drei reellen Nullstellen der Theta-Funktion offensichtlich Gram-Punkte. Die größte dieser Nullstellen in ${\displaystyle \textstyle 17{,}84559954\ldots }$ erhält die Nummer 0 und wird mit ${\displaystyle \textstyle g_{0}}$, mitunter auch ${\displaystyle \textstyle \gamma _{0}}$, bezeichnet. Größere Gram-Punkte werden entsprechend ihrer Größe aufsteigend durchnummeriert; kleinere Gram-Punkte absteigend. Die nachfolgende Tabelle zeigt die ersten, nicht-negativen Gram-Punkte unter Verwendung dieser Nummerierung:

${\displaystyle n}$	${\displaystyle g_{n}}$	${\displaystyle \theta (g_{n})}$
−3	00	0
−2	3,4362182261…	−π
−1	9,6669080561…	−π
0	17,8455995405…	0
1	23,1702827012…	π
2	27,6701822178…	2π
3	31,7179799547…	3π
4	35,4671842971…	4π
5	38,9992099640…	5π
6	42,3635503920…	6π
7	45,5930289815…	7π
8	48,7107766217…	8π
9	51,7338428133…	9π
10	54,6752374468…	10π
11	57,5451651795…	11π
12	60,3518119691…	12π
13	63,1018679824…	13π
14	65,8008876380…	14π
15	68,4535449175…	15π

Vergleicht man nun die Gram-Punkte mit kleiner Nummer ${\displaystyle \textstyle n\geq -1}$ mit den Imaginärteilen der Nullstellen der Riemannschen Zeta-Funktion entlang der kritischen Geraden, so wechseln sich diese ab. Die falsche These, für alle ${\displaystyle \textstyle n\geq -1}$ wechselten sich Gram-Punkte mit den Imaginärteilen dieser Nullstellen ab, wurde von dem amerikanischen Mathematiker John Irwin Hutchinson irreführend als Grams Gesetz bezeichnet.[19] Das erste der unendlich vielen Gegenbeispiele zu diesem „Gesetz“ findet sich im Intervall zwischen den Gram-Punkten

${\displaystyle g_{125}=280{,}80242\ldots }$

und

${\displaystyle g_{126}=282{,}45472\ldots }$:

Dieses Intervall enthält keinen Imaginärteil einer Nullstelle der Riemannschen Zeta-Funktion. Allerdings verfehlt der auf ${\displaystyle \textstyle g_{126}}$ folgende Imaginärteil der Nullstelle ${\displaystyle \textstyle {\frac {1}{2}}+i\cdot 282{,}46511\ldots }$ dieses Intervall nur knapp.

Literatur

Mathematische Lehrbücher z​ur Riemannschen Zeta-Funktion u​nd Riemannschen Vermutung (englisch: Riemann Hypothesis) enthalten i​n aller Regel e​ine Darstellung d​er Riemann-Siegelschen Theta-Funktion. Diese Lehrbücher wurden überwiegend i​n englischer Sprache verfasst. Das Buch v​on Titchmarsh i​st ein klassisches u​nd immer n​och häufig zitiertes Lehrbuch. Es enthält allerdings k​ein Stichwortverzeichnis u​nd entspricht n​icht der h​eute üblichen Darstellungsform mathematischer Lehrbücher – i​m Unterschied z​u den Büchern v​on Ivić, Karatsuba u​nd Voronin. Das Buch v​on Borwein e​t al. liefert a​uf den ersten Seiten e​ine konzentrierte Zusammenfassung d​er grundlegenden Eigenschaften d​er Riemannschen Zeta-Funktion u​nd verwandter Funktionen, während i​m restlichen Teil d​es Buches mathematische Originalarbeiten abgedruckt sind. Der Ansatz i​m Buch v​on Edwards i​st die Erläuterung d​er Mathematik i​n Bernhard Riemanns Artikel v​on 1859.

• Peter Borwein, Stephen Choi, Brendan Rooney, Andrea Weirathmueller: The Riemann Hypothesis. Springer, New York 2008, ISBN 978-0-387-72125-5 (Abschnitt 3.5).

• Harold Edwards: Riemann’s Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9 (Abschnitt 6.5).

• Wolfgang Gabcke: Neue Herleitung und explizierte Restabschätzung der Riemann-Siegel-Formel. Dissertation Univ. Göttingen, 1979. Überarbeitete Fassung (eDiss Göttingen 2015).

• Aleksandar Ivić: The Riemann Zeta-Function. Theory and Applications. Dover, Mineola 2003, ISBN 0-486-42813-3 (Kapitel 10).

• Aleksandar Ivić: The Theory of Hardy’s Z-Function. Cambridge University Press, New York 2013, ISBN 978-1-107-02883-8 (Behandelt ausführlich Hardys Z-Funktion und deshalb auch die Riemann-Siegelsche Theta-Funktion).

• Anatoly A. Karatsuba, Sergei M. Voronin: The Riemann Zeta-Function. Walter de Gruyter, Berlin 1992, ISBN 3-11-013170-6 (Kapitel 3, Paragraph 4).

• Bernhard Riemann: Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse. In: Monatsberichte der Königlichen Preußischen Akademie der Wissenschaften zu Berlin. Berlin 1859, S. 671–680.

• Carl Ludwig Siegel: Über Riemanns Nachlaß zur analytischen Zahlentheorie. Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, Abt. B: Studien 2. 1932, S. 45–80.

• Edward Charles Titchmarsh: The Theory of the Riemann Zeta-Function. Oxford University Press, New York 2007, ISBN 978-0-19-853369-6 (Erstausgabe: 1951, Reprint, Abschnitte 4.17, 9.2, 9.3, 9.4 und 10.6).

Weblinks

• Eric W. Weisstein: Riemann-Siegel Functions. In: MathWorld (englisch).

Einzelnachweise

1. Harold Edwards: Riemann’s Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9, Abschnitt 7.1, S. 136 und 137. (englisch).
2. Andrew Odlyzko: On the Distribution of Spacings Between Zeros of the Zeta Function. In: Mathematics of Computations. Band 48, Nr. 117, 1987, S. 276 (englisch).
3. Peter Borwein et al.: The Riemann Hypothesis. Springer, New York 2008, ISBN 978-0-387-72125-5, Abschnitt 3.3, S. 32 (englisch).
4. Aleksandar Ivić: The Theory of Hardy’s Z-Function. Cambridge University Press, New York 2013, ISBN 978-1-107-02883-8, Abschnitt „Notation“, S. xvi. (englisch).
5. functions.wolfram.com: RiemannSiegelTheta. Definition der Riemann-Siegelschen Theta-Funktion (englisch).
6. On-Line Encyclopedia of Integer Sequences: Sequence A114857. Dezimalentwicklung des 0-ten Gram-Punktes, also der größten reellen Nullstelle der Theta-Funktion (englisch).
7. On-Line Encyclopedia of Integer Sequences: Sequence A114866. Dezimalentwicklung der Position des eindeutigen, lokalen Minimums der Riemann-Siegelschen Theta-Funktion (englisch).
8. On-Line Encyclopedia of Integer Sequences: Sequence A114865. Dezimalentwicklung des Wertes des eindeutigen, lokalen Maximums der Riemann-Siegelschen Theta-Funktion (englisch).
9. Harold Edwards: Riemann’s Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9, Abschnitt 6.5, S. 120 (englisch).
10. On-Line Encyclopedia of Integer Sequences: Sequence A036282. Zähler der asymptotischen Entwicklung der Theta-Funktion (englisch).
11. On-Line Encyclopedia of Integer Sequences: Sequence A114721. Nenner der asymptotischen Entwicklung der Theta-Funktion (englisch).
12. Harold Edwards: Riemann’s Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9, Abschnitt 6.5, S. 119 und 120 (englisch).
13. Harold Edwards: Riemann’s Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9, Abschnitt 6.3, S. 109 (englisch).
14. Anatoly A. Karatsuba, Sergei M. Voronin: The Riemann Zeta-Function. Walter de Gruyter, Berlin 1992, ISBN 3-11-013170-6, Kapitel I, Paragraph 6, Abschnitt 1, Theorem 1, S. 22 (englisch).
15. Peter Borwein et al.: The Riemann Hypothesis. Springer, New York 2008, ISBN 978-0-387-72125-5, Abschnitt 3.3, S. 31 (englisch).
16. Edward C. Titchmarsh: The Theory of the Riemann Zeta-Function. Oxford University Press, New York 1951, Reprint 2007, ISBN 978-0-19-853369-6, Abschnitt 9.2, S. 211 (englisch).
17. Harold Edwards: Riemann’s Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9, Abschnitt 6.5, S. 125 (englisch).
18. Peter Borwein et al.: The Riemann Hypothesis. Springer, New York 2008, ISBN 978-0-387-72125-5, Abschnitt 3.5, S. 33 (englisch).
19. John Irwin Hutchinson: On the roots of the Riemann zeta function. In: Trans. Amer. Math. Soc. Band 27, S. 49–60, 1925, bzgl. Grams Gesetz siehe S. 52 (englisch).

Anmerkungen

1. Die Gammafunktion besitzt Polstellen an allen nicht-positiven, ganzen Zahlen, also in 0, −1, −2, −3 usw. In der Definition der Theta-Funktion mit reellem ${\displaystyle \textstyle t}$ stellt dies allerdings kein Problem dar, da dann der Ausdruck ${\displaystyle \textstyle {\frac {2it+1}{4}}}$ diese Werte nicht annimmt. Vielmehr handelt es sich bei ${\displaystyle \textstyle {\frac {2it+1}{4}}}$, ${\displaystyle \textstyle t\in \mathbb {R} }$, um diejenige senkrechte Gerade in der komplexen Ebene, die durch den Punkt ${\displaystyle \textstyle {\frac {1}{4}}}$ verläuft.
2. Abseits ihrer Polstellen liefert die Gammafunktion komplexe, auch nicht-reelle, Zahlen als Funktionswerte. Argumente komplexer Zahlen ungleich 0 sind stets reell. Da der Ausdruck ${\displaystyle \textstyle {\frac {\log \pi }{2}}t}$ für reelles ${\displaystyle \textstyle t}$ ohnehin reell ist, handelt es sich bei der Theta-Funktion mit reellem Argument um eine reellwertige Funktion.
3. Argumente komplexer Zahlen ungleich 0 sind nur bis auf ganzzahlige Vielfache von ${\displaystyle \textstyle 2\pi }$ eindeutig. Für ${\displaystyle \textstyle t=0}$ ist ${\displaystyle \textstyle {\frac {\log \pi }{2}}t=0}$ und ${\displaystyle \textstyle \Gamma \left({\frac {2it+1}{4}}\right)=\Gamma \left({\frac {1}{4}}\right)\approx 3{,}6256\dots }$ eine reelle Zahl. Deshalb bedeutet die Bedingung ${\displaystyle \textstyle \theta (0)=0}$, dass in ${\displaystyle \textstyle t=0}$ für das Argument von ${\displaystyle \textstyle \Gamma \left({\frac {2it+1}{4}}\right)}$ der Wert 0 zu wählen ist, und eben nicht ${\displaystyle \textstyle 2\pi }$ oder ${\displaystyle \textstyle -18\pi }$ oder irgendein anderes ganzzahliges, von 0 verschiedenes Vielfaches von ${\displaystyle \textstyle 2\pi }$.
4. Die Stetigkeitsbedingung ist für die Teilfunktion ${\displaystyle \textstyle {\frac {\log \pi }{2}}t}$ erfüllt, da es sich hierbei um eine Gerade handelt. Die Gammafunktion ist abseits ihrer Polstellen holomorph, also insbesondere stetig. Damit ist sie auch entlang der Geraden ${\displaystyle \textstyle {\frac {2it+1}{4}}}$ stetig. Ausgehend von der Festlegung ${\displaystyle \textstyle \theta (0)=0}$, also ${\displaystyle \textstyle \arg \Gamma \left({\frac {2it+1}{4}}\right)=0}$, lassen sich daher die Werte der Argumentfunktion stets so wählen, dass die Funktion ${\displaystyle \textstyle \arg \Gamma \left({\frac {2it+1}{4}}\right)}$ und somit ${\displaystyle \textstyle \theta }$ stetig werden, und jene Werte sind durch diese Stetigkeitsbedingung eindeutig bestimmt.
5. Logarithmen von komplexen Zahlen ungleich 0 sind nur bis auf ganzzahlige Vielfache von ${\displaystyle \textstyle 2\pi i}$ eindeutig. Die Festlegung auf den Hauptzweig des Logarithmus führt dazu, dass ${\displaystyle \textstyle \theta }$ stetig ist und für ${\displaystyle \textstyle t=0}$ gilt:

   ${\displaystyle \textstyle \operatorname {Im} \log \Gamma \left({\frac {2it+1}{4}}\right)=\operatorname {Im} \log \Gamma \left({\frac {1}{4}}\right)=\operatorname {Im} \log \left(3{,}6256\dots \right)=0}$.

   Hätte man nicht den Hauptzweig des Logarithmus gewählt, sondern einen anderen Zweig, so wäre im letzten Schritt dieser Gleichung ${\displaystyle \textstyle \log \left(3{,}6256\dots \right)=2k\pi i}$ mit einem ganzzahligen ${\displaystyle \textstyle k}$ ungleich 0. Dann wäre aber ${\displaystyle \textstyle \operatorname {Im} \log \left(3{,}6256\dots \right)=2k\pi \neq 0}$ und somit auch ${\displaystyle \textstyle \theta (0)\neq 0}$.
6. Anstelle von ${\displaystyle \textstyle 0\leq \sigma \leq 1}$ wird der kritische Streifen auch häufig als die Menge aller komplexen Zahlen mit Realteil ${\displaystyle \textstyle 0<\sigma <1}$ definiert, da nach dem Primzahlsatz ohnehin keine Nullstellen der Zeta-Funktion auf den beiden senkrechten Geraden durch 0 bzw. 1 liegen. Von diesen beiden Geraden ist also bekannt, dass sie nicht „kritisch“ sind. Deshalb sind sie bei der Definition des kritischen Streifens verzichtbar.