Liste nicht-trivialer Nullstellen der Riemannschen Zetafunktion
Die nachfolgende Tabelle listet die ersten 50 nicht-trivialen Nullstellen der Riemannschen Zetafunktion auf.
Erklärung
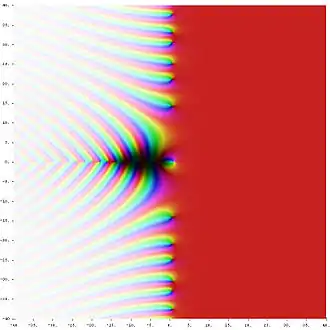
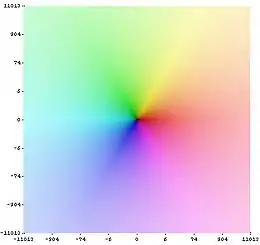
Die Menge aller komplexen Nullstellen der Riemannschen Zetafunktion zerfällt in zwei Teilmengen: in die Teilmenge der sogenannten trivialen Nullstellen, welche die Riemannsche Zetafunktion an den negativen geraden Zahlen (−2, −4, −6, −8 usw.) annimmt, und in die Teilmenge der sogenannten nicht-trivialen Nullstellen, deren Realteil zwischen 0 und 1 liegt. Die bis heute weder bewiesene noch widerlegte Riemannsche Vermutung aus dem Jahr 1859 besagt, dass alle nicht-trivialen Nullstellen der Riemannschen Zetafunktionen den Realteil 1/2 besitzen.
Zu den überwältigend vielen, nicht-trivialen Nullstellen der Riemannschen Zetafunktion, von denen bekannt ist, dass sie tatsächlich den Realteil 1/2 besitzen, zählen die in der nachfolgenden Tabelle angegebenen Nullstellen. Deshalb werden in der zweiten Spalte der Tabelle nur die Imaginärteile der nicht-trivialen Nullstellen angegeben. Der zugehörende Realteil ist stets 1/2.
Die unendlich vielen, nicht-trivialen Nullstellen sind spiegelsymmetrisch zur reellen Achse angeordnet. Besitzt also in nachfolgender Tabelle eine nicht-triviale Nullstelle den Imaginärteil , so ist auch die zu komplex konjugierte Zahl eine nicht-triviale Nullstelle der Riemannschen Zetafunktion (dabei bezeichnet die imaginäre Einheit). Aus diesem Grund werden in der nachfolgenden Tabelle keine nicht-trivialen Nullstellen mit negativem Imaginärteil aufgelistet. Bei den Imaginärteilen in der zweiten Spalte werden 30 Nachkommastellen angegeben. Die letzte angegebene Nachkommastelle ist nicht gerundet.
Die Nummerierung der nicht-trivialen Nullstellen in der ersten Spalte folgt steigenden Werten der Imaginärteile der Nullstellen. Es ist also die nicht-triviale Nullstelle der Riemannschen Zetafunktion mit dem kleinsten, positiven Imaginärteil. Die nicht-triviale Nullstelle besitzt den zweitkleinsten, positiven Imaginärteil usw.
Die einfachste Methode zur numerischen Berechnung nicht-trivialer Nullstellen der Zetafunktion verwendet die Euler-Maclaurin-Formel.[1] Mit ihrer Hilfe konnte der dänische Mathematiker Gram bis 1903 die ersten 15 nicht-trivialen Nullstellen mit einer Genauigkeit von wenigen Dezimalstellen berechnen.[2]
Fortgeschrittene Methoden stützen sich auf die Riemann-Siegelsche Z-Funktion. Die Nullstellen dieser reellwertigen Funktion reellen Arguments stimmen mit den Imaginärteilen der Nullstellen der Zetafunktion mit Realteil 1/2 überein. Bei der Berechnung der Nullstellen der Z-Funktion kommen die Riemann-Siegelsche Formel und die asymptotische Entwicklung der Riemann-Siegelschen Theta-Funktion zum Einsatz. Zusammen mit der Kenntnis der Anzahl der nicht-trivialen Nullstellen im betrachteten Intervall des Imaginärteils lässt sich dann prüfen, ob die berechneten Nullstellen der Zeta-Funktion mit einem Realteil von 1/2 schon alle nicht-trivialen Nullstellen in diesem Intervall erfassen[3]. Auch das Verfahren von Odlyzko und Schönhage basiert auf der Z-Funktion. Im Vergleich zu älteren Verfahren, die die Z-Funktion einsetzen, steigert es seine Geschwindigkeit z. B. durch den Einsatz schneller Fourier-Transformationen.[4]
Tabelle
| n | Imaginärteil |
|---|---|
| 1 | 14,134725141734693790457251983562… |
| 2 | 21,022039638771554992628479593896… |
| 3 | 25,010857580145688763213790992562… |
| 4 | 30,424876125859513210311897530584… |
| 5 | 32,935061587739189690662368964074… |
| 6 | 37,586178158825671257217763480705… |
| 7 | 40,918719012147495187398126914633… |
| 8 | 43,327073280914999519496122165406… |
| 9 | 48,005150881167159727942472749427… |
| 10 | 49,773832477672302181916784678563… |
| 11 | 52,970321477714460644147296608880… |
| 12 | 56,446247697063394804367759476706… |
| 13 | 59,347044002602353079653648674992… |
| 14 | 60,831778524609809844259901824524… |
| 15 | 65,112544048081606660875054253183… |
| 16 | 67,079810529494173714478828896522… |
| 17 | 69,546401711173979252926857526554… |
| 18 | 72,067157674481907582522107969826… |
| 19 | 75,704690699083933168326916762030… |
| 20 | 77,144840068874805372682664856304… |
| 21 | 79,337375020249367922763592877116… |
| 22 | 82,910380854086030183164837494770… |
| 23 | 84,735492980517050105735311206827… |
| 24 | 87,425274613125229406531667850919… |
| 25 | 88,809111207634465423682348079509… |
| 26 | 92,491899270558484296259725241810… |
| 27 | 94,651344040519886966597925815208… |
| 28 | 95,870634228245309758741029219246… |
| 29 | 98,831194218193692233324420138622… |
| 30 | 101,317851005731391228785447940292… |
| 31 | 103,725538040478339416398408108695… |
| 32 | 105,446623052326094493670832414111… |
| 33 | 107,168611184276407515123351963086… |
| 34 | 111,029535543169674524656450309944… |
| 35 | 111,874659176992637085612078716770… |
| 36 | 114,320220915452712765890937276191… |
| 37 | 116,226680320857554382160804312064… |
| 38 | 118,790782865976217322979139702699… |
| 39 | 121,370125002420645918945532970499… |
| 40 | 122,946829293552588200817460330770… |
| 41 | 124,256818554345767184732007966129… |
| 42 | 127,516683879596495124279323766906… |
| 43 | 129,578704199956050985768033906179… |
| 44 | 131,087688530932656723566372461501… |
| 45 | 133,497737202997586450130492042640… |
| 46 | 134,756509753373871331326064157169… |
| 47 | 138,116042054533443200191555190282… |
| 48 | 139,736208952121388950450046523382… |
| 49 | 141,123707404021123761940353818475… |
| 50 | 143,111845807620632739405123868913… |
Literatur
Die Fachliteratur zur Mathematik der Riemannschen Zetafunktion und ihrer Nullstellen wurde zu einem großen Teil in englischer Sprache verfasst. Es existiert vergleichsweise wenig deutschsprachige Literatur zu diesem Thema.
- Tom M. Apostol: Introduction to Analytic Number Theory. Springer, New York 1976, ISBN 0-387-90163-9 (Insbesondere Kapitel 11, 12 und 13).
- Peter Borwein, Stephen Choi, Brendan Rooney, Andrea Weirathmueller: The Riemann Hypothesis. Springer, New York 2008, ISBN 978-0-387-72125-5 (Insbesondere Kapitel 2 und 3.).
- Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin, Heidelberg 1995, ISBN 3-540-58821-3.
- John Brian Conrey: More than two fifths or the zeros of the Riemann zeta function are on the critical line. In: Journal für die reine und angewandte Mathematik (Crelles Journal). Band 1989, Nr. 399. Walter de Gruyter, Berlin, New York 1989, S. 1–26.
- Harold Edwards: Riemann’s Zeta Function. Dover, 2001, ISBN 0-486-41740-9 (Dieses Buch erläutert ausführlich die Mathematik in Bernhard Riemanns berühmter Originalarbeit "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse" aus dem Jahr 1859. Es enthält im Anhang eine englische Übersetzung dieser Originalarbeit.).
- Aleksandar Ivić: The Riemann Zeta-Function: theory and applications. Dover, Mineola 2003, ISBN 0-486-42813-3.
- Henryk Iwaniec, Emmanuel Kowalski: Analytic Number Theory. American Mathematical Society, Providence 2004, ISBN 0-8218-3633-1 (Insbesondere Kapitel 1 und 5).
- Eugen Jahnke: Tafeln höherer Funktionen. Teubner, Stuttgart 1966.
- Anatoly A. Karatsuba, S. M. Voronin: The Riemann Zeta-Function. Walter de Gruyter, Berlin 1992, ISBN 3-11-013170-6.
- Peter Meier, Jörn Steuding: Wer die Zetafunktion kennt, kennt die Welt! In: Spektrum der Wissenschaft Dossier 6/2009: „Die größten Rätsel der Mathematik“. ISBN 978-3-941205-34-5, S. 12–19.
- Jürgen Neukirch: Algebraische Zahlentheorie. Springer, Berlin 1992, ISBN 3-540-54273-6 (Insbesondere Kapitel 7).
- Samuel Patterson: An introduction to the theory of the Riemann Zeta-Function. Cambridge University Press, New York 1995, ISBN 0-521-49905-4.
- Paulo Ribenboim: Die Welt der Primzahlen. 2. Auflage. Springer, Berlin, Heidelberg 2011, ISBN 978-3-642-18078-1 (Insbesondere Kapitel 4, Abschnitt I.).
- Bernhard Riemann: Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse. In: Monatsberichte der Königlichen Preußischen Akademie der Wissenschaften zu Berlin. Berlin 1859, S. 671–680 (Wikisource).
- Atle Selberg: On the zeros of the Riemann zeta-function. In: Skr. Norske Vid. Akad. Oslo. Band 10, 1942, S. 1–59.
- Edward Charles Titchmarsh: The Theory of the Riemann Zeta-Function. 1951.
- Sergei Michailowitsch Woronin: Theorem on the 'universality' of the Riemann zeta-function. In: Mathematics of the USSR-Izvestiya. Band 9, Nr. 3, 1975, S. 443–445.
Numerische Berechnung nicht-trivialer Nullstellen der Riemannschen Zetafunktion:
- Richard P. Brent: On the zeros of the Riemann zeta function in the critical strip. In: Mathematics of Computation. Band 33, Nr. 148, 1979, ISSN 0025-5718, S. 1361–1372, doi:10.1090/S0025-5718-1979-0537983-2 (englisch, ams.org).
- R. P. Brent, J. van de Lune, H. J. J. te Riele, D. T. Winter: On the zeros of the Riemann zeta function in the critical strip. II. In: Mathematics of Computation. Band 39, Nr. 160, 1982, ISSN 0025-5718, S. 681–688, doi:10.1090/S0025-5718-1982-0669660-1 (englisch, ams.org).
- J. van de Lune, H. J. J. te Riele: On the zeros of the Riemann zeta function in the critical strip. III. In: Mathematics of Computation. Band 41, Nr. 164, 1983, ISSN 0025-5718, S. 759–767, doi:10.1090/S0025-5718-1983-0717719-3 (englisch, ams.org).
- J. van de Lune, H. J. J. te Riele, D. T. Winter: On the zeros of the Riemann zeta function in the critical strip. IV. In: Mathematics of Computation. Band 46, Nr. 174, 1986, ISSN 0025-5718, S. 667–681, doi:10.1090/S0025-5718-1986-0829637-3 (englisch, ams.org).
Weblinks
- The LMFDB Collaboration (L-functions and Modular Forms Database): Zeros of zeta(s). Abgerufen am 8. Juni 2018 (englisch, Online-Berechnung nicht-trivialer Nullstellen der Riemannschen Zetafunktion).
- Andrew Odlyzko: Table of zeros of the Riemann zeta function. Abgerufen am 8. Juni 2018 (englisch).
- Gleb Beliakov, Yuri Matiyasevich (2013): Zeroes of Riemann's zeta function on the critical line with 40000 decimal digits accuracy (1,48 GB)
Einzelnachweise
- Harold Edwards: Riemann's Zeta Function, Dover, Mineola, 2001, ISBN 0-486-41740-9, Abschnitte 6.1–6.4, S. 96–118 (englisch).
- Andrew Odlyzko: The 1022-nd zero of the Riemann zeta function (PDF; 178 kB). In: M. van Frankenhuysen, M. L. Lapidus (Hrsg.): Dynamical, Spectral, and Arithmetic Zeta Functions. ( = Contemporary Mathematics. Nr. 290). American Mathematical Society, 2001, ISBN 0-8218-5626-X, S. 139–144 (englisch).
- Andrew Odlyzko: Analytic Computations in Number Theory (PDF; 188 kB). In: W. Gautschi (Hrsg.): Mathematics of Computation 1943–1993: A Half-Century of Computational Mathematics (= Proceedings of symposia in applied mathematics. Nr. 48). American Mathematical Society, 1994, ISBN 0-8218-0291-7, S. 451–463 (englisch).
- Andrew Odlyzko, Arnold Schönhage: Fast Algorithms for multiple evaluations of the Riemann zeta function (PDF; 1,2 MB). In: Transactions of the American Mathematical Society. Band 309, Nr. 2, 1988, S. 797–809 (englisch).