Rekurrenzplot
Ein Rekurrenzplot (von lateinisch recurrere „wiederkehren“) ist eine moderne Methode der nichtlinearen Datenanalyse. Die Wiederkehr-Eigenschaft ist typisch für deterministische dynamische Systeme (Chaos, nichtlineare Dynamik) und spiegelt sich auch in vielen natürlichen Prozessen wider, wie z. B. El Niño, Milanković-Zyklen oder Sonnenflecken-Zyklen. Wiederkehr bedeutet dabei nicht, dass ganz genau der ursprüngliche Zustand wieder eintritt, sondern dass er nur beliebig genau wieder getroffen wird. Bereits Poincaré hatte die unendliche Wiederkehr von Zuständen postuliert.
Die Methode der Rekurrenzplots wurde 1987 von Eckmann eingeführt. Sie dient zur Darstellung von höherdimensionalen Phasenraum-Trajektorien.
Beschreibung
Der Rekurrenzplot ist eine quadratische Matrix mit zwei Zeitachsen. In dieser Matrix sind durch schwarze Punkte diejenigen Zeitpaarungen dargestellt, deren Zustände nahezu gleich sind, d. h. wann der entsprechende Zustand wiedergekehrt ist. Die Wiederkehr wird in der Regel aus der Distanz zwischen allen Paarungen der Daten bestimmt:
Hierbei ist die Heaviside-Funktion, der Maximalabstand und eine Norm, beispielsweise die Euklidische Norm.
Das Aussehen des Rekurrenzplots wird durch das Verhalten der Phasenraum-Trajektorie bestimmt. Dabei unterscheidet man zwischen den kleinen Strukturen, wie Einzelpunkte, Diagonallinien oder Vertikallinien, und dem Gesamteindruck des Plots (Textur).
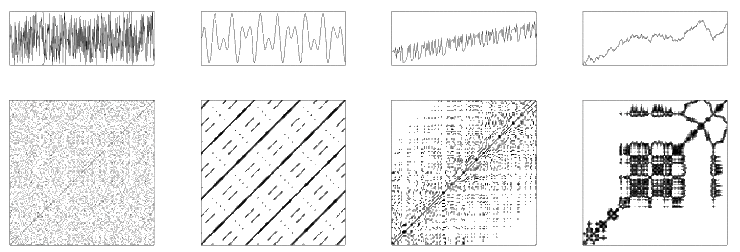
Neuere Entwicklungen erlauben eine weitergehende Untersuchung von Daten durch eine quantitative Auswertung von Rekurrenzplots (Zbilut und Webber, 1992; Marwan et al., 2002).
Ein Close Returns Plot ist ein Rekurrenzplot mit einer etwas anderen Art der Auftragung von Wiederkehr-Zeiten. Hier entspricht die y-Achse nicht der absoluten Zeit, sondern der Zeitdifferenz (also, nach welcher Zeit der Zustand wiederkehrt).
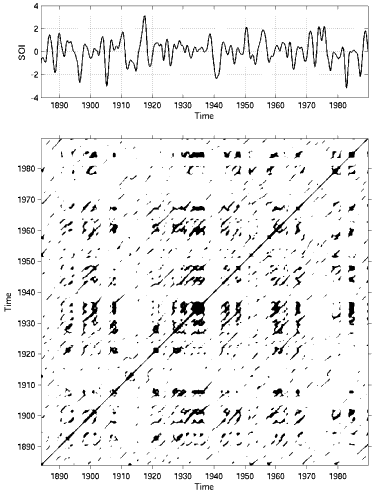
Literatur
- J. P. Eckmann, S. O. Kamphorst, D. Ruelle: Recurrence Plots of Dynamical Systems. In: Europhysics Letters. 5, 1987, S. 973–977. doi:10.1209/0295-5075/4/9/004.
- N. Marwan, M. C. Romano, M. Thiel, J. Kurths: Recurrence Plots for the Analysis of Complex Systems. In: Physics Reports. 438, Nr. 5–6, 2007. doi:10.1016/j.physrep.2006.11.001.
- N. Marwan: A historical review of recurrence plots. In: The European Physical Journal - Special Topics. 164, Nr. 1, 2008, S. 3–12. doi:10.1140/epjst/e2008-00829-1.