Raised-Cosine-Filter

Das Raised-Cosine-Filter, auch als Kosinus-Roll-off-Filter bezeichnet, ist ein in der digitalen Signalverarbeitung, einem Teilbereich der Nachrichtentechnik, angewandtes elektronisches Filter, das zur Formung von Signalimpulsen verwendet wird. Es gehört zu der Gruppe der Nyquist-Filter.

Als wesentliche Eigenschaft erfüllt dieses Filter die erste Nyquistbedingung. Dies bedeutet, dass zeitlich aufeinanderfolgende Signalimpulse, die mit diesem Filter geformt werden, im Zeitraster des Abtastsignals Nullstellen besitzen und damit vorausgehende und nachfolgende Impulse zu den Abtastzeitpunkten nicht beeinträchtigen. Damit erlaubt dieses Filter eine zeitlich diskrete Signalübertragung, in der keine Intersymbolinterferenz (ISI) auftritt.

Darstellung

Ein Raised-Cosine-Filter weist immer die Eigenschaften eines Tiefpasses auf und wird in digitalen Filterstrukturen (etwa als Filter mit endlicher Impulsantwort (FIR)) realisiert. Seine Übertragungsfunktion (der Betrag des Frequenzganges) ist bis zu einer bestimmten Frequenz, die von einem Roll-off-Faktor abhängt, konstant und fällt darüber hinaus für höhere Frequenzen kosinusförmig bis auf den Wert Null ab. Aus diesem Umstand leitet sich auch die Bezeichnung dieses Filters ab.

Das Raised-Cosine-Filter wird bei digitalen Signalübertragungen zur Formung der am Übertragungskanal verwendeten Sendeimpulse verwendet. Die Sendeimpulse, oder auch Symbole genannt, stellen die diskrete, zu übertragene Information dar. Der Übertragungskanal kann beispielsweise ein Funkkanal oder auch leitungsgebunden sein. Anwendungen liegen daher bei digitalen Übertragungen wie beispielsweise im Mobilfunkbereich.

Die Implementierung dieses Filters erfolgt in digitalen Signalprozessoren (DSP), anwendungsspezifischen integrierte Schaltungen (ASIC) oder frei programmierbaren digitalen Schaltungen, den so genannten Field Programmable Gate Arrays (FPGA).

Übertragungsfunktion

Die Übertragungsfunktion dieses Filters ist, abgesehen von der bei zeitdiskreten Übertragungssystemen immer wesentlichen Symbolrate (1/T), von einem speziellen Faktor, dem Roll-off-Faktor α, abhängig. Die Bezeichnung α für den Roll-off-Faktor ist in der Literatur nicht einheitlich gewählt. Es kommen auch Bezeichnungen wie r oder β vor.

Mit diesem Faktor, der Werte zwischen 0 und 1 annehmen kann, wird die Steilheit der Übertragungskennlinie wesentlich beeinflusst: Für den Grenzwert α = 0 ergibt sich ein idealer, nicht kausaler Tiefpass mit rechteckförmiger Übertragungsfunktion. Für α = 1 ergibt sich eine maximal flache Kosinusflanke. Für Zwischenwerte ist der dazugehörige Frequenzgang in einem bestimmten Bereich annähernd konstant und fällt erst dann mit einer etwas steileren Kosinusflanke ab, wie in nachfolgenden Abbildungen dargestellt:

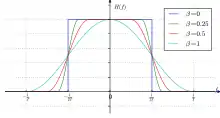Betragsverlauf der Übertragungsfunktion mit unterschiedlichen Roll-off-Faktoren β

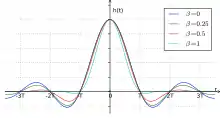Impulsantwort mit unterschiedlichen Roll-off-Faktoren β

Je größer der Roll-off-Faktor ist, desto mehr nimmt die Bandbreite des Filters zu. Die Bandbreite kann (aufgrund der zeitdiskreten Eigenschaft) nur maximal bis zur Symbolrate 1/T zunehmen. Ein kleinerer Roll-off-Faktor führt, aufgrund der steiler werdenden Filterflanke, zu größeren unerwünschten Überschwingungen, die letztlich in realen Übertragungssystemen ein größeres Phasenrauschen und damit eine unzureichende Pulsformung bewirken. Das kann zu Fehlern in der Demodulation führen.

In der Praxis wird dennoch meist ein Roll-off-Faktor unter 0,5 im Bereich von 0,2 bis 0,5 verwendet, da dadurch kostbare Bandbreite eingespart werden kann. So verwendet beispielsweise der Mobilfunkstandard UMTS für die darin verwendeten Impulsfilter einen Roll-off-Faktor von α = 0,22.

Die Bandbreite des Filters mit der Symbolrate f_s = 1/T berechnet sich im Basisband zu:

B={\frac {1}{2}}\left(1+\alpha \right)\cdot f_{s}

Mathematische Beschreibung der Übertragungsfunktion

Die auf 1 normierte Übertragungsfunktion H(f) ist gegeben durch

H(f)={\begin{cases}1,&|f|\leq {\frac {1-\alpha }{2T}}\\\cos ^{2}\left({\frac {\pi T}{2\alpha }}\left(|f|-{\frac {1-\alpha }{2T}}\right)\right),&{\frac {1-\alpha }{2T}}<|f|\leq {\frac {1+\alpha }{2T}}\\0,&{\textrm {sonst}}\end{cases}}

mit der Impulsantwort

h(t)={\begin{cases}1,&t=0\\{\frac {\sin(\pi /(2\alpha ))}{\pi /(2\alpha )}}{\frac {\pi }{4}},&|t|={\frac {T}{2\alpha }}\\{\frac {\sin(\pi t/T)}{\pi t/T}}{\frac {\cos(\alpha \pi t/T)}{1-(2\alpha t/T)^{2}}},&{\textrm {sonst}}\\\end{cases}}

,

wobei die Singularitäten bei $t=0$ und $|t|=T/(2\alpha )$ durch stetige Fortsetzung behoben wurden. Die Impulsantwort weist den Verlauf der si-Funktion auf, die bei Vielfachen der Symboldauer T Nullstellen hat und damit frei von Intersymbolinterferenz ist.

Symbolrate

Die übertragbare Symbolrate eines Raised-Cosine-Filters bei gegebenen Roll-off-Faktors α und einer Bandbreite B beträgt:

f_{s}={\frac {1}{T}}={\frac {2B}{1+\alpha }}

Da im Bandpassbereich die doppelte Bandbreite (aufgrund des Entstehens von zwei Seitenbändern vgl. Amplitudenmodulation) eingenommen wird ergibt sich:

f_{s}={\frac {B_{\mathrm {HF} }}{1+\alpha }}

Im Basisband liegt die Bandbreiteneffizienz im Grenzfall von α=0 bei 2 Symbole/s pro Hertz Bandbreite bzw. bei binärer Übertragung 2 Bit/s pro Hertz Bandbreite und halbiert sich bei doppeltem Bandbreitenbedarf im Bandpassbereich. Bei praktischen Realisierungen werden Roll-off-Faktoren im Bereich α=0,3 (30 %) gewählt, wodurch sich bei binärer Übertragung eine spektrale Effizienz von ca. 1,5 Bit/s pro Hertz Bandbreite ergibt.

Augendiagramm

Die folgenden Abbildungen zeigen Augendiagramme von Raised-Cosine-Filtern mit verschiedenen Roll-off-Faktoren. Mit diesem lässt sich die Qualität der Signale beurteilen.

Roll-off-Faktor 0 (idealer Tiefpass)

Roll-off-Faktor 0,25

Root-Raised-Cosine-Filter

Das Root-Raised-Cosine-Filter, kurz RRC, entspricht der Wurzel (engl. root) aus dem Raised-Cosine-Filter.

Siehe auch

Adjacent Channel Power

Literatur

John B. Anderson: Digital Transmission Engineering. 2. Auflage. Wiley Interscience, Lund, Schweden 2005, ISBN 0-471-69464-9.
Kaveh Pahlavan, Allen H. Levesque: Wireless Information Networks. 2. Auflage, John Wiley & Sons Ltd, New Jersey 2005, ISBN 978-0-471-72542-8.
Amithaba Bhattacharya: Dig Communication. Tata McGraw Hill Education Privat Limited, New Delhi 2006, ISBN 0-07-059117-2.
Eduard Säckinger: Broadband Circuits for Optical Fiber Communication. John Wiley & Sons Ltd, New Jersey 2005, ISBN 0-471-71233-7.
John Dunlop, Demessie Girma, James Irvine: Digital Mobile Communications and the TETRA System. John Wiley & Sons Ltd, Chychester 1999, ISBN 0-471-98792-1.

Weblinks

F. Dellsperger: Passive Filter. 2004 (Memento vom 24. November 2013 im Internet Archive; PDF; 544 kB) – gute Informationen über passive Filter.
Information über RC- und RRC-Filter
Beispiel Raised-Cosine-Filter 7. Ordnung
Monolithisch integrierte Empfängerschaltung (PDF, 3,3 MB)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.