Root-Raised-Cosine-Filter

Das Root-Raised-Cosine-Filter, abgekürzt RRC-Filter, ist ein in der digitalen Signalverarbeitung angewandtes elektronisches Filter, welches zur Formung von Signalimpulsen zur Übertragung über einen Kanal, wie beispielsweise einen Funkkanal, verwendet wird.

Allgemeines

Das Root-Raised-Cosine-Filter entspricht der Wurzel (engl. root) aus dem Raised-Cosine-Filter und dient dazu, die Charakteristik des Raised-Cosine auf Sender und Empfänger gleichmäßig zu verteilen. Es stellt dann ein so genanntes Matched Filter dar und maximiert im Empfänger das Signal-Rausch-Verhältnis. Eine Besonderheit ist, dass ein Root-Raised-Cosine-Filter für sich alleine Intersymbolinterferenz (ISI) aufweist, das heißt die einzelnen Sendeimpulse „fließen“ am Übertragungskanal zeitlich ineinander. Erst die Kombination der beiden RRC-Filter bei Sender und Empfänger ergeben zusammen über die gesamte Strecke im Idealfall eine ISI-freie Übertragungsstrecke, welche eine zeitliche Unterscheidung der einzelnen Impulse erlaubt. Die einzelnen RRC-Impulse stehen orthogonal zueinander.

Das Root-Raised-Cosine-Filter ist neben dem Gauß-Filter eines der am häufigsten eingesetzten Filter zur Impulsformung bei digitalen Übertragungssystemen.

Übertragungsfunktion

Impulsantwort h(t) eines RRC für verschiedene roll-off-Faktoren β

Der Betragsverlauf der Übertragungsfunktion H_rrc(jω) eines RRC-Filters ist gegeben durch:

|H_{\mathrm {RRC} }(j\omega )|={\sqrt {|H_{\mathrm {RC} }(j\omega )|}}

wobei H_rc(jω) die Übertragungsfunktion des Raised-Cosine-Filters darstellt.

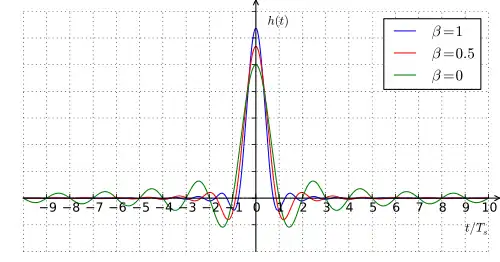
Die Impulsantwort h(t) eines RRC-Filters ist durch den Roll-off-Faktor β, welcher die Bandbreite bestimmt, und die Dauer eines Sendesymbols T_s gekennzeichnet und besitzt folgende Form:

h(t)={\begin{cases}{\dfrac {1}{\sqrt {T_{s}}}}\left(1-\beta +4{\dfrac {\beta }{\pi }}\right),&t=0\\{\dfrac {\beta }{\sqrt {2T_{s}}}}\left[\left(1+{\dfrac {2}{\pi }}\right)\sin \left({\dfrac {\pi }{4\beta }}\right)+\left(1-{\dfrac {2}{\pi }}\right)\cos \left({\dfrac {\pi }{4\beta }}\right)\right],&t=\pm {\dfrac {T_{s}}{4\beta }}\\{\dfrac {1}{\sqrt {T_{s}}}}{\dfrac {\sin \left[\pi {\dfrac {t}{T_{s}}}\left(1-\beta \right)\right]+4\beta {\dfrac {t}{T_{s}}}\cos \left[\pi {\dfrac {t}{T_{s}}}\left(1+\beta \right)\right]}{\pi {\dfrac {t}{T_{s}}}\left[1-\left(4\beta {\dfrac {t}{T_{s}}}\right)^{2}\right]}},&{\mbox{andernfalls}}\end{cases}}

Beispiel-Implementierung

Nachfolgend findet sich eine Beispiel-Implementierung des RRC-Filters in Python mit Hilfe von NumPy, wobei die dafür verwendete Formel aus[1] entnommen wurde.

import numpy as np


def rrcosfilter(N, beta, Ts, Fs):
    "" target="_blank" rel="nofollow""
    Erzeugt ein Root-Raised-Cosine-Filter, welches symmetrisch zum Mittelpunkt
    verläuft.
    Parameter:
    -----------
    N : int
        Anzahl der Filterpunkte.
    beta : float
        Roll-Off Faktor im Intervall [0, 1].
    Ts : float
        Die Symbolperiode (inverse der Symbolrate) in Sekunden.
    Fs : float
        Die Abtastrate in Hertz.
    Rückgabe:
    -----------
    h_rcc : numpy.ndarray
        Die Impulsantwort des Filters als NumPy-Array.
    "" target="_blank" rel="nofollow""

    T_delta = 1/float(Fs)
    sample_num = np.arange(N)
    h_rrc = np.zeros(N, dtype=float)

    for x in sample_num:
        t = (x-N/2)*T_delta
        if t == 0.0:
            scaling = 1/np.sqrt(Ts)
            equation = 1-beta+(4*beta/np.pi)
            h_rrc[x] = scaling * equation
        elif beta != 0 and t == (Ts/(4*beta) or -Ts/(4*beta)):
            scaling = beta/np.sqrt(2*Ts)
            equation = (1+(2/np.pi))*np.sin(np.pi/(4*beta)) + (1-2/np.pi)*np.cos(np.pi/(4*beta))
            h_rrc[x] = scaling * equation
        else:
            scaling = 1/np.sqrt(Ts)
            numerator = np.sin(np.pi*(1-beta)*t/Ts) + (4*beta*t/Ts)*np.cos(np.pi*(1+beta)*t/Ts)
            denominator = (np.pi*t/Ts)*(1-np.square(4*beta*t/Ts))
            equation = numerator / denominator
            h_rrc[x] = scaling * equation
    return h_rrc

sample_rrc = rrcosfilter(N=189, beta=0.22, Ts=1e-5, Fs=100e6)

Literatur

John G. Proakis, Masoud Salehi: Communication Systems Engineering. 2. Auflage. Prentice Hall, Upper Saddle River NJ 2002, ISBN 0-13-095007-6.
John B. Anderson: Digital Transmission Engineering. 2. Auflage. Wiley-Interscience, 2005, ISBN 0-471-69464-9, S. 26–30.

Einzelnachweise

John B. Anderson: Digital transmission engineering. Piscataway, New Jersey 2005, ISBN 1-280-31132-0.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] John B. Anderson: Digital transmission engineering. Piscataway, New Jersey 2005, ISBN 1-280-31132-0.