Symbolübersprechen
Das Symbolübersprechen, auch als Intersymbolinterferenz (ISI) bezeichnet, beschreibt bei digital kodierten Übertragungstechniken Störungen zwischen zeitlich aufeinanderfolgenden Sendesymbolen.
Im Gegensatz zum Übersprechen, welches ein gegenseitiges Übersprechen räumlich benachbarter Übertragungspfade beschreibt und auch analoge Übertragungen betreffen kann, betrifft das Symbolübersprechen die zeitliche Abfolge der zur digitalen Übertragung genutzten Symbole ein und desselben Übertragungskanals.
Ursachen
Bei einer digitalen Übertragung wird die wertdiskrete Information in zeitlich aufeinanderfolgenden Symbolen über einen Kanal übertragen. Dieser Kanal kann z. B. eine Funkstrecke oder eine kabelgebundene Übertragung sein. Symbolübersprechen wird dabei durch folgende Ursachen ausgelöst:
- Durch die Begrenzung der Bandbreite des Übertragungskanals. Dadurch kann die Form der Sendesymbole durch unterschiedliche Gruppenlaufzeiten der einzelnen Frequenzanteile spektral verformt und zeitlich gedehnt werden. Dadurch „fließen“ die einzelnen Symbole zeitlich ineinander.
- Mehrwegeausbreitung, insbesondere bei Freiraumverbindungen mit Echos. Hierbei kommt es durch unterschiedlich lange Laufzeiten der einzelnen Signalwege beim Empfänger zu einer zeitlich versetzten Überlagerung der gesendeten Symbole. Im Extremfall kann die Störung durch destruktive Interferenz Symbolfolgen zumindest zeitweise gänzlich auslöschen.
- Bei manchen Impulsformungsfiltern wie dem Root-Raised-Cosine-Filter wird bewusst eine Intersymbolinterferenz am Übertragungskanal zugelassen, mit dem Ziel die benötige Bandbreite zu minimieren. Dabei wird am Empfänger ein an die Pulsformung des Senders angepasstes Filter eingesetzt, so dass in Summe (d. h. beide Impulsformungsfilter und Übertragungsstrecke) eine ISI-freie Datenübertragung möglich ist.
Bandbegrenzte Kanäle
Da jeder Übertragungskanal eine Bandbegrenzung aufweist und andererseits ein Übertragungskanal möglichst effizient genutzt werden soll, ergeben sich bestimmte Grenzbedingungen, unter denen bei einer gegebenen Bandbreite noch eine ISI-freie Übertragung möglich ist. Diese sind in den beiden Nyquistbedingungen zusammengefasst, welche für das Vermeiden von Symbolübersprechen infolge einer Bandbegrenzung zu erfüllen sind.
Erste Nyquistbedingung
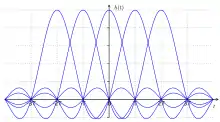
Die erste Nyquistbedingung besagt, dass die Impulsantwort h(t) des Gesamtübertragungssystems mit der Abtastrate T zu den Abtastzeitpunkten n·T (n ganzzahlig) folgende Bedingung erfüllen muss:
Dies bedeutet, dass ein bestimmtes Sendesymbol, welches zum Zeitpunkt n=0 gesendet wird, zu allen anderen Abtastzeitpunkten null sein muss.
Um diese Bedingung zu erfüllen, werden Impulsformungsfilter eingesetzt, z. B. der Raised-Cosine-Filter (RC-Impuls), dessen Impulsantwort rechts für eine Abfolge von fünf Sendeimpulsen dargestellt ist. Jeder RC-Impuls ist nur genau bei seinem Abtastzeitpunkt gleich 1 und zu allen anderen Abtastzeitpunkten gleich 0, womit kein Symbolübersprechen auftritt.
Als ein weiteres Beispiel erfüllt auch das ideale Tiefpassfilter die erste Nyquistbedingung, lässt sich aber aufgrund der fehlenden Kausalität nicht realisieren.
Zweite Nyquistbedingung
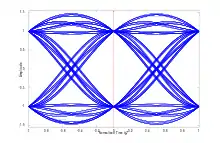
Die zweite Nyquistbedingung stellt eine Verschärfung der ersten dar, indem sie zusätzlich fordert, dass die Impulsantwort h(t) des Filters exakt zwischen zwei Abtastzeitpunkten den Wert 0 aufweisen muss.
Dieser Umstand kann im Augendiagramm grafisch verdeutlicht werden: Die erste Nyquistbedingung fordert die maximale Öffnung des Auges zum Abtastzeitpunkt t=0 in vertikaler Richtung. Die zweite Nyquistbedingung fordert die maximale Öffnung des Auges in horizontaler Richtung mit der Symboldauer T.
Im nebenstehenden Augendiagramm ist die zweite Nyquistbedingung knapp nicht erfüllt. Der RC-Impuls eines Raised-Cosine-Filters erfüllt nur für den roll-off-Faktor von β=1 die zweite Nyquistbedingung. In diesem Fall stellt die Signalflanke des RC-Impulses eine Nyquist-Flanke dar.
In vielen praktischen Übertragungssystemen wird die zweite Nyquistbedingung nicht exakt erfüllt. Je weniger die zweite Nyquistbedingung erfüllt ist bzw. je weiter das Auge in horizontaler Richtung geschlossen ist, desto genauer muss der Symboltakt am Empfänger sein.
Literatur
- Karl-Dirk Kammeyer: Nachrichtenübertragung. 4. neubearbeitete und ergänzte Auflage. Vieweg + Teubner, Wiesbaden 2008, ISBN 978-3-8351-0179-1, Kapitel 8.