Homophone Verschlüsselung
Die homophone Verschlüsselung (von altgriechisch ὅμος hómos „gleich“ und φωνή phonḗ „Stimme“ = „gleich klingend“) ist eine bereits im 17. Jahrhundert weit verbreitete polyalphabetische[1] Verschlüsselungsmethode, bei der im Gegensatz zur einfachen monoalphabetischen Substitution die Klartextzeichen (zumeist: Buchstaben) auch durch mehrere (unterschiedliche) Geheimtextzeichen substituiert werden können.
Die wesentliche Schwäche der einfachen monoalphabetischen Substitution ist, dass jeder Klartextbuchstabe stets nur durch ein einziges Geheimtextzeichen verschlüsselt wird. Der so entstehende Geheimtext ist deshalb anfällig für statistische Angriffsmethoden. Beispielsweise genügt eine simple Häufigkeitszählung der Geheimtextzeichen, um den in den meisten Sprachen häufigsten Buchstaben E (Häufigkeit im Deutschen etwa 17,7 %) schnell zu identifizieren.
Diesem Angriff wirkt die homophone Verschlüsselung entgegen, indem sie mehrere Substitute für häufiger verwendete Buchstaben, wie zum Beispiel E oder N, erlaubt. Umgekehrt, aus Sicht des Geheimtextes formuliert, können unterschiedliche Geheimtextzeichen die Verschlüsselung desselben Klartextbuchstabens bedeuten (daher der Name homophon), was die unbefugte Entzifferung des Geheimtextes wesentlich erschwert. Die homophone Verschlüsselung stellt somit eine kryptographische Verbesserung der einfachen monoalphabetischen Substitutionsverfahren dar.
Beispiel
Wie bei allen monoalphabetischen Substitutionsverfahren, wird auch bei der homophonen Verschlüsselung nur ein einziges festes Substitutionsalphabet zur Ver- und Entschlüsselung verwendet. Um das Ziel, nämlich die Einebnung der unterschiedlichen Häufigkeiten der Klartextbuchstaben zu erreichen, kann man beispielsweise jedem Buchstaben des Alphabets so viele Geheimtextzeichen zuordnen wie seiner relativen Häufigkeit in Prozent entspricht, was ein Geheimtextalphabet von 100 Zeichen ergibt. Die typischen Häufigkeiten der Buchstaben in der deutschen Sprache sind in dem folgenden Diagramm dargestellt:
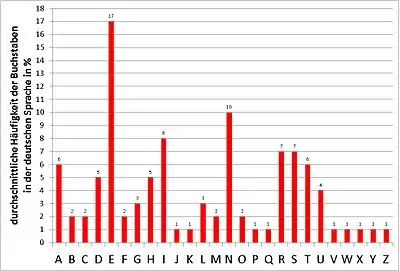
Bildet man nun die 26 Buchstaben des Alphabets auf 100 Geheimzeichen ab, im einfachsten Fall auf die Zahlen 00 bis 99, und zwar so, dass dem A sechs Geheimzeichen, dem B zwei, dem C zwei, dem D fünf zugeordnet werden, und so weiter, so tritt im Geheimtext jede (Geheim-)Zahl mit einer mittleren Häufigkeit von 1 % auf. Eine Häufigkeitsanalyse der Einzelzeichen ergibt nun keine Ansatzpunkte mehr für die Entzifferung.
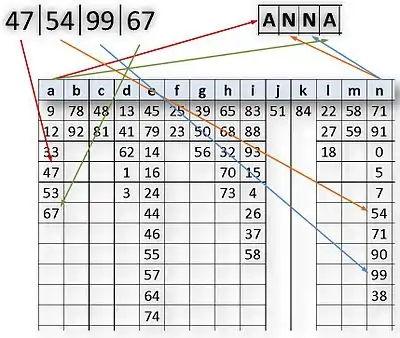
Um den Text dennoch zu knacken, muss der Angreifer nun raffiniertere Methoden anwenden. Hierzu kann er anstelle von einzelnen Zeichen (Monogrammen) die Analyse auf Bigramme (Zeichenpaare), Trigramme oder Tetragramme ausweiten. Mögliche Angriffspunkte sind charakteristische Bigramme wie CH, CK oder QU sowie die reversen EN und NE oder ER und RE. Hierzu benötigt er jedoch deutlich längere Texte. Hinreichend kurze, homophon verschlüsselte Texte (weniger als achtzig Buchstaben) sind gegen unbefugte Entzifferung recht gut geschützt.
Siehe auch
Literatur
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, ISBN 3-540-67931-6, S. 35 ff.
- Stephen Pincock, Mark Frary: Geheime Codes. Die berühmtesten Verschlüsselungstechniken und ihre Geschichte. Ehrenwirth in der Verlagsgruppe Lübbe, Bergisch Gladbach 2007, ISBN 978-3-431-03734-0, S. 32f.
- Simon Singh: Geheime Botschaften. Carl Hanser Verlag, München 2000, ISBN 3-446-19873-3, S. 74f.
Einzelnachweise
- Prof. Dr. Albrecht Beutelspacher: Geheimsprachen. 4. Auflage. Verlag C.H.Beck oHG, München, ISBN 3-406-49046-8, S. 29.