Caesar-Verschlüsselung
Die Caesar-Verschlüsselung (auch als Cäsar-Chiffre, Cäsar-Algorithmus, Caesar-Verschiebung, Verschiebechiffre oder als Einfacher Caesar bezeichnet) ist ein einfaches symmetrisches Verschlüsselungsverfahren, das auf der monographischen und monoalphabetischen Substitution basiert. Als eines der einfachsten und unsichersten Verfahren dient es heute hauptsächlich dazu, Grundprinzipien der Kryptologie anschaulich darzustellen. Der Einfachheit halber werden oftmals nur die 26 Buchstaben des lateinischen Alphabets ohne Unterscheidung von Groß- und Kleinbuchstaben als Alphabet für Klartext und Geheimtext verwendet und Sonderzeichen, Satzzeichen usw. nicht beachtet.
Algorithmus
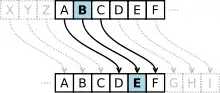
Bei der Verschlüsselung wird jeder Buchstabe des Klartexts auf einen Geheimtextbuchstaben abgebildet. Diese Abbildung ergibt sich, indem man die Zeichen eines geordneten Alphabets um eine bestimmte Anzahl zyklisch nach rechts verschiebt (rotiert); zyklisch bedeutet, dass man beim Verschieben über Z hinaus wieder bei A anfangend weiterzählt. Die Anzahl der verschobenen Zeichen bildet den Schlüssel, der für die gesamte Verschlüsselung unverändert bleibt. Beispiel für eine Verschiebung um drei Zeichen:
Klar: a b c d e f g h i j k l m n o p q r s t u v w x y z Geheim: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
Aus dem Klartext „caesar“ wird somit der Geheimtext „FDHVDU“. Für die Entschlüsselung wird das Alphabet um dieselbe Anzahl Zeichen nach links rotiert.
Mathematisch lässt sich die Caesar-Verschlüsselung mit Hilfe der Modulo-Addition beschreiben. Hierzu werden zunächst alle Zeichen des Alphabets auf einen Restklassenring abgebildet, zum Beispiel a=0, b=1, c=2, …, z=25. Die Verschlüsselung eines Klartextbuchstabens mit einer Verschiebung um Zeichen und einem Alphabet mit 26 Zeichen ist dann definiert als:
Entsprechend dazu lautet die Entschlüsselung eines Geheimtextbuchstabens :
Geschichte
Der Name der Caesar-Verschlüsselung leitet sich vom römischen Feldherrn Gaius Julius Caesar ab, der nach der Überlieferung des römischen Schriftstellers Sueton diese Art der geheimen Kommunikation für seine militärische Korrespondenz verwendet hat. Dabei benutzte Caesar eine Verschiebung des Alphabets um drei Buchstaben.
Sueton beschreibt das Verfahren wie folgt:
“[…] si qua occultius perferenda erant, per notas scripsit, id est sic structo litterarum ordine, ut nullum verbum effici posset: quae si quis investigare et persequi velit, quartam elementorum litteram, id est D pro A et perinde reliquas commutet.”
„[…] wenn etwas Geheimes zu überbringen war, schrieb er in Zeichen, das heißt, er ordnete die Buchstaben so, dass kein Wort gelesen werden konnte: Um diese zu lesen, tauscht man den vierten Buchstaben, also D für A aus und ebenso mit den restlichen.“[1]
Nach Sueton verwendete auch der römische Kaiser Augustus das Verfahren, jedoch mit einer Verschiebung um einen Buchstaben und ohne Rotation des Alphabets. Statt eines X, des letzten Buchstabens des damaligen lateinischen Alphabets, schrieb Augustus AA.
Leon Battista Alberti verbesserte das Verfahren im 15. Jahrhundert durch die Entwicklung der Chiffrierscheibe. Die Chiffrierscheibe erleichtert die Durchführung der Caesar-Verschlüsselung mit beliebigen Verschiebungen, indem die innere Scheibe um die Anzahl der verschobenen Buchstaben zur äußeren Scheibe gedreht wird und sich somit die ersetzten Buchstaben ablesen lassen. Darüber hinaus beschrieb Alberti auch die Verwendung der Chiffrierscheibe bzw. deren Varianten zur Durchführung von komplexeren monoalphabetischen und polyalphabetischen Substitutionsverfahren.
1508 beschrieb Trithemius ein polyalphabetisches Substitutionsverfahren mit Hilfe der von ihm erfundenen Tabula recta. Dieses Verfahren, welches im 16. Jahrhundert als Vigenère-Verschlüsselung bekannt wurde, basiert im Wesentlichen auf der Caesar-Verschlüsselung, allerdings pro Buchstabe abwechselnd mit einer anderen Verschiebung, was die Sicherheit erheblich erhöht.
Entzifferung und Sicherheit
Wie alle monoalphabetischen Verschlüsselungsverfahren bietet auch die Verschiebechiffre keine hinreichende Sicherheit gegen unbefugte Entzifferung und kann sehr leicht „geknackt“ werden. Die in der natürlichen Sprache ungleiche Verteilung der Buchstaben wird durch diese Art der Verschlüsselung nicht verborgen, so dass eine Häufigkeitsanalyse das Wirken einer einfachen monoalphabetischen Substitution enthüllt.
Das folgende Diagramm zeigt die Häufigkeitsverteilung der Buchstaben in einem längeren Text in deutscher Sprache:
Wie zu erwarten, ist der häufigste Buchstabe E, gefolgt von N und I, wie es im Deutschen üblicherweise der Fall ist. Wird der Text mit dem Schlüssel 10 (oder anders gesagt, mit dem Schlüsselbuchstaben J) chiffriert, erhält man einen Geheimtext, der folgende Häufigkeitsverteilung besitzt:
Der häufigste Buchstabe ist hier O, gefolgt von X und S. Man erkennt auf den ersten Blick die Verschiebung des deutschen „Häufigkeitsgebirges“ um zehn Stellen nach hinten und besitzt damit den Schlüssel. Voraussetzung ist lediglich, dass man die Verteilung der Zeichen des Urtextes vorhersagen kann.
Besitzt man diese Information nicht oder möchte man auf die Häufigkeitsanalyse verzichten, kann man auch die Tatsache ausnutzen, dass bei der Cäsar-Chiffre nur eine sehr kleine Anzahl möglicher Schlüssel in Frage kommt. Da die Größe des Schlüsselraums nur 25 beträgt, was einer „Schlüssellänge“ von nicht einmal 5 bit entspricht, liegt nach Ausprobieren spätestens nach dem 25. Versuch der Klartext vor. Eine erschöpfende Schlüsselsuche (Exhaustion) ist bei der Caesar-Verschlüsselung trivial realisierbar. Da dies auch ohne Computer oder Rechenmaschine mit geringem Aufwand möglich ist, bestand die Sicherheit der Caesar-Verschlüsselung schon zu ihren Anfängen nicht auf der Geheimhaltung des Schlüssels, sondern im Wesentlichen auf der Geheimhaltung des Verfahrens, und entspricht damit nicht dem im 19. Jahrhundert postulierten Prinzip von Auguste Kerckhoffs.
Schlüsselbuchstabe
Die Verschiebung des Alphabets um N Zeichen (N = 1…25) stellt den Schlüssel dar. Statt die Verschiebung als Zahl anzugeben, kann man sie auch als Schlüsselbuchstaben angeben. Hierbei gibt es zwei gängige Konventionen:
- A entspricht keiner Verschiebung, B einer Verschiebung um 1, C einer Verschiebung um 2 usw.
- A entspricht einer Verschiebung um 1, B einer Verschiebung um 2, C einer Verschiebung um 3 usw.
Die erste Konvention ergibt sich, wenn man den Schlüsselbuchstaben aus den beiden übereinander liegenden Alphabeten abliest („a“ auf „D“ ist eine Verschiebung um drei Zeichen). Dies ist auch bei der verwandten Vigenère-Verschlüsselung üblich. Zudem entspricht diese Konvention der Abbildung von Buchstabe auf Zahl, wie sie üblicherweise für die Modulo-Rechnung durchgeführt wird. Die zweite Konvention entspricht der natürlichen Nummerierung der Verschiebungen. Ein historischer Bezug, dass Caesar und Augustus jeweils ihren Anfangsbuchstaben als Schlüsselbuchstaben verwendeten, ist von Sueton nicht überliefert.
Da sich beide Konventionen widersprechen, ist die Angabe eines Schlüsselbuchstabens missverständlich, die Angabe als Zahl hingegen eindeutig.
Varianten
Heute ist die Caesar-Verschlüsselung als ROT13 mit einer Verschiebung um 13 Zeichen in Gebrauch, um Textinhalte wie Spoiler oder Pointen gegen unabsichtliches Lesen zu verschleiern. Da das heutige lateinische Alphabet aus 26 Zeichen besteht, wird durch die zyklische Verschiebung um 13 Zeichen zunächst der Text verschlüsselt und durch eine zweite Verschlüsselung mit demselben Schlüssel eine Gesamtverschiebung um 26 Zeichen erreicht und so der Originaltext zurückgewonnen. Dies ist ein besonders einfacher Fall einer involutorischen Verschlüsselung. Bei involutorischen Verfahren sind Verschlüsselung und Entschlüsselung identisch, und eine zweifache Anwendung des Verfahrens liefert den ursprünglichen Klartext wieder zurück.

Neben der Nutzung eines veränderten Alphabets, in dem etwa Ziffern und Sonderzeichen enthalten sind, gibt es zudem die Variante der umgekehrten oder revertierten Caesar-Verschlüsselung. Hierbei wird die Reihenfolge des Geheimalphabets umgekehrt und eine Verschiebung durchgeführt. Bei einer Verschiebung um vier Zeichen ergibt sich dann das folgende Alphabet:
Klar: a b c d e f g h i j k l m n o p q r s t u v w x y z Geheim: D C B A Z Y X W V U T S R Q P O N M L K J I H G F E
In diesem Fall würde aus „caesar“ der Geheimtext „BDZLDM“ entstehen. Eine weitere Variante entsteht, wenn man bei der revertierten Caesar-Verschlüsselung die Verschiebung weglässt und sich somit das folgende Alphabet ergibt:
Klar: a b c d e f g h i j k l m n o p q r s t u v w x y z Geheim: Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
Diese Variante ist unter Anwendung des hebräischen Alphabetes als Atbasch bekannt.
Literatur
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, ISBN 3-540-67931-6.
- Rudolf Kippenhahn: Verschlüsselte Botschaften. Die Geheimschrift des Julius Cäsar – Geheimschriften im I. und II. Weltkrieg – Das Codebuch des Papstes – Enigma. 4. Auflage. Nikol, Hamburg 2006, ISBN 3-937872-37-X.
Weblinks
- Tool zum Ausprobieren der Caesarchiffren
- Tool zur Verschlüsselung mit Cäsar-Chiffre, Affine Chiffre und ROT13
- Tool für Brute-Force Angriffe bei Cäsar-Chiffren bzw. zum "Brechen" dieser
- Website zur Online-Verschlüsselung (ROT1 bis ROT25)
- Video: Cäsar-Verschlüsselung. Christian Spannagel 2012, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/19812.
- Eine in C geschriebene Version des Cäsar Algorithmus.