Poincaré-Kugel
Die Poincaré-Kugel ist ein Werkzeug zur Darstellung der Polarisationszustände elektromagnetischer Wellen wie zum Beispiel Licht. Jeder Polarisationszustand entspricht einem Punkt auf der Kugel, wobei sich vollständig polarisierte Zustände auf der Oberfläche, teilpolarisierte Zustände innerhalb der Kugel und der unpolarisierte Zustand im Zentrum befinden. Lineare Polarisationen befinden sich am Äquator der Kugel, zirkulare Polarisationen an den Polen und elliptische Polarisationen dazwischen. Orthogonale Polarisationen befinden sich auf der Kugeloberfläche einander gegenüber. Die Poincaré-Kugel ist benannt nach dem Physiker Henri Poincaré.
Mathematische Beschreibung
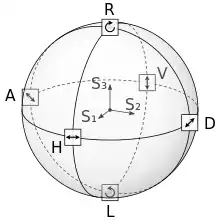
Polarisationszustände elektromagnetischer Wellen lassen sich unter anderem mit Hilfe normierter Stokes-Parameter beschreiben, wo zur vollständigen Festlegung die drei Parameter S1, S2 und S3 benötigt werden. Diese Parameter spannen einen dreidimensionalen Vektorraum auf, in dem sich die Polarisationszustände als Punkte befinden. Die Stokes-Vektoren aller physikalisch möglichen Polarisationen befinden sich dann innerhalb einer Einheitskugel, der Poincaré-Kugel.[1]
Auf den Schnittpunkten der Koordinatenachsen mit der Kugeloberflächen befinden sich folgende Polarisationen:
- H: linear horizontal polarisiert
- V: linear vertikal polarisiert
- D: linear diagonal polarisiert (manchmal auch „/“ oder P für plus)
- A: linear antidiagonal polarisiert (manchmal auch „\“ oder M für minus)
- R: rechtshändig zirkular polarisiert (manchmal auch RHCP)
- L: linkshändig zirkular polarisiert (manchmal auch LHCP)
Den Punkten der Kugeloberfläche entsprechen die reinen Polarisationszustände, dem Innern die gemischten Polarisationen. Nach innen nimmt die Reinheit kontinuierlich ab bis zum unpolarisierten Zustand im Mittelpunkt.
Anwendung
Die Poincaré-Kugel eignet sich zur intuitiven Veranschaulichung von Polarisationszuständen und insbesondere von Transformationen zwischen verschiedenen Polarisationen. Ähnliche Polarisationszustände sind stets benachbart und kontinuierliche Transformationen wie zum Beispiel beim Durchgang einer Welle durch ein doppelbrechendes Medium entsprechen kontinuierlichen Verschiebungen auf der Kugel. Lineare Transformationen der Polarisation entsprechen einer Drehung auf der Poincaré-Kugel um eine feste Drehachse.[2] Beispiele:
- Eine Lambda/2-Platte dreht die Poincaré-Kugel um 180°. Die Drehachse liegt auf dem Äquator und ist entsprechend der Orientierung der Wellenplatte ausgerichtet.
- Eine Lambda/4-Platte dreht die Poincaré-Kugel um 90°. Die Drehachse liegt auf dem Äquator und ist entsprechend der Orientierung der Wellenplatte ausgerichtet.
- Ein elektrooptischer Modulator dreht die Poincaré-Kugel um einen variierbaren Winkel. Die Drehachse liegt auf dem Äquator und ist entsprechend der Orientierung des elektrooptischen Modulators ausgerichtet.
Beziehung zu anderen Darstellungen
Die Poincaré-Kugel ist mathematisch äquivalent zur Bloch-Kugel, die den Hilbert-Raum der möglichen Zustände eines quantenmechanischen Zweizustandssystems (Qubit) veranschaulicht. Die Orientierung mit der die beiden Kugeln aufeinander abgebildet werden können, hängt hierbei davon ab, welche beiden orthogonalen (gegenüberliegenden) Polarisationen als Basiszustände ausgewählt werden. Diese Abbildung entspricht der Verwendung der Polarisation eines Photons als Qubit.
Wird die Polarisation anstelle von Stokes-Parametern mathematisch äquivalent mit Jones-Vektoren beschrieben, so entspricht der Jones-Vektor gerade dem Bloch-Vektor sofern als Basiszustände auf der Poincaré-Kugel die Polarisationen H und V ausgewählt werden.
Überträgt man Punkte der Poincaré-Kugel auf die Riemannschen Zahlenkugel, dann erhält man eine komplexe Zahl, die die Amplituden- und Phasenbeziehung von horizontaler und vertikaler Schwingung beschreibt.
Einzelnachweise
- Dieter Meschede: Optik, Licht und Laser. Wiesbaden 2005, ISBN 978-3-8351-0143-2, S. 62.
- Georg A. Reider: Photonik: Eine Einführung in die Grundlagen. Wien 2012, ISBN 978-3-7091-1520-6, S. 32.