Pathfinding
Pathfinding bzw. Wegfindung ist in der Informatik die algorithmengestützte Suche nach dem oder den optimalen Wegen (englisch path – Pfad) von einem gegebenen Startpunkt zu einem oder mehreren Zielpunkten. Die Einsatzgebiete reichen von Netzwerk-Flussanalyse über Routenplanung bis zu Computerspielen.
Aufgabenspektrum
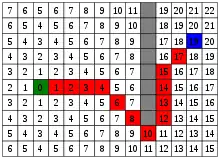
rot: Weg
blau: Zielfeld
grau: Hindernis
In vielen, aber nicht notwendigerweise in allen Fällen ist die Suche nach dem optimalen Weg zwischen zwei Punkten auch die Suche nach der kostengünstigsten oder kürzesten Route mit den wenigsten Hindernissen. Dabei handelt es sich zwar um das „klassische Lernbeispiel“, aber die richtige Antwort auf ein Pathfinding-Problem ist in der Praxis nur selten auch wirklich die Luftlinie zwischen einem gegebenen Start- und einem gegebenen Zielpunkt. Die Suche wird häufig durch andere Faktoren mitbestimmt, die den Begriff des Optimums verzerren und dadurch andere Routen sinnvoller erscheinen lassen, wie z. B.:
- nicht oder nur bedingt passierbare Hindernisse, die den direkten Weg versperren
- variable Kosten in der Fortbewegung, z. B. für erhöhten Energieverbrauch gegen Strömung
- mehrdimensionale Kostenmodelle in der Fortbewegung, z. B. Zeit vs. Energie vs. Gefahren
- die Rasterung bzw. Diskretisierung der Umwelt, ähnlich einem Schach- oder Spielfeld
- die Notwendigkeit, auf der Route bestimmte Zwischenpunkte zu passieren oder günstige Abbruchmöglichkeiten für die Route offenzulassen
- nichtkartesische Koordinaten
Algorithmen
Um den Anforderungen an Pathfinding je nach Kontext zu entsprechen, wurde in der Vergangenheit eine Vielzahl von Algorithmen entwickelt, von denen fast alle ihre speziellen Vor- und Nachteile haben.
Eine weit verbreitete Pathfinding-Methode ist der A*-Algorithmus, bei dem die Umgebung als Karte als Graph interpretiert wird und zur Berechnung Heuristiken verwendet werden. Zuerst müssen Start- und Zielknoten festgelegt werden. Danach erhält jedes Feld vom Startpunkt aus einen Wert, der proportional zur Entfernung ansteigt. Der optimale Weg ist derjenige, bei dem das Zielfeld den geringsten Wert erhält. Hindernisse, die zwar zu bewältigen sind, aber einen Zeitverlust aufbringen, können dadurch leicht berücksichtigt werden. (Ein Beispiel dafür wäre ein Sumpf, bei dem der Wert pro Feld beispielsweise 2 statt 1 ansteigt und deshalb möglicherweise ein schnellerer, aber längerer Weg außen herum existiert.)
Hat man keine Heuristik, um die Kosten zwischen Knoten abzuschätzen, kann man statt des A*-Algorithmus den Algorithmus von Dijkstra verwenden. Um alle kürzesten Pfade von einem Knoten zu allen anderen Knoten auch in einem Graphen mit negativen Kantengewichten berechnen zu können, kann der Bellman-Ford-Algorithmus verwendet werden. Sucht man nicht nur die günstigsten Pfade eines Knotens zu allen anderen Knoten im Graph, sondern die günstigsten Pfade zwischen allen Knotenpaaren, so kann man den Min-Plus-Matrixmultiplikations-Algorithmus oder den Algorithmus von Floyd und Warshall verwenden.
Anwendungsbeispiele
Im Computerspiele-Bereich reicht die Historie des Pathfindings von Spiele-Klassikern wie Pac-Man bis in die Gegenwart. Während bei Pac-Man z. B. einfache Pathfinding-Algorithmen dafür sorgten, dass sich Gespenster als Computergegner durch ein virtuelles Labyrinth bewegten, dienen sie heute in Echtzeit-Strategiespielen der Routenplanung ganzer Militärverbände und in Ego-Shootern der ausgefeilten Orientierung computergesteuerter Bot-Gegner. Echtzeit-Strategiespiele basieren in der Regel auf zweidimensionalen Karten, die in einzelne Kacheln unterteilt sind. Besondere Schwierigkeiten ergeben sich z. B. bei Wegen, die dynamisch versperrt werden, etwa wenn mehrere Einheiten gleichzeitig eine enge Passage durchqueren. In Ego-Shootern, bei deren Karten die dritte Dimension eine wichtigere Rolle spielt, wird häufig mit Wegpunkten gearbeitet, an denen sich die Künstliche Intelligenz orientiert. Fast immer ist „gutes“ Pathfinding auch mit hoher Komplexität verbunden. Im Computerspiel Age of Empires II z. B. nahm allein das Pathfinding auf damals handelsüblicher Hardware 60 bis 70 Prozent der gesamten CPU-Leistung während des Spielens in Anspruch.[1]
Entsprechend große Anstrengungen werden unternommen, um Pathfinding-Algorithmen zu optimieren. Die Lösungskonzepte reichen von Vorberechnungen (d. h. Reduzierung der Laufzeit auf Kosten von Speicherbedarf) bis hin zu vorteilhaften Annahmen, die ein Programm bzgl. seines konkreten Anwendungsfalls bereits im Vorfeld treffen kann (z. B. „zwischen A und B liegt eine unüberwindbare Schlucht, über die nur eine einzige Brücke führt, also wird die Route zwangsläufig dort entlang führen und nicht woanders“).[2]
Verschiedene Algorithmen sind in der freien Python-Bibliothek NetworkX implementiert.[3]
Siehe auch
Einzelnachweise
- Gamasutra, Dave C. Pottinger, 2000: „Terrain Analysis in Realtime Strategy Games“ (Memento vom 21. Dezember 2008 im Internet Archive) (MS Word; 980 kB)
- http://3dpathfinding.homeunix.org/ (Memento vom 7. Juni 2007 im Internet Archive) Technische Universität München, Daniel Kastenholz, 2006: „3D Pathfinding“
- Algorithms - Shortest Paths. In: NetworkX 2.2 documentation. Abgerufen am 24. Oktober 2018 (englisch).