Optisches Gitter (Quantenoptik)
Ein optisches Gitter (englischer Fachbegriff optical lattice) bezeichnet in der Quantenoptik eine räumlich periodische Struktur aus Laserstrahlung, in der Atome oder Moleküle gefangen werden können.
Funktionsweise
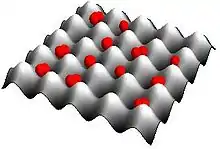
Die Struktur des optischen Gitters entsteht durch die Interferenz von Laserlicht. Dabei kommt es bei geeigneter Wahl der Laserparameter zu einer stehenden Welle, die aufgrund der Stark-Verschiebung für Atome ein periodisches Potential hervorruft. Das zugrundeliegende Prinzip ist mit dem der optischen Pinzette identisch: das Laserlicht induziert in jedem der Atome ein elektrisches Dipolmoment, dessen Wechselwirkung mit dem Licht in einer Kraft auf das Atom resultiert. Je nach Vorzeichen der Verstimmung des Laserlichts bezüglich der atomaren Übergangsfrequenz werden die Atome in die Knoten (Intensitätsminima) bzw. Bäuche (Intensitätsmaxima) der stehenden Welle gezogen. Die genaue Geometrie des erzeugten Potentials hängt von der Anordnung der Laserstrahlen und der daraus resultierenden Komplexität des Interferenzmusters ab.
Bandstruktur
Das periodische Potential verändert die Dispersionsrelation für die Bewegung der Atome entsprechend dem Bloch-Theorem. Es entsteht eine Bandstruktur analog zur Bandstruktur der Elektronen in Kristallen. Mit der Geometrie des Interferenzmusters lässt sich im Prinzip auch diese Bandstruktur maßschneidern. Im Gegensatz zu Festkörpersystemen ist es in optischen Gittern zusätzlich möglich, die Potentialtiefe und damit die Bandstruktur dynamisch (also während die Atome darin sitzen) zu verändern.
Konsequenzen
Wenn es eine hinreichend starke Wechselwirkung zwischen den Atomen gibt, erlaubt die Bandstruktur die Bildung von dunklen (lochartigen) und hellen (teilchenartigen) Solitonen, da die Wechselwirkung unter Umständen genau die Dispersion kompensieren kann. Auf eine externe Kraft, z. B. die Gravitation, reagieren die Atome im optischen Gitter mit Bloch-Oszillationen, die sich in diesen Systemen extrem genau vermessen lassen.
Beobachtung
Meistens werden die Atome nicht im optischen Gitter beobachtet, sondern nach Abschalten des Lichtpotentials und einer gewissen Flugzeit. Dabei wird die Absorption eines Laserstrahls, der die Atome beleuchtet, auf einer CCD-Kamera registriert. Die Methodik ist vergleichbar mit der Detektion von Bose-Einstein-Kondensaten. Auf diese Weise kann man im Allgemeinen die Quasiimpuls-Verteilung messen, nicht jedoch direkt die räumliche Verteilung der Atome.
Insbesondere ist es schwierig, individuelle Gitterplätze zu beobachten, da diese im Extremfall nur eine halbe Lichtwellenlänge voneinander entfernt sind. Man hat daher bei optischer Beobachtung einzelner Gitterplätze mit der Beugungsbegrenzung der optischen Auflösung zu kämpfen. 2008 ist es jedoch mehreren Forschergruppen gelungen, einzelne Gitterplätze in einem optischen Gitter abzubilden, und – teilweise in Echtzeit und mit einer Detektionsempfindlichkeit, die dazu ausreicht, einzelne Atome nachzuweisen – deren Bewegung zu verfolgen. Darüber hinaus ist auch eine Methode entwickelt worden, die mit der Rasterelektronenmikroskopie verwandt ist und einzelne Atome durch Ionisation mit einem Elektronenstrahl nachweist, welcher sich wesentlich schärfer fokussieren lässt.[1]
Anwendung
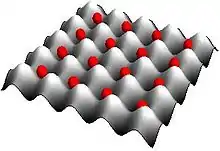
Werden die Senken eines dreidimensionalen optischen Gitters mit jeweils einem Atom gefüllt, so hat es viele Eigenschaften von Kristallen. Solche optischen Gitter haben gegenüber den aus der Festkörperphysik bekannten Systemen den Vorteil, dass sich ihre Parameter durch das verwendete Laserlicht leicht verändern lassen. Sie können daher als Modellsysteme für Probleme aus der Festkörperphysik verwendet werden und gelten als aussichtsreiche Kandidaten für die Realisierung eines Quantencomputers.
Atome in optischen Gittern gelten darüber hinaus neben gefangenen Ionen als aussichtsreiche Kandidaten für die Realisierung noch präziserer Atomuhren, so genannter Gitteruhren.
Einzelnachweise
- T. Gericke et al.: High-resolution scanning electron microscopy of an ultracold quantum gas. In: Nature physics. 2008, doi:10.1038/nphys1102 (Uni Ulm [PDF; 669 kB]).
Literatur
- Oliver Morsch, Markus Oberthaler: Dynamics of Bose-Einstein condensates in optical lattices. In: Reviews of Modern Physics. Band 78, Nr. 1, 27. Februar 2006, S. 179–215, doi:10.1103/RevModPhys.78.179 (englisch).
- Immanuel Bloch: Ultracold quantum gases in optical lattices. In: Nature Physics. Band 1, Nr. 1, 2005, S. 23–30, doi:10.1038/nphys138 (englisch).
- H.-J. Briegel, T. Calarco, D. Jaksch, J. I. Cirac, P. Zoller: Quantum computing with neutral atoms. In: Journal of Modern Optics. Band 47, Nr. 2–3, 2000, S. 415–451, doi:10.1080/09500340008244052, arxiv:quant-ph/9904010 (englisch).
Weblinks
- Einführung in optische Gitter
- Optische Gitter in der Quanteninformation
- Gitteruhr-Projekt der PTB
- Optische Detektion und Manipulation einzelner Atome
- A Quantum gas microscope for detecting individual atoms in a Bose-Hubbard optical lattice. (Nicht mehr online verfügbar.) Greiner Lab, Harvard, archiviert vom Original am 3. März 2015 (Beobachtung von ultrakalten Atomen in einem optischen Gitter in Echtzeit).