NARCH-Modell

Das NARCH-Modell (NARCH, Akronym für: Nonparametric AutoRegressive Conditional Heteroscedasticity, deutsch nichtparametrische autoregressive bedingte Heteroskedastizität) bzw. nichtparametrisches autoregressives Modell mit bedingter Heteroskedastizität ist ein stochastisches Modell zur Zeitreihenanalyse. Verwandt ist dieses Modell mit den parametrischen ARCH- beziehungsweise GARCH-Modellen (General AutoRegressive Conditional Heteroscedasticity). Anders als für ein parametrisches Modell wird in diesem nichtparametrischen Modell keine Anforderung an die Struktur der zugrundeliegenden Gesetzmäßigkeit gestellt.

Definition

Gegeben sei eine reellwertige Zeitreihe $\{S_{t}\}_{t\in \mathbb {Z} }$ . Das Modell

{\begin{aligned}S_{t}=\mu (S_{t-1},\dotsc ,S_{t-p})+\sigma (S_{t-1},\dotsc ,S_{t-q})\epsilon _{t}\end{aligned}}

heißt NARCH(p,q)-Modell. Dabei bezeichnet $\mu$ die Trendfunktion, $\sigma$ die Volatilitätsfunktion und $\epsilon _{t}$ den Rauschterm, der aus einer Folge $\{\epsilon _{t}\}_{t\in \mathbb {Z} }$ unabhängig und identisch verteilter Zufallsvariablen (englisch independent identical distributed, iid) mit Median Null und Varianz Eins (iid(0,1)) besteht. Die Modellparameter $p$ sowie $q$ sind positive ganze Zahlen.

An die Trend- und die Volatilitätsfunktion werden keine expliziten Anforderungen gestellt, sie sollen lediglich hinreichend glatte Funktionen darstellen. Das NARCH-Modell wird aufgrund seiner Berechnungskomplexität und Anforderungen an die Menge der vorliegenden Daten in dieser ursprünglichen Form selten angewendet.

Erweiterungen

S-NARCH

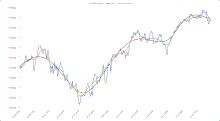
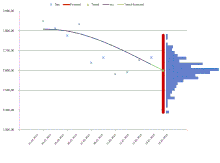
Beispiel einer S-NARCH-Modell-Analyse: 250-Tage-Ausschnitt der DAX-Schlusskurse zusammen mit der durch das S-NARCH-Modell geschätzten Sekundär- und der Tertiärtrendfunktion.

Beispiel einer S-NARCH-Modell-Prognose: S-NARCH-Prognose bezüglich Trend und Volatilität zusammen mit dem Konfidenzintervall der Prognose sowie der empirischen Dichte der Rauschverteilung.

Ein spezielles NARCH-Modell stellt das S-NARCH-Modell (Akronym für Signbased NARCH) dar.[1] Für finanzmathematische Zeitreihen, wie sie beispielsweise an der Börse in Form von Aktienkursen und Indizes vorkommen, kann mit Hilfe der technischen Analyse ein spezielles nichtparametrisches ARCH-Modell definiert werden. Hierbei wird die Trenddefinition aus der technischen Analyse auf die Beschaffenheit der Trendfunktion des NARCH-Modells bezogen. Weiterhin fließen Definitionen aus der robusten Regression ein, indem ausschließlich die Folge der Residuenvorzeichen $\{\operatorname {Sign} ({\hat {\mu }}_{t}-S_{t})\}_{t\in \mathbb {Z} }$ bezüglich der geschätzten Trendfunktion ${\hat {\mu }}$ betrachtet werden. Gleiche aufeinanderfolgende Vorzeichen (sogenannte Runs) dürfen wie in der technischen Analyse gewisse Schwellwerte nicht überschreiten (statistische Signifikanz). Unterschieden wird in kurz-, mittel- und langfristigen Trends, wobei die aus der technischen Analyse abgeleiteten maximalen Runlängen in den Vorzeichenfolgen hierbei etwa 5, 15 und 28 respektive entsprechen. Mit Hilfe dieser Modellbeschreibung lässt sich sowohl Trend als auch Volatilität und Wahrscheinlichkeitsverteilung des Rauschterms aus den Daten schätzen. Die Modellparameter $p$ und $q$ sind lediglich interne und implizite Parameter. Die aus dem Modell resultierenden Funktionsschätzer ${\hat {\mu }}$ und ${\hat {\sigma }}$ für den Trend und die Volatilität bestehen aus Splines, somit können durch Spline-Extrapolation einfach Prognosen erstellt werden. Das Ergebnis ist dann neben der Kursprognose auch ein Konfidenzintervall für ebendiese Kursprognose.

Eine spezielle Eigenschaft dieses Modells ist, dass weder für die Definition noch für die Berechnungen Verteilungsannahmen getroffen werden müssen.

Literatur

Jianqing Fan, Qiwei Yao: Nonlinear Time Series. Springer, 2005
John J. Murphy: Technische Analyse der Finanzmärkte. Finanz Buch Verlag, 2003

Referenzen

Lars Metzner: Ein vorzeichenbasiertes NARCH-Modell für finanzmathematische Zeitreihen. Masterarbeit in Aktuarwissenschaften, Universität Ulm, 2018

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Lars Metzner: Ein vorzeichenbasiertes NARCH-Modell für finanzmathematische Zeitreihen. Masterarbeit in Aktuarwissenschaften, Universität Ulm, 2018