Multiplizierer (Digitaltechnik)

Ein Multiplizierer ist in der Digitaltechnik eine elektrische Schaltung, die aus zwei oder mehr digitalen Zahlen mit der mathematischen Operation der Multiplikation das Produkt ermittelt. Der Multiplizierer ist bei Prozessoren Teil der arithmetisch-logischen Einheit (ALU) und kommt dort als Multiplikationsakkumulator (MAC) vor, kann aber in programmierbaren digitalen Schaltungen wie FPGAs auch als eine eigenständige Funktionseinheit realisiert werden.

Neben der Addition, welche in digitalen Schaltungen mit geringerem schaltungstechnischem Aufwand in Form von Addierwerken realisiert ist, ist eine schnelle, hardwarebasierende Multiplikation insbesondere im Bereich der digitalen Signalverarbeitung wesentlich. Anwendungsgebiete des Multiplizierers liegen daher bei der Signalverarbeitung wie der Bildverarbeitung oder im Bereich digitaler Filter. Er findet aber auch Anwendung in der digitalen Regelungstechnik. Einer der ersten Einsatzbereiche waren digitale Signalprozessoren (DSP).

Arten

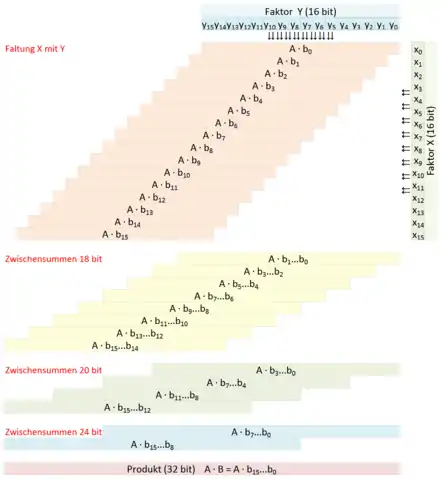
Multiplizierer 16x16=32 bit

Multiplizierer werden aufgrund der verarbeiteten Zahlenformate unterschieden:

Festkomma-Multiplizierer multiplizieren Festkommazahlen.
Gleitkomma-Multiplizierer multiplizieren Gleitkommazahlen.

Der Aufwand ist im Wesentlichen durch die Anzahl der zu multiplizierenden Bits (steigt quadratisch) bestimmt. Gleitkomma-Multiplizieren benötigen noch etwas zusätzliche Logik:

Einen Addierer für die Exponenten, der parallel arbeiten kann
Ein XOR-Gatter für das Vorzeichen
Behandlung des Verlusts des MSB (höchste Bit, most significant bit) nach der Multiplikation: Dekrement und Verschiebung.
Behandlung für NANs und INFs am Eingang bzw. bei Überlauf- und Unterlauf.

Bei Verwendung von parallelen Multiplizieren in modernen CPUs und Grafikkarten liegt der Hauptaufwand (double: ca. 97 Prozent, float: ca. 92 Prozent) im Multipliziernetzwerk.

Festkommamultiplizierer

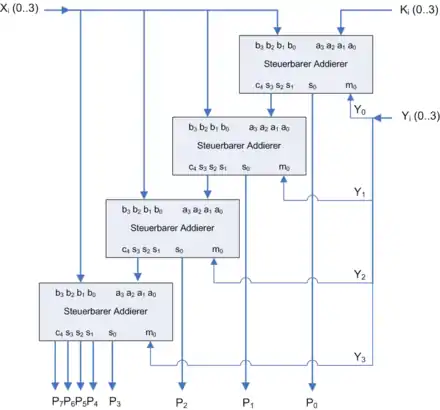
Paralleler Multiplizierer für 4 Bit.

s_{i}

= Summanden

c_{i}

= Carry-Output

m_{0}

= Input Enable

b_{i}

Die binäre Multiplikation verläuft analog wie im dezimalen System, und kann in digitalen Schaltungen als eine Abfolge von Additionen und Schieboperationen realisiert werden. In nebenstehender Schaltung ist ein vorzeichenloser, paralleler Multiplizierer (MAC) für zwei je vier Bit breite Zahlen X und Y und dem Summanden K mit Volladdierern dargestellt. Die acht Ausgabebits P werden in der kombinatorischen Logik mit folgender Gleichung gebildet:

P=X\cdot Y+K

Der Vorgang der Multiplikation gestaltet sich dabei nach folgendem Schema, die vier Eingangsbits K sind der Einfachheit wegen auf 0 gesetzt:

      1011   (X, entspricht dezimal der Zahl 11)
    · 1110   (Y, entspricht dezimal der Zahl 14)
    ------
 +    0000   (1011 · 0)
 +   1011    (1011 · 1, um eine Stelle nach links verschoben)
 +  1011     (1011 · 1, um zwei Stellen nach links verschoben)
 + 1011      (1011 · 1, um drei Stellen nach links verschoben)
 ---------
  10011010   (P, entspricht dezimal 154)

Dieser einfache Multiplizierer lässt sich aus einzelnen Volladdierern und die Schiebeoperation durch direkte Verschaltung realisieren. Die binären Stellen des Produktes P sind gleich der Summe der Stellen der beiden Faktoren X und Y. Ein in der Position fixer Kommapunkt wird generell nicht schaltungstechnisch abgebildet, sondern die Position des Kommapunktes im Produkt ergibt sich aus der Summe der Stellen nach dem Komma der beiden Eingangsfaktoren. Im obigen Beispiel ist bei beiden Faktoren die Stellenanzahl hinter dem Komma null, wodurch auch im Produkt der Kommapunkt rechts der letzten Stelle zu liegen kommt.

Bei vorzeichenbehafteten Zahlen, welche in digitalen Schaltungen meistens als Zweierkomplement dargestellt sind, ist eine entsprechende schaltungstechnische Erweiterung des Multiplizierers nötig. Die vorzeichenrichtige Multiplikation von zwei je vierstelligen binären Zahlen gestaltet sich nach folgendem Schema, wobei zu beachten ist, dass die letzte Zeile aufgrund des negativen Faktors subtrahiert werden muss:

       1001   (entspricht dezimal der Zahl -7)
     · 1101   (entspricht dezimal der Zahl -3)
     ------
 + 11111001   (1001 · 1, mit Vorzeichenerweiterung)
 + 0000000    (1001 · 0, um eine Stelle nach links verschoben und mit Vorzeichenerweiterung)
 + 111001     (1001 · 1, um zwei Stellen nach links verschoben und mit Vorzeichenerweiterung)
 - 11001      (1001 · 1, um drei Stellen nach links verschoben und mit Vorzeichenerweiterung)
 ----------
   00010101   (entspricht dezimal +21)

Schaltungstechnisch kann die Subtraktion in der letzten Zeile durch erweiterte Volladdierer realisiert werden, welche neben der Addition auch die Subtraktion beherrschen.

Der Parallelmultiplizierer, bei dem die Rechengeschwindigkeit nur von der maximalen Gatterlaufzeit abhängt, ist allerdings für größere Bitbreiten aufwendig zu realisieren. Ein anderes Verfahren ist der serielle Multiplizierer, bei welchem zu Lasten des Durchsatzes mit geringerem Hardwareaufwand pro Takt ein Bit (eine Stelle) des Ergebnisses berechnet wird. Des Weiteren existieren Verfahren, welche auf Tabellen mit bereits vorab berechneten Werten (engl. Look-Up-Tables) basieren. Es existieren auch effiziente Algorithmen, mit denen sich schnelle Multiplizierer mit moderatem schaltungstechnischen Aufwand realisieren lassen. Beispiele hierfür sind der Dadda-Tree-Multiplizierer, der Wallace-Tree-Multiplizierer und der Booth-Algorithmus.

Gleitkommamultiplizierer

Eine beliebige Gleitkommazahl x wird aus dem Vorzeichenbit s (±1), der Mantisse m und einem Exponenten e, mit einer willkürlich gewählten und fixen Basis b, gebildet:

x=s\cdot m\cdot b^{e}

Bei der in der Computertechnik üblichen Norm IEEE 754 zur Darstellung von Gleitkommazahlen wird mit einer Basis b = 2 und je nach benötigter Auflösung verschieden breiten Mantissen und Exponenten gearbeitet.

Die Multiplikation zweier Gleitkommazahlen lässt sich immer auf eine Multiplikation der beiden Mantissen und eine Addition der beiden Exponenten mit Festkommaarithmetik zurückführen. Die Addition und Multiplikation kann aus Geschwindigkeitsgründen parallel mit getrennten Schaltungsteilen erfolgen. Die einzelnen Schritte

Aufspalten der Faktoren in Vorzeichen, Exponenten und Mantissen. Die führende 1 bei normalisierten Mantissen (Exponent > 1) und die führende Null bei denormalisierter Mantisse (Mantisse = 0) sind hinzuzufügen.

Die folgenden Schritte können parallel ausgeführt werden:

Multiplikation der Mantissen: M = M₁ × M₂
Addition der Exponenten: E = E₁ + E₂ − Bias
Xor-Verknüpfung der Vorzeichen: S = S₁ + S₂

Nun folgt:

Bestimmung des MSBs, die 0 sind. Im Fall von normalisierten Faktoren kann dies 0 oder 1 sein, im Fall von denormalisierten Faktoren sind größerer Zahlen möglich (double bis 106): L

Fallunterscheidung:

Falls E − L ≤ −24 bzw. −53, ist das Ergebnis Null. Das Vorzeichen bleibt aber erhalten.
Falls E − L ≤ 0 ist, ist das Ergebnis eine denormalisierte Zahl.
Falls 0 < E − L < MaxBias ist, ist das Ergebnis eine normalisierte Zahl.
Falls MaxBias ≤ E − L ist, ist das Ergebnis unendlich.

Zusätzlich existieren bei Gleitkommamultiplizierern noch Steuerlogiken, welche das korrekte Vorzeichen des Ergebnisses bilden und bestimmte Sonderfälle des IEEE-754-Gleitkommaformates, wie „Keine Zahl“ (NaN, engl. für Not-A-Number), behandeln.

Hardwarerealisierung und zeitliches Verhalten

Alle Logikbauelemente besitzen eine Signallaufzeit. Mit zunehmender Bitbreite des Multiplizierers nimmt die Anzahl der Logikbauelemente, die parallel und/oder in Reihe geschaltet sind, zu. Mit zunehmender Anzahl von Logikbauelementen steigt die gesamte Signallaufzeit des Multiplizierers.

Literatur

Jean-Michel Muller: Elementary functions - Algorithms and Implementation. 2. Auflage. Birkhäuser, Lyon 2006, ISBN 0-8176-4372-9.

Weblinks

Multiplication in FPGAs (Memento vom 23. Oktober 2014 im Internet Archive) Schaltungstechnische Varianten, auf Englisch.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.