Beschleunigungspol

Der Beschleunigungspol (Formelzeichen P) ist bei einer ebenen Starrkörperbewegung derjenige Punkt in der Ebene, in dem ein dort befindliches Partikel des Starrkörpers keine Beschleunigung hat.[1] Der Beschleunigungspol liegt bei einer Bewegung in der xy-Ebene und Drehung um die z-Achse im Punkt

{\begin{pmatrix}p_{x}\\p_{y}\end{pmatrix}}={\begin{pmatrix}s_{x}+{\frac {\omega ^{2}{\ddot {s}}_{x}-{\dot {\omega }}{\ddot {s}}_{y}}{\omega ^{4}+{\dot {\omega }}^{2}}}\\s_{y}+{\frac {\omega ^{2}{\ddot {s}}_{y}+{\dot {\omega }}{\ddot {s}}_{x}}{\omega ^{4}+{\dot {\omega }}^{2}}}\end{pmatrix}}

Starrkörper (gelb) mit Bezugspunkt s, Beschleunigungspol p und Beschleunigungen (rot)

Die Indizes x und y verweisen auf die Raumrichtung, s ist der Bezugspunkt um den sich der Starrkörper dreht, ${\ddot {s}}$ die Beschleunigung des Bezugspunktes und $\omega ,{\dot {\omega }}$ sind die Drehgeschwindigkeit und -beschleunigung des Starrkörpers.

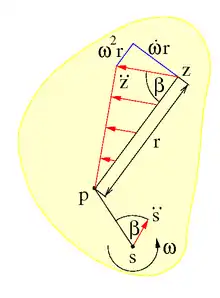
Sei der „Polabstand“ der Abstand r eines Partikels im Punkt z vom Beschleunigungspol p (siehe Bild). Dann gilt:

Wenn der Bezugspunkt nicht beschleunigt wird, dann liegt der Beschleunigungspol im Bezugspunkt.
Die Beschleunigung des Partikels wächst linear mit seinem Polabstand. Auf Kreisen um den Beschleunigungspol ist die Beschleunigung konstant.
Alle Partikel werden bei rotierendem Starrkörper in Richtung des Beschleunigungspols beschleunigt, quer dazu nur im Fall einer Winkelbeschleunigung des Starrkörpers.
Der Winkel β zwischen der Beschleunigungsrichtung des Partikels und der Richtung zum Beschleunigungspol ist für alle Partikel im Starrkörper gleich und höchstens 90°. Die Partikel werden niemals vom Beschleunigungspol radial weg getrieben.
Der Beschleunigungspol ist der Schnittpunkt zweier Radien, die unter dem Winkel β zu zwei gegebenen Beschleunigungsvektoren stehen.[1]
Die Beschleunigung eines Partikels in Richtung des Beschleunigungspols nimmt proportional zu seinem Polabstand und dem Quadrat der Winkelgeschwindigkeit zu.
Die Beschleunigung eines Partikels 90° gegen den Uhrzeigersinn quer zur Richtung vom Beschleunigungspol zum Partikel nimmt proportional zu seinem Polabstand und zur Winkelbeschleunigung des Starrkörpers zu.

Die Lage des Beschleunigungspols interessiert in der Kinematik von Fahrzeugen, Getriebelehre und Robotik.

Beschleunigungspol in der komplexen Zahlenebene

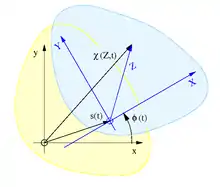
Rastebene (gelb) mit Rastkoordinaten (schwarz) und Gangebene (himmelblau) mit Gangkoordinaten (blau)

Der Beschleunigungspol wird nur bei ebenen Bewegungen betrachtet und daher kann die Starrkörperbewegung als Bewegung der komplexen Zahlenebene modelliert werden. Der feststehende Bildraum ist die Rastebene, die den Raum unserer Anschauung repräsentiert und die das Rastkoordinatensystem enthält. Der bewegte Urbildraum ist die Gangebene, die den in der Gangebene ruhenden Starrkörper und das Gangkoordinatensystem beinhaltet. Alle Partikel des Starrkörpers bewegen sich also mit der Gangebene mit. In Anlehnung an die eulersche- und die lagrangesche Betrachtungsweise werden die Koordinaten in der Rastebene mit Kleinbuchstaben und die Koordinaten in der Gangebene mit Großbuchstaben bezeichnet, siehe Bild.

Jeder Punkt in der komplexen Zahlenebene entspricht einer komplexen Zahl. Die Translation eines Punktes wird mit der Addition einer anderen Zahl und die Rotation um den Ursprung mit dem Produkt mit der komplexen Zahl $e^{\mathrm {i} \phi }$ modelliert, worin $\phi$ der Drehwinkel, e^x die e-Funktion und i die imaginäre Einheit ist.

Der aktuelle Ort z, die Geschwindigkeit ${\dot {z}}$ und Beschleunigung ${\ddot {z}}$ eines bestimmten Partikels Z des Starrkörpers in der Gangebene kann dann in der Rastebene zu

{\begin{aligned}\chi (Z,t)=&s+e^{\mathrm {i} \phi }Z=z\quad \rightarrow \quad {\dot {z}}={\dot {s}}+\mathrm {i} \omega e^{\mathrm {i} \phi }Z\\\rightarrow \quad {\ddot {z}}=&{\ddot {s}}+\mathrm {i} {\dot {\omega }}e^{\mathrm {i} \phi }Z-\omega ^{2}e^{\mathrm {i} \phi }Z={\ddot {s}}+(\mathrm {i} {\dot {\omega }}-\omega ^{2})(z-s)\end{aligned}}

berechnet werden, denn gemäß der ersten Beziehung ist $e^{\mathrm {i} \phi }Z=z-s$ . Der Punkt s bezeichnet den Bezugspunkt um den sich die Gangebene mit dem Starrkörper dreht und in dem der Ursprung des Gangkoordinatensystems liegt. Die Drehgeschwindigkeit und -beschleunigung ergibt sich aus den Zeitableitungen des Drehwinkels: $\omega ={\dot {\phi }},\,{\dot {\omega }}={\ddot {\phi }}$ . Der Beschleunigungspol p ist nun der Ort an dem ${\ddot {p}}$ verschwindet:

{\ddot {p}}={\ddot {s}}+(\mathrm {i} {\dot {\omega }}-\omega ^{2})(p-s)=0\quad \rightarrow \quad p=s+{\frac {\omega ^{2}+\mathrm {i} {\dot {\omega }}}{\omega ^{4}+{\dot {\omega }}^{2}}}{\ddot {s}}

Der Real- und Imaginärteil des Beschleunigungspols p sind eingangs angegeben worden. Wenn der Bezugspunkt nicht angetrieben wird, dann liegt der Beschleunigungspol im Bezugspunkt. Die Beschleunigung an einem beliebigen Ort ist

{\begin{aligned}{\ddot {z}}=&{\ddot {s}}+(\mathrm {i} {\dot {\omega }}-\omega ^{2})(z\underbrace {-p+p} _{=0}-s)=\underbrace {{\ddot {s}}+(\mathrm {i} {\dot {\omega }}-\omega ^{2})(p-s)} _{={\ddot {p}}=0}+(\mathrm {i} {\dot {\omega }}-\omega ^{2})(z-p)\\=&{\sqrt {\omega ^{4}+{\dot {\omega }}^{2}}}e^{\mathrm {i} \beta }(z-p)\end{aligned}}

Die Beschleunigung nimmt für alle Partikel im Starrkörper linear mit dem ${\sqrt {\omega ^{4}+{\dot {\omega }}^{2}}}$ -fachen des Abstandes zum Beschleunigungspol zu und schließt mit der Verbindungsstrecke zum Beschleunigungspol den Winkel

\beta =\arg(\mathrm {i} {\dot {\omega }}-\omega ^{2})=\arctan \left(-{\frac {\dot {\omega }}{\omega ^{2}}}\right)

ein. Darin ist arg die Argument-Funktion und arctan der Arcustangens. Der Winkel β dreht immer entgegengesetzt zur Winkelbeschleunigung.

Beispiel

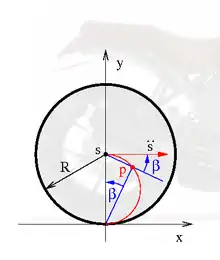
Nach rechts rollendes beschleunigtes Rad (schwarz) mit wanderndem Beschleunigungspol (rot)

Betrachtet wird das Hinterrad mit Radius R eines sich beschleunigenden Motorrades. Die Bewegung findet in der komplexen xy-Ebene parallel zur x-Achse in positiver x-Richtung statt. Der Aufstandspunkt des Rades ist zu Beginn der Ursprung, so dass die Hinterachse sich anfangs im Punkt s = s_x + is_y = i R befindet. Das Motorrad fahre mit konstanter positiver Beschleunigung a in Richtung der positiven x-Achse los. Dann ist die Beschleunigung des Motorrades gleich der Beschleunigung des Radmittelpunktes, der den Bezugspunkt abgibt:

a={\ddot {s}}={\ddot {s}}_{x}={\textsf {const.}}

Bei schlupflosem Abrollen des Hinterrades ist s_y=R=const. und

{\begin{array}{rcl}s_{x}&=&-R\phi \;\rightarrow {\dot {s}}_{x}=-R{\dot {\phi }}=-R\omega \;\rightarrow {\ddot {s}}_{x}=-R{\dot {\omega }}=a\\\rightarrow {\dot {\omega }}&=&-{\frac {a}{R}}\;\rightarrow \omega =-{\frac {at}{R}}\;\rightarrow \phi =-{\frac {at^{2}}{2R}}\end{array}}

denn das Hinterrad dreht im Uhrzeigersinn also mit negativer Drehgeschwindigkeit um die z-Achse. Damit berechnet sich der Beschleunigungspol zu

{\begin{aligned}p_{x}=&s_{x}+{\frac {\omega ^{2}{\ddot {s}}_{x}-{\dot {\omega }}{\ddot {s}}_{y}}{\omega ^{4}+{\dot {\omega }}^{2}}}=s_{x}+{\frac {R^{2}at^{2}}{R^{2}+a^{2}t^{4}}}\\p_{y}=&s_{y}+{\frac {\omega ^{2}{\ddot {s}}_{y}+{\dot {\omega }}{\ddot {s}}_{x}}{\omega ^{4}+{\dot {\omega }}^{2}}}=R-{\frac {R^{3}}{R^{2}+a^{2}t^{4}}}\end{aligned}}

\rightarrow \quad (p_{x}-s_{x})^{2}+\left(p_{y}-{\frac {R}{2}}\right)^{2}={\frac {R^{2}}{4}}

Der Beschleunigungspol liegt – so wie das Bild nahelegt – auf einem Kreis mit halbem Reifenradius zwischen dem Aufstandspunkt und dem Radmittelpunkt.

Das Verhältnis des horizontalen Abstandes des Beschleunigungspols zu seiner Höhe über der „Straße“ ist

{\frac {p_{x}-s_{x}}{p_{y}}}={\frac {R}{at^{2}}}=-{\frac {\dot {\omega }}{\omega ^{2}}}=\tan \;\beta

Der Winkel β misst gegen den Uhrzeigersinn und ist positiv. Anfangs, zur Zeit t=0, ist β=−90°, weil sich das Rad noch nicht dreht aber die Winkelbeschleunigung ungleich null ist. Der Aufstandspunkt des Rades ist dann der Beschleunigungspol und die Beschleunigung stellt sich wie das Geschwindigkeitsfeld eines gleichförmig rollenden Rades dar, siehe Momentanpol. Mit zunehmender Geschwindigkeit wandert der Beschleunigungspol auf dem Halbkreis in Richtung Radmittelpunkt. Der Winkel zwischen dem Beschleunigungspol, dem Aufstandspunkt und der y-Achse ist der Winkel β, der mit der Zeit gegen null geht, weil die Winkelbeschleunigung konstant ist, die Winkelgeschwindigkeit aber immer weiter zunimmt. Geometrische und kinematische Gründe bewirken, dass der Radmittelpunkt immer genau in x-Richtung angetrieben wird.

Wird nach dem Erreichen der Zielgeschwindigkeit nicht weiter beschleunigt, ist fortan ${\ddot {s}}=0$ und daher p=s: Der Beschleunigungspol springt in den Radmittelpunkt und alle Partikel des Rades werden mit der – von der gleichförmigen Rotation bekannten – Zentripetalbeschleunigung zum Radmittelpunkt und Beschleunigungspol hin gezogen.

Siehe auch

Bereissche Polkette

Einzelnachweise

Karl-Heinrich Grote, Beate Bender, Dietmar Göhlich (Hrsg.): Dubbel. Taschenbuch für den Maschinenbau. Springer-Verlag, Berlin, Heidelberg 2019, ISBN 978-3-662-54805-9, S. B22, doi:10.1007/978-3-662-54805-9 (eingeschränkte Vorschau in der Google-Buchsuche).

Literatur

H. Klepp: Technische Mechanik, Kinematik und Kinetik 1. Pro Business, 2013, ISBN 978-3-86386-476-7.
Roberto Marcolongo: Theoretische Mechanik. B. G. Teubner, Leipzig und Berlin 1911, S. 135 f. (archive.org [abgerufen am 28. Dezember 2020]).
Felix Klein und Conrad Müller: Encyklopädie der mathematischen Wissenschaften. Mechanik. 4. Band, 1. Teilband. B. G. Teubner, Leipzig 1908, S. 216 f. (archive.org [abgerufen am 27. Dezember 2020]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[dubbel-1] Karl-Heinrich Grote, Beate Bender, Dietmar Göhlich (Hrsg.): Dubbel. Taschenbuch für den Maschinenbau. Springer-Verlag, Berlin, Heidelberg 2019, ISBN 978-3-662-54805-9, S. B22, doi:10.1007/978-3-662-54805-9 (eingeschränkte Vorschau in der Google-Buchsuche).