Othello (Spiel)
Othello und Reversi sind zwei eng verwandte strategische Brettspiele für zwei Personen.
| Othello Reversi | |
|---|---|
 Othello Spielbrett | |
| Daten zum Spiel | |
| Autor | Lewis Waterman |
| Erscheinungsjahr | 1880er |
| Art | Brettspiel |
| Mitspieler | 2 |
| Dauer | 2–60 Minuten |
| Alter | Empfohlen ab 5 Jahren |
Geschichte
In den 1880er Jahren entwickelte der Engländer Lewis Waterman ein Brettspiel, das er Reversi (lat. „die Umgedrehten“) nannte. Es wurde auf einem Schachbrett mit 64 Feldern gespielt. Sein Spiel ähnelte dem Game of Annexation („Das Annexionsspiel“), das von dem Engländer John W. Mollett erfunden wurde. Mollets Spiel wurde jedoch auf einem kreuzförmigen Brett gespielt. Beide wohnten in London und beanspruchten, die wahren Erfinder zu sein. Es kam zu einem Rechtsstreit.[1][2]
Die älteste bekannte Quelle zu Watermans Reversi ist ein Zeitungsartikel vom 21. August 1886 in „The Saturday Review“. Nachdem 1888 Walter H. Peel unter dem Pseudonym „Berkeley“ einige Artikel über Reversi im Magazin „The Queen“ veröffentlichte, wurde das Spiel bekannter. Es folgten rasch weitere Veröffentlichungen, darunter ebenfalls von Peel das „Handbook of Reversi“, das 1888 von Watermans Firma Jacques and Sons herausgegeben wurde und das mehrere Neuauflagen in den folgenden Jahrzehnten erlebte.
Die Firma Ravensburger verkauft seit 1893 Reversi-Spielbretter und brachte mehrere familienfreundliche Ausgaben wie „Räuber und Gendarm“ oder „Dreh das Ding“ auf den Markt. Reversi, das ein eingetragenes Markenzeichen von Ravensburger ist, gehört somit zu den erfolgreichsten Spielen der Neuzeit. Auch im englischen Sprachraum ist Reversi stets bekannt geblieben. So beschäftigte sich z. B. der englische Spielehistoriker R. C. Bell mit Reversi, und der amerikanische Wissenschaftsjournalist Martin Gardner regte im April 1960 in der Zeitschrift "Scientific American" eine Diskussion über die kürzestmögliche Reversi-Partie an.
1971 meldete der Japaner Gorō Hasegawa (長谷川五郎) die Variante Othello in Japan als Warenzeichen an, ohne, wie er behauptete, Kenntnis von Reversi gehabt zu haben. Sein Vater war Englischlehrer und schlug, wegen der Analogie zu Shakespeares Othello, diesen Namen vor.
Die wichtigsten Unterschiede bestehen darin, dass bei Othello die ersten vier Steine als Eröffnung festgelegt sind, und bei Reversi jeder Spieler exakt nur 32 Steine hat. In Deutschland wird Reversi oft auch so gespielt, dass immer nur eine Reihe umgedreht wird. Ursprünglich wurde jedoch bei Reversi, ebenso wie in Othello, jede eingeschlossene Reihe erobert.
Heute ist Othello, neben Shōgi, Go und Renju, eines der beliebtesten Brettspiele in Japan, und es wird dort von etwa 25 Millionen Menschen gespielt. In Europa und Nordamerika blieb der große Erfolg aus. Stattdessen wird hier Reversi oft mit dem Hinweis verkauft, es mit modifizierten Regeln spielen zu können.
Othello ist das Spiel mit den meisten jährlichen Weltmeisterschaften (seit 1977) unter Lizenzregelungen. Bei Turnieren in Deutschland und in den Niederlanden werden meist Othello-Bretter verwendet, wie sie von der Firma Universal Trends in Deutschland vertrieben werden. Für Weltmeisterschaften werden die noch größeren Bretter des japanischen Verlegers Megahouse (früher Tsukuda) verwendet.
Mit der Entwicklung der Computer stieg auch die Spielqualität, und dank seiner einfachen Regeln findet Othello zunehmend Anklang als Computer- und Onlinespiel (meist aus Lizenzgründen unter dem Namen Reversi oder Neuschöpfungen wie „Drehum“ oder „Revello“ oder „Abtrünniger“; in der Nintendo Switch-Spielesammlung „51 Worldwide Games“). Seit der letzten Jahrhundertwende steigt mit Verbreitung des Internets auch deutlich die Anzahl der Freizeit- und der Turnierspieler.
Regeln
Auf einem 8×8-Brett legen die Spieler abwechselnd Spielsteine, deren Seiten unterschiedlich (schwarz und weiß) gefärbt sind. Ein Spieler („Weiß“) legt seinen Stein immer mit der weißen Seite nach oben, der andere („Schwarz“) entsprechend mit der schwarzen. Zu Spielbeginn befinden sich vier Steine in vorgegebener Anordnung auf dem Brett. Ein Spieler muss seinen Stein auf ein leeres Feld legen, das horizontal, vertikal oder diagonal an ein bereits belegtes Feld angrenzt. Wird ein Stein gelegt, werden alle gegnerischen Steine, die sich zwischen dem neuen Spielstein und einem bereits gelegten Stein der eigenen Farbe befinden, umgedreht. Spielzüge, die zu keinem Umdrehen von gegnerischen Steinen führen, sind nicht erlaubt. Das Ziel des Spiels ist es, am Ende eine möglichst große Anzahl von Steinen der eigenen Farbe auf dem Brett zu haben.
Die genauen Regeln:
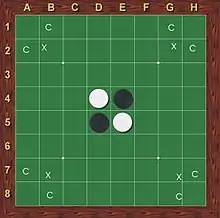
- Es wird auf einem Brett mit 8×8 Feldern gespielt.
- Bei der Variante Reversi hat am Anfang jeder Spieler einen Vorrat von 32 Steinen, bei Othello ist die Zahl der Steine unbegrenzt.
- Betrifft nur die Variante Othello: Als Startaufstellung werden vor dem Spielbeginn zwei weiße und zwei schwarze Steine auf die mittleren Felder des Bretts gelegt, je zwei diagonal gegenüberliegende mit der gleichen Farbe (Bild).
- Betrifft nur die Variante Reversi (Jacques and Sons): In den ersten zwei Zügen setzen beide Spieler jeweils einen ihrer Steine (Rot oder Schwarz) auf die vier Mittelfelder. Es können deshalb zwei verschiedene „Startaufstellungen“ entstehen.
- Betrifft nur die Variante Reversi (Ravensburger): Im ersten Zug setzen beide Spieler jeweils zwei ihrer Steine (Farben editionsabhängig, z. B. Rot und Grün, Weiß und Rot, Rot und Gelb) auf die vier Mittelfelder. Es können deshalb zwei verschiedene „Startaufstellungen“ entstehen, wobei der erste Spieler sich diese de facto aussuchen darf.
- Die Spieler ziehen abwechselnd, Schwarz beginnt (Jacques and Sons: Rot). Man setzt entweder einen Stein mit der eigenen Farbe nach oben auf ein leeres Feld, oder man passt. Passen ist aber nur erlaubt, wenn man keine regelkonforme Möglichkeit hat, einen Stein zu setzen.
- Man darf nur so setzen, dass ausgehend von dem gesetzten Stein in beliebiger Richtung (senkrecht, waagerecht oder diagonal) ein oder mehrere gegnerische Steine anschließen und danach wieder ein eigener Stein liegt. Es muss also mindestens ein gegnerischer Stein von dem gesetzten Stein und einem anderen eigenen Stein in gerader Linie eingeschlossen werden. Dabei müssen alle Felder zwischen den beiden eigenen Steinen von gegnerischen Steinen besetzt sein.
- Alle gegnerischen Steine, die so eingeschlossen werden, wechseln die Farbe, indem sie umgedreht werden. Dies geschieht als Teil desselben Zuges, bevor der Gegner zum Zug kommt. Ein Zug kann mehrere Reihen gegnerischer Steine gleichzeitig einschließen, die dann alle umgedreht werden. Wenn aber ein gerade umgedrehter Stein weitere gegnerische Steine einschließt, werden diese nicht umgedreht.
- Wenn die Spieler unmittelbar nacheinander passen, wenn also keiner mehr einen Stein setzen kann, ist das Spiel beendet. Beim Reversi ist dies der Fall, wenn beide Spieler entweder keine Steine mehr haben oder keine gegnerischen Steine mehr umdrehen können.
- Der Spieler, der am Ende die meisten Steine seiner Farbe auf dem Brett hat, gewinnt. Haben beide die gleiche Zahl, ist das Spiel unentschieden.
- Um die Höhe des Gewinns zu ermitteln, gibt es verschiedene Regelungen. Meist werden die Felder, die bei Spielende noch leer sind, dem Gewinner gutgeschrieben, also zu der Differenz der Steineanzahl addiert.
- Mit einer Zusatzregel, die oft in japanischen Turnieren angewandt wird, kann man ein Unentschieden vermeiden: Ein Spieler (der z. B. ausgelost wird) legt fest, ob eine gleiche Steineanzahl am Partieende als Sieg für Weiß oder für Schwarz gewertet wird. Der andere Spieler wählt dann eine Farbe.
Pragmatische Regeln für Partien ohne Computerunterstützung:
- Ein einmal gelegter Spielstein darf nicht mehr vom Brett genommen werden.
- Hat ein Spieler einen Stein zu Unrecht umgedreht oder vergessen, einen umzudrehen, kann dies von beiden Spielern korrigiert werden, bis der Gegenspieler seinen nächsten Zug gemacht hat. Danach bleiben falsch bzw. nicht umgedrehte Steine liegen.
Strategie
Stabilität

Einen Eckstein positioniert zu haben, bringt den Vorteil mit sich, dass dieser Stein nicht mehr vom Gegner erbeutet werden kann, da er nicht von gegnerischen Steinen umschlossen und somit umgedreht werden kann. Ein solcher Spielstein, der die Farbe nicht mehr wechseln kann, wird stabiler Stein ('stable disc') genannt, denn seine Farbe ist im weiteren Spielverlauf stabil. Ausgehend von einem stabilen Stein kann man häufig danebenliegende Steine annektieren, die ebenfalls zu stabilen Steinen werden können.
In Abb. stable discs sieht man die Ausgangsposition vor den letzten zwei Zügen. Weiß besitzt noch 20 Steine, von denen die Hälfte stabil ist und nicht mehr umgedreht werden kann. Die Steine der A- und der B-Spalte sowie die Achter-Reihe sind jedoch noch nicht stabil. Nun kann nur Schwarz ziehen und das auch nur auf A8. Sofort verliert Weiß die Steine B7, B8, C8 und D8. Diese Steine sind nun für Schwarz stabil. Mit dem letzten Zug nimmt Schwarz alle Steine der A-Spalte. Weiß verliert somit alle nicht-stabilen Steine.
X- und C-Felder
Einige Felder haben spezielle Bezeichnungen, da ihnen im Spiel besondere Bedeutung zukommt. Dies sind die Felder neben den Ecken: Das Feld auf der Diagonalen vor der Ecke wird X-Feld (B2, B7, G2, G7) genannt, die anderen beiden Felder, die an die Ecke grenzen, sind C-Felder (A2, B1, A7, B8, G1, H2, H7, G8).
Innerhalb des Spielfeldes werden verschiedene Regionen nach dem Prinzip der Himmelsrichtungen unterschieden. So wird die Region um die Ecke H1 als die Nord-Ost-Region bezeichnet.
Mobilität, Tempo, Mauern und leise Züge
Im letzten Abschnitt wurde der Wert des Besitzes von Ecken und allgemein stabilen Steinen sowie die Gefahr beim Setzen auf x- und c-Felder erklärt. Es gibt also bereits im Mittelspiel gute und schlechte Züge. Man kann damit das strategische Ziel formulieren, den Gegner zu schlechten Zügen zu zwingen und zu vermeiden, selbst zu schlechten Zügen gezwungen zu werden. Dies kann erreicht werden, indem man so zieht, dass einem selbst viele (gute) Züge bleiben oder eröffnet werden, dem Gegner jedoch nur wenige (schlechte) Züge zur Verfügung stehen; man sagt: die eigene Mobilität maximieren und die Mobilität des Gegners einschränken.
Diese Strategie ist extensiv in dem Sinn, dass, wenn zu einem Zeitpunkt die eigene Mobilität hoch und die des Gegners gering ist, man im Allgemeinen so flexibel ist, dass man einen Zug findet, der diesen Zustand erhält, wohingegen der Gegner schwer einen guten Zug finden wird, der seine Mobilität erhöht und die eigene herabsetzt. Sie ist deshalb von Beginn des Spiels an sinnvoll.
Gelingt es einem Spieler, ein sehr starkes Mobilitätsungleichgewicht zu seinen Gunsten herzustellen, so sagt man, er habe die Kontrolle gewonnen: Seinem Gegner bleiben immer nur sehr wenige Möglichkeiten, oder er muss gar aussetzen. Auf diese Weise verliert man als Anfänger gegen sehr überlegene Spieler oder gute Computerprogramme.
Othello ist also ein Spiel, in dem man oft gerne aussetzen würde: Jeder eigene Zug hat die Tendenz, dem Gegner neue Zugmöglichkeiten zu eröffnen und eigene Zugmöglichkeiten zu verbrauchen. Ziehe ich, so kann mein Gegner meist gut auf diesen Zug antworten, und ich habe erneut das Problem, mir einen Zug zu suchen. So sind Stellungen kaum zu bewerten, wenn nicht bekannt ist, wer am Zug ist: Im Allgemeinen ist eine gegebene Position schlechter für Weiß zu bewerten, wenn Weiß am Zug ist, als wenn Schwarz am Zug ist. Dieses Phänomen wird mit dem Begriff Tempo umschrieben: Man spricht von Tempogewinn, wenn man es schafft, die unangenehme Zugsuche auf den Gegner zu lenken. Ein Tempozug ist ein Zug, der schlecht zu beantworten ist und so den Gegner zur Zugsuche zwingt. Man hat einen Tempovorteil, wenn der Gegner am Zug ist und weniger oder genauso viele (!) Tempozüge wie man selbst zur Verfügung hat.
In Abb. Mobil1 ist eine Situation zu sehen, die die Konzepte Mobilität und Tempo illustriert: Schwarz kann sehr stark nach a7 ziehen: Dies schränkt die Mobilität von Weiß erheblich ein: Die Züge d8, g5 und d3 stehen nicht mehr zur Verfügung. Die Züge b7 und b8 sind sehr ungünstig, da sie sofort zum Verlust der Ecke a8 führen. Damit bleiben Weiß effektiv nur zwei Möglichkeiten: g6 und d2-e2-f2. Schwarz hat jedoch zwei Tempozüge a3 und a2 zur Verfügung, und Weiß ist am Zug! Deshalb werden Weiß als erstes die Züge ausgehen, und Weiß wird gezwungen sein, die Ecke a8 abzugeben.
Mauern und leise Züge sind Begriffe, die helfen, die Mobilitätsstrategie umzusetzen. Mauern in der eigenen Farbe sind ungünstig, da man dort selbst keine Zugmöglichkeiten hat, der Gegner aber schon. In Abb. Mobil2 wäre der Zug f8 für Schwarz desaströs, da Schwarz damit eine Mauer aufbauen und so die eigene Mobilität massiv reduzieren würde.
Ein leiser Zug (quiet move) ist ein Zug, der das Brett so wenig wie möglich verändert, typischerweise indem er nur einen Stein dreht, am besten einen inneren. Solche Züge sind günstig, da sie einem Aussetzen sehr nahe kommen und dem Gegner nur wenige neue Zugmöglichkeiten eröffnen. In Abb. Mobil3 kann Schwarz mit d3 einen leisen Zug spielen. Die Suche nach, die Vorbereitung von und das Vereiteln (Vergiften) von leisen Zügen ist vor allem charakteristisch für die Eröffnung.
 Mobil1: Mobilität und Tempo
Mobil1: Mobilität und Tempo Mobil2: Mauern
Mobil2: Mauern Mobil3: Leiser Zug
Mobil3: Leiser Zug
Kantenstrategie
Bei Steinen, die auf der Kante liegen, gibt es nur wenige angrenzende Felder und somit weniger Möglichkeiten, diese Steine umzudrehen. Außerdem bietet die Kante mit Hilfe der c-Felder, die auch auf ihr liegen, Zugang zur Ecke. Zusammen mit der Ecke kann man häufig auch einen Großteil der Kante übernehmen und dabei stabile Steine erhalten. Somit ist es wichtig, sich schon frühzeitig Gedanken zu machen, ob man seine Steine auf der Kante positionieren möchte, da eine eigene gute Kantenposition oder eine schwache Kantenposition des Gegners gegen Ende des Spiels einen großen Vorteil bedeuten kann.
Dabei ist es generell nicht unbedingt zu empfehlen, viele Steine auf der Kante zu haben – es ist sogar häufig ein Nachteil. Spielt z. B. Weiß zunächst zwei Steine so auf die Kante, dass nur ein Feld zwischen ihnen frei ist, kann Schwarz auf dieses freie Feld spielen und so einen Keil bekommen. Wie nützlich so ein Keil sein kann, erkennt man am Beispiel einer schwachen Kantenposition, den sogenannten unbalanced five, wie in Abb. Kante1 zu sehen. Nimmt Weiß in der gezeigten Stellung die Ecke, so kann sich Schwarz auf b8 einen Keil sichern und sich so die Möglichkeit schaffen, mit h8 die ganze Kante und die nächste Ecke zu übernehmen (siehe Abb. Kante2). Allerdings sind unbalanced five nicht immer von Nachteil. Hat nur Weiß Zugang zum freien c-Feld und Schwarz nicht, so kann Weiß einen Tempozug machen und damit gleichzeitig eine stabilere Kantenposition mit sechs Steinen erreichen. In diesem Fall ist diese Position also durchaus wünschenswert.
Auch ein Abstand von drei freien Feldern zwischen zwei eigenen Steinen kann sehr gefährlich sein. Betrachten wir eine Position mit weißen Steinen auf den Feldern c8 und g8. Schwarz kann nun mit einem Stein auf f8 drohen, die Ecke zu übernehmen, wie in Abb. Kante3 zu sehen. Verteidigt Weiß diesen Angriff über e8, bekommt Schwarz auf d8 einen Keil, mit dem er die Möglichkeit hat, die Ecke h8 zu erhalten (Abb. Kante4).
Grundsätzlich kann man also sagen, dass eine Kantenposition mit zwei eigenen Steinen mit ungeradem Abstand sehr viel leichter angreifbar ist als eine Position mit geradem Abstand. Allerdings muss man auch berücksichtigen, dass häufig das in der Theorie richtige Feld nicht spielbar ist, weil kein Zugang besteht. Dann muss man entweder versuchen, sich diesen Zugang zu verschaffen, oder einen alternativen Stein spielen.
 Kante 1: Weiß am Zug hat unbalanced five
Kante 1: Weiß am Zug hat unbalanced five Kante 2: Schwarz hat einen Keil auf b8 und kann die Ecke h8 und die Kante übernehmen
Kante 2: Schwarz hat einen Keil auf b8 und kann die Ecke h8 und die Kante übernehmen Kante 3: Schwarz hat f8 gespielt und droht, sich die Ecke h8 zu sichern
Kante 3: Schwarz hat f8 gespielt und droht, sich die Ecke h8 zu sichern Kante 4: Weiß hatte keine Chance, den Keil und damit den Eckenverlust abzuwenden
Kante 4: Weiß hatte keine Chance, den Keil und damit den Eckenverlust abzuwenden
Parität
Zu Ende des Spiels entstehen meist kleinere Regionen. Diese Regionen sind Gruppen freier Felder, meistens zwischen zwei und sechs Steinen, die sich gewöhnlich um das Eckfeld herum befinden. Der Spieler, der in einer solchen Region den letzten Zug macht, hat einen Vorteil, da er als Letzter Steine umdrehen darf und diese eher stabil sind.
In Abb. Parität1 sind nur noch zwei Steine zu spielen und Schwarz ist am Zug. Egal wohin Schwarz setzt, er verliert 28 zu 36. Sollte Weiß am Zug sein, so gewinnt Schwarz mit 36 zu 28. Hieraus ergibt sich, dass Weiß im Endspiel einen kleinen Vorteil besitzt, da es normalerweise den letzten Stein setzt. Schwarz kann diesen Vorteil umgehen, indem innerhalb des Spiels einmal ausgesetzt wird. Bei einer geraden Anzahl von ausgesetzten Zügen hebt sich der Vorteil logischerweise wieder auf. Da es in der Regel sehr schwer ist, einen Spieler zum Aussetzen zu zwingen, gibt es noch eine weitere Möglichkeit, Parität zu seinen Gunsten zu beeinflussen. Hierfür muss ein Spieler es schaffen, dass sein Gegner in einer Region nicht spielen kann. Der Spieler bekommt also mehrere Züge in Folge in einer Region. In Bezug auf Parität bedeutet dies, dass der Spieler versuchen sollte zu erzwingen, dass er den letzten Stein in einer Region setzen kann. Wenn mehrere Regionen frei sind, so kann er auch die Parität in anderen Regionen zu seinen Gunsten beeinflussen.
Wie man in Abb. Parität2 sieht, hat der weiße Spieler keine Möglichkeit, in die untere rechte Region zu spielen. Wenn Schwarz nun in diese Region setzt, kann Weiß Parität für die anderen beiden Regionen erzwingen, indem es anschließend einen Stein in die obere rechte Ecke setzt. Egal in welche Region Schwarz spielt, Weiß hat den letzten Zug und gewinnt mit 38 zu 26. Wenn Schwarz stattdessen g2 spielt und die Ecke h1 freiwillig abgibt, so erzwingt er Parität in allen drei Regionen. Wenn also g2-h1-g1-a1-a2 gespielt werden, so endet Schwarz nun mit g8 und gewinnt 37 zu 27.
Oftmals ist auch der beste Zug nicht direkt ersichtlich. In Abb. Parität3 führt der Zug b7 dazu, dass Weiß b8 setzt, ohne Schwarz Zugang zu a8 zu ermöglichen. Schwarz müsste in eine andere Region spielen und dementsprechend die Parität in allen vier Regionen aufgeben. Schwarz würde 22 zu 42 verlieren. Spielt Schwarz hingegen den wenig intuitiven Zug b2, so verliert es zwar eine Ecke, kann aber nach dem Zug des weißen Spielers, der vermutlich nach a1 gehen wird, nach b7 spielen. Weiß kann in der linken unteren Region nun Schwarz nicht mehr blocken. Schwarz erhält den letzten Zug und damit Parität. Da Schwarz den letzten Zug in der Region hat, muss Weiß nun zuerst in die anderen Regionen spielen. Schwarz hat sich also die Parität in drei von vier Regionen erspielt und gewinnt 40 zu 24.
 Parität1: Nur noch zwei Steine zu spielen
Parität1: Nur noch zwei Steine zu spielen Parität2: Schwarz ist am Zug
Parität2: Schwarz ist am Zug Parität3: Schwarz ist am Zug
Parität3: Schwarz ist am Zug
Endspiel

Als Endspiel bezeichnet man den letzten Spielabschnitt, in dem der größte Teil des Bretts bereits mit Steinen besetzt ist. Frei geblieben sind meist u. a. die bislang unerreichbaren Ecken sowie ein Teil der x- und c-Felder, die von den Spielern gemieden worden sind, um dem Gegner keinen Zugang zur Ecke zu gewähren.
Im Mittelspiel ist die abschließende Bewertung einer Stellung meist nicht möglich, weil dazu eine mit der noch auszuführenden Anzahl von Zügen exponentiell wachsende Zahl möglicher Spielverläufe untersucht werden müsste. Da dies selbst Rechner und geübte Spieler überfordern würde, kann nur eine Abschätzung der Gewinnchancen anhand von Kriterien wie Stabilität, Mobilität oder Parität erfolgen. Im Endspiel dagegen ist die Zahl der Zugmöglichkeiten sowie der insgesamt noch auszuführenden Züge so weit gesunken, dass der weitere Spielverlauf überschaubar wird. Wegen fehlender anderer Zugmöglichkeiten wird irgendwann im Spiel einer der Spieler gezwungen sein, seinem Gegner zum Beispiel durch Besetzung eines x-Feldes Zugang zu einer Ecke zu verschaffen. Um die negativen Folgen eines solchen Eckverlusts in Grenzen zu halten, sind Kombinationen beliebt, die zu einem Eckentausch führen. Ein Spieler opfert dabei dem Gegner eine Ecke, um anschließend selbst eine andere Ecke einzunehmen. Dadurch lässt sich oftmals gleichziehen oder im Hinblick auf die Besetzung der Ränder sogar ein Vorteil erzielen.
Ein beliebtes Angriffsziel bei einem Angebot zum Eckentausch ist die schon im Abschnitt zur Kantenstrategie erwähnte Anordnung der unbalanced five. Der Gegner opfert durch Besetzung des x-Feldes neben dem noch freien c-Feld eine Ecke, um danach einen eigenen Stein als Keil auf das c-Feld zu setzen und später auch noch die andere Ecke sowie die gesamte Kante als stabile Steine zu übernehmen. Allerdings gelingt dieser Schlag nur, wenn der Gegner das Opfer auch annimmt und die ihm angebotene Ecke besetzt. Solange er bessere Züge zur Auswahl hat, sollte er es ablehnen. Für den anbietenden Spieler ist die Besetzung des x-Feldes aber trotzdem noch ein evtl. entscheidender Tempozug.
Ein Spielmanöver, das den Eckentausch um eine schwache Randaufstellung des Gegners erzwingt, ist die Stoner-Trap (siehe Abb. Stoner Trap). Das Eckenopfer wird vorbereitet, indem Weiß mit dem Zug b7 die Hauptdiagonale unter Kontrolle bringt. Dies ist wichtig, weil die Stoner-Trap noch einen zweiten Vorbereitungszug erfordert und der Gegner nicht sofort die Ecke besetzen darf. Dreht Schwarz im nächsten Zug (z. B. nach b3) einen Stein in der Hauptdiagonale um und droht mit der Besetzung der Ecke a8, so antwortet Weiß mit dem Angriffszug c8 und droht nun seinerseits mit der Besetzung der Ecke h8. Nimmt Schwarz die Ecke a8, so antwortet Weiß mit b8 und lässt später h8 folgen, wodurch es sieben stabile Steine erhält. Will Schwarz mit b8 den Zug von Weiß nach h8 verhindern, kommt es noch schlimmer und Weiß erhält mit a8 und anschließend h8 beide Ecken und die gesamte Kante. Ein anderer Zug als a8 oder b8 hilft wegen der Drohung von Weiß, die Ecke h8 zu besetzen, auch nicht weiter. Beim Stellen der Stoner-Trap ist jedoch äußerste Aufmerksamkeit geboten. Können die Züge nicht wie im Geiste vorausberechnet ausgeführt werden, kann die geopferte Ecke ohne Ausgleich verloren gehen.
Othello-Weltmeisterschaft
| Jahr | Ort | Weltmeister | Land | Team | 2. Platz | Land | Weltmeisterin | Land |
|---|---|---|---|---|---|---|---|---|
| 1977 | Tokio | Hiroshi Inoue | Japan | N/A | Thomas Heiberg | Norwegen | ||
| 1977* | Monte Carlo | Sylvain Perez | Frankreich | N/A | Michel Rengot (Blanchard) | Frankreich | ||
| 1978 | New York City | Hidenori Maruoka | Japan | N/A | Carol Jacobs | USA | ||
| 1979 | Rom | Hiroshi Inoue | Japan | N/A | Jonathan Cerf | USA | ||
| 1980 | London | Jonathan Cerf | USA | N/A | Takuya Mimura | Japan | ||
| 1981 | Brüssel | Hidenori Maruoka | Japan | N/A | Brian Rose | USA | ||
| 1982 | Stockholm | Kunihiko Tanida | Japan | N/A | David Shaman | USA | ||
| 1983 | Paris | Ken’ichi Ishii | Japan | N/A | Imre Leader | Großbritannien | ||
| 1984 | Melbourne | Paul Ralle | Frankreich | N/A | Ryoichi Taniguchi | Japan | ||
| 1985 | Athen | Masaki Takizawa | Japan | N/A | Paolo Ghirardato | Italien | ||
| 1986 | Tokio | Hideshi Tamenori | Japan | N/A | Paul Ralle | Frankreich | ||
| 1987 | Mailand | Ken’ichi Ishii | Japan | USA | Paul Ralle | Frankreich | ||
| 1988 | Paris | Hideshi Tamenori | Japan | Großbritannien | Graham Brightwell | Großbritannien | ||
| 1989 | Warschau | Hideshi Tamenori | Japan | Großbritannien | Graham Brightwell | Großbritannien | ||
| 1990 | Stockholm | Hideshi Tamenori | Japan | Frankreich | Didier Piau | Frankreich | ||
| 1991 | New York City | Shigeru Kaneda | Japan | USA | Paul Ralle | Frankreich | ||
| 1992 | Barcelona | Marc Tastet | Frankreich | Großbritannien | David Shaman | Großbritannien | ||
| 1993 | London | David Shaman | USA | USA | Emmanuel Caspard | Frankreich | ||
| 1994 | Paris | Masaki Takizawa | Japan | Frankreich | Karsten Feldborg | Dänemark | ||
| 1995 | Melbourne | Hideshi Tamenori | Japan | USA | David Shaman | USA | ||
| 1996 | Tokio | Takeshi Murakami | Japan | Großbritannien | Stéphane Nicolet | Frankreich | ||
| 1997 | Athen | Makoto Suekuni | Japan | Großbritannien | Graham Brightwell | Großbritannien | ||
| 1998 | Barcelona | Takeshi Murakami | Japan | Frankreich | Emmanuel Caspard | Frankreich | ||
| 1999 | Mailand | David Shaman | Niederlande | Japan | Tetsuya Nakajima | Japan | ||
| 2000 | Kopenhagen | Takeshi Murakami | Japan | USA | Brian Rose | USA | ||
| 2001 | New York City | Brian Rose | USA | USA | Raphael Schreiber | USA | ||
| 2002 | Amsterdam | David Shaman | Niederlande | USA | Ben Seeley | USA | ||
| 2003 | Stockholm | Ben Seeley | USA | Japan | Makoto Suekuni | Japan | ||
| 2004 | London | Ben Seeley | USA | USA | Makoto Suekuni | Japan | ||
| 2005 | Reykjavík | Hideshi Tamenori | Japan | Japan | Kwangwook Lee | Südkorea | Hisako Hoshi | Japan |
| 2006 | Mito | Hideshi Tamenori | Japan | Japan | Makoto Suekuni | Singapur | Toshimi Tsuji | Japan |
| 2007 | Athen | Kenta Tominaga | Japan | Japan | Stéphane Nicolet | Frankreich | Yukiko Tatsumi | Japan |
| 2008 | Oslo | Michele Borassi | Italien | Japan | Tamaki Miyaoka | Japan | Liya Ye | Deutschland |
| 2009 | Gent | Yusuke Takanashi | Japan | Japan | Matthias Berg | Deutschland | Mei Urashima | Japan |
| 2010 | Rom | Yusuke Takanashi | Japan | Japan | Michele Borassi | Italien | Jiska Helmes | Niederlande |
| 2011 | Newark, NJ | Hiroki Nobukawa | Japan | Japan | Piyanat Aunchulee | Thailand | Jian Cai | USA |
| 2012 | Leeuwarden | Yusuke Takanashi | Japan | Japan | Kazuki Okamoto | Japan | Veronica Stenberg | Schweden |
| 2013 | Stockholm | Kazuki Okamoto | Japan | Japan | Piyanat Aunchulee | Thailand | Katie Wu | Finnland |
| 2014[3] | Bangkok | Makoto Suekuni | Japan | Japan | Ben Seeley | USA | Joanna William | Australien |
| 2015 | Cambridge | Yusuke Takanashi | Japan | Japan | Makoto Suekuni | Japan | Yoko Sano | USA |
| 2016 | Mito | Piyanat Aunchulee | Thailand | Japan | Yan Song | China | Zhen Dong | China |
| 2017 | Gent | Yusuke Takanashi | Japan | Japan | Akihiro Takahashi | Japan | Misa Sugawara | Japan |
| 2018 | Prag | Keisuke Fukuchi | Japan | Japan | Piyanat Aunchulee | Thailand | Misa Sugawara | Japan |
| 2019 | Tokio | Akihiro Takahashi | Japan | Japan | Yusuke Takanashi | Japan | Joanna William | Australien |
*Die rivalisierende WM in Monte Carlo gilt meist nicht als offiziell und wird oft auf offiziellen Seiten als erste Europa-Meisterschaft bezeichnet.
Computer-Othello
Siehe auch
- Ataxx, ganz andere Regeln und Strategie, aber fast gleiches Spielbrett, gleiche Spielsteine und gleiches Ziel.
Literatur
- Erwin Glonnegger: Das Spiele-Buch: Brett- und Legespiele aus aller Welt; Herkunft, Regeln und Geschichte. Drei-Magier-Verlag, Uehlfeld 1999. ISBN 3-9806792-0-9.
- Michael Buro: Techniken für die Bewertung von Spielsituationen anhand von Beispielen. Dissertation, Universität Paderborn, 1994.
- Paul S. Rosenbloom: A world-championship-level Othello program. In: Artificial Intelligence. Bd. 19, Nr. 3, 1982, ISSN 0004-3702, S. 279–320.
- Kai-Fu Lee and Sanjoy Mahajan: The development of a world class Othello program. In: Artificial Intelligence. Bd. 43, Nr. 1, 1990, ISSN 0004-3702, S. 21–36.
Weblinks
- Othello-Club Deutschland
- World Othello Federation (englisch)
- Reversi / Othello bei der Europäischen Spielesammler Gilde
- Othello in der Spieledatenbank BoardGameGeek (englisch)
Einzelnachweise
- Martin Gardener: Mathematische Knobeleien. Springer Verlag, 2013, Seite 56. Abgerufen am 27. Mai 2020
- Vintage Othello and Reversi. retrowow.uk, abgerufen am 27. Mai 2020
- Trees van Seggelen: WOC 2014 Results. 29. November 2014, abgerufen am 5. Mai 2015 (englisch).