Maximum Power Point Tracking

Unter dem Begriff Maximum Power Point Tracking, MPP-Tracking oder MPPT (auf deutsch etwa „Maximal-Leistungspunkt-Suche“) bezeichnet man in der Elektrotechnik, speziell in der Photovoltaik, ein Verfahren, bei dem die elektrische Belastung einer Solarzelle, eines Solarmoduls oder von mehreren in Reihe geschalteten Solarmodulen („string“, deutsch auch „Strang“) so angepasst wird, dass den Zellen die größte mögliche Leistung entnommen werden kann. Bei Solarzellen ist dieser optimale Betriebspunkt nicht konstant, sondern hängt unter anderem von der Bestrahlungsstärke, der Temperatur am Solarmodul und dem Typ der Solarzellen ab.

Motivation

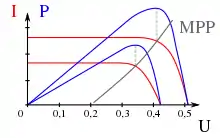
Verschiebung des MPP mit sich ändernder Bestrahlungsstärke sowie Strom und Leistung im Bezug zur Spannung

Allgemein kann die größte mögliche Leistung dann aus einer elektrischen Quelle entnommen werden, wenn das Produkt von elektrischem Strom I und elektrischer Spannung U sein Maximum hat, dies entspricht dem Fall, dass der Innenwiderstand der Quelle gleich dem externen Lastwiderstand ist. Dieser Betriebspunkt wird allgemein als Leistungsanpassung (englisch Maximum Power Point, MPP) bezeichnet und ist in nebenstehendem Diagramm für eine Solarzelle in der schwarzen Kurve MPP abgebildet. In Blau sind zwei beispielhafte Betriebszustände mit der jeweiligen maximalen Leistung P im Schnittpunkt eingezeichnet.

Bei Solarzellen ist der Innenwiderstand oder der optimale Betriebspunkt mit maximaler Leistungsabgabe nicht konstant, sondern hängt von externen Faktoren wie der momentanen Bestrahlungsstärke und der Temperatur des Moduls ab. Daher wird der Lastwiderstand des Solarmoduls durch eine elektronisch gesteuerte Schaltung so beeinflusst, dass der Lastwiderstand laufend so eingestellt und nachgeführt wird, dass er fast exakt gleich dem momentanen Innenwiderstand der Solarzelle ist und damit die Leistungsabgabe des Solarmoduls unter verschiedenen Betriebsbedingungen immer maximal ist.

In der Praxis erfolgen die Einstellung des optimalen Betriebspunktes und dessen laufende Nachführung durch eine elektronische Schaltung, das MPP-Tracking – im Prinzip ein speziell auf diese Aufgabe optimierter Gleichspannungswandler. Dieser wird auf seiner Eingangsseite mit der Solarzelle verbunden, die bei veränderlichem Innenwiderstand durch den MPP-Trackingalgorithmus stets mit Leistungsanpassung betrieben wird. Auf der Ausgangsseite muss diese maximal gewonnene Leistung abgenommen werden; meist wird ein Akku geladen, dessen Spannung sich nur langsam ändert, dessen Ladestrom aber entsprechend der gelieferten Leistung schwankt. Eine direkte Versorgung eines Verbrauchers ist nur möglich, wenn dieser die gesamte momentan erzeugte Leistung abnehmen kann. Am Wechselrichter muss stets die gesamte Leistung in ein Netz abgegeben werden können. Der Anschluss nur eines Verbrauchers (Inselnetz) ist ohne Akkupuffer nicht möglich. Bei Solarwechselrichtern sind die Funktionen MPP-Tracking und Wechselrichter in einem Gerät vereint.

Definitionen

Betrachtung eines gleichmäßig beleuchteten Solarmoduls

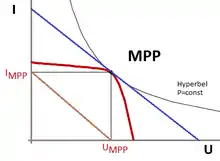
Erkennungsmerkmale in der Strom-Spannungs-Kennlinie

Strom-Spannungsdiagramm und Darstellung des Solarmoduls als Diodenkennlinie

Das Strom-Spannungsdiagramm, wie nebenstehend dargestellt, wird typischerweise so aufgetragen, dass die technische Stromrichtung des gemessenen Stroms in Sperrrichtung der Solarzelle zeigt. Der Strom wird damit bei Beleuchtung, im Gegensatz zur klassischen Diodenkennlinie, positiv aufgetragen.

Das Verhältnis zwischen der maximalen Leistung P_MPP der Solarzelle am Maximum Power Point und dem Produkt aus Leerlaufspannung U_L und Kurzschlussstrom I_K wird Füllfaktor FF genannt:

FF={\frac {P_{\rm {MPP}}}{U_{\rm {L}}\cdot I_{\rm {K}}}}

mit der Funktion der Leerlaufspannung des Solarmoduls:

U_{\rm {L}}=m\cdot U_{\rm {T}}\cdot \ln \left({\frac {I_{\rm {Ph}}}{I_{\rm {S}}}}+1\right)

m

= Diodenfaktor

U_{\rm {L}}

= Leerlaufspannung

I_{\rm {S}}

= Sättigungsstrom

U_{\rm {T}}

= Temperaturspannung

I_{\rm {Ph}}

= Photostrom

Der Photostrom steigt mit steigender Temperatur leicht an und wird in der Praxis meist vernachlässigt. Bei steigender Bestrahlung des Solarmoduls steigt der Strom annähernd proportional, die Leistung nimmt zu. Die Spannung ändert sich dabei kaum. Bei steigender Temperatur fällt die Spannung leicht ab, weil der Sättigungsstrom, auch Dunkelstrom genannt, ansteigt.

Die Leistung, die sich aus dem Produkt der Spannung und dem Strom ergibt, sinkt demnach bei konstanter Einstrahlung und steigender Modultemperatur. Typisch Werte sind −0,45 % pro Kelvin für kristalline Siliziumsolarzellen.

Als Erkennungsmerkmale für die erfolgreiche Leistungsanpassung werden in der Strom-Spannungs-Kennlinie folgende Eigenschaften ermittelt:

Es gilt bei Leistungsanpassung im MPP: ${\frac {\mathrm {d} I}{\mathrm {d} U}}=-{\frac {I}{U}}$
Im MPP berührt die I-U-Kennlinie die Hyperbel mit P = P_mpp = const.
Der MPP teilt seine Tangente in zwei gleich lange Abschnitte.
Die Diagonale im Rechteck der Punktkoordinaten ist parallel zur Tangente.

Die Erkennungsmerkmale sind auf die Eigenschaft der lokal maximalen Leistung zurückzuführen (Anstieg dp/dU=0). Sie sind gut geeignet, um in den Kennlinien auch ohne Leistungsachse die Position der MPPs zu bestimmen oder zu überprüfen. Sie sind auch anwendbar, wenn die Achsenskalierung fehlt.

Betrachtung mehrerer in Reihe geschalteter Solarmodule mit teilweiser Verschattung

UP-Kennlinie eines teilverschatteten Solargenerators. Lokaler und globaler MPP sind rot bzw. grün markiert.

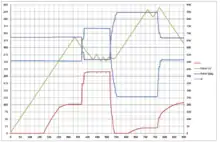
In den nebenstehenden Abbildungen ist ein String aus zehn in Reihe geschalteten Solarmodulen dargestellt: Die blau gestrichelte Kurve steht für den Fall, dass alle Module gleichmäßig bestrahlt sind. Die schwarze Kurve steht für den Fall, dass zwei der zehn Module im Schatten liegen, und nur noch 20 % der Einstrahlung im Vergleich zu den übrigen Modulen (durch diffuse Strahlung) erhalten.

Es ist ersichtlich, dass es im verschatteten Fall nicht mehr nur ein Leistungs-Maximum gibt, sondern mehrere. Grün markiert ist der „globale MPP“, also der tatsächliche Punkt maximaler Leistung. Rot markiert ist der „lokale MPP“, also ein lokaler Hochpunkt auf der Leistungs-Kennlinie.

Die Ursache dieses Verlaufs liegt in den Bypassdioden, die in die Solarmodule zum Schutz der einzelnen Zellen integriert sind: Am lokalen MPP werden alle Module mit demselben niedrigen Strom betrieben, den auch die verschatteten Module (durch diffuse Bestrahlung) noch liefern können. Erst wenn die Spannung gesenkt bzw. der Strom erhöht wird, sprechen die Bypassdioden der verschatteten Module an und schließen diese Modulteile kurz, überbrücken sie also. Dadurch ist die Stringspannung niedriger (die verschatteten Module „fehlen“ faktisch im String), aber der Strom deutlich höher, was die höhere Leistung am globalen Maximum erklärt.

UI-Kennlinie eines teilverschatteten Solargenerators.

Technische Verfahren

Schattenmanagement

Sämtliche unten beschriebene Methoden suchen den MPP in relativ kleinen Schritten rund um das aktuelle Leistungsmaximum. Dies hat den Vorteil, dass der Solargenerator die meiste Zeit sehr nahe am MPP betrieben wird (hoher MPP-Anpassungswirkungsgrad). Der Nachteil ist, dass der Tracker bei einem teilverschatteten Solargenerator oftmals am lokalen MPP verharrt (s. o.), ohne den Weg zum globalen MPP zu finden.

Deshalb haben die meisten Wechselrichter-Hersteller[1] inzwischen eine zusätzliche Funktion integriert, die in regelmäßigen Abständen (meist alle 5–10 Minuten) sehr schnell die gesamte Kennlinie des Solargenerators durchfährt, um nach dem globalen MPP zu suchen. Diese Funktion wird als Schattenmanagement oder Verschattungsmanagement bezeichnet, teilweise auch als Sweeping-Funktion, und ersetzt nicht das fortlaufende MPP-Tracking.

Bei der Mehrzahl der Hersteller ist die Funktion ab Werk aktiviert, bei anderen kann sie im Menü aktiviert werden[1]. Der Ertragsverlust durch das regelmäßige Durchfahren der Kennlinie (währenddessen der Generator naturgemäß nicht im MPP betrieben wird) ist beispielsweise mit kleiner 0,2 % angegeben[2], als Dauer für das Durchfahren der Kennlinie werden beispielsweise 2 Sekunden genannt[3].

Zu beachten ist, dass der Eingangsspannungsbereich des Wechselrichters ein limitierender Faktor sein kann: Nur wenn die Anzahl der unverschatteten Module genügt, um allein mit diesen Modulen die Mindest-Eingangsspannung des Wechselrichters zu erreichen, kann dieser den globalen MPP ansteuern. Daher ist es bei Verschattungsrisiko wichtig, ausreichend lange Strings zu installieren. Das frühere Vorgehen, bei Verschattungsgefahr viele kurze Strings zu installieren, ist seit Einführung des Schattenmanagements überholt.

Methode der Spannungserhöhung

Regelverhalten eines selbst gebauten MPP-Regler an einer simulierten Solarzelle. Zu sehen ist, wie der Regler die Belastung (grüne Kurve, Pulsweitenmodulation) nach Änderung der (simulierten) Solarspannung nachführt und bei Erreichen der optimalen Belastung (errechnete violette Kurve) diese zu oszillieren beginnt.

Bei der einfachsten Art der Suche nach dem Leistungsmaximum erhöht der MPP-Tracker kontinuierlich die Spannung der Solarzelle von null weg, wodurch die abgegebene Leistung steigt. Wird nun das Leistungsmaximum erreicht, so beginnt die Leistung wieder zu sinken, was als Abbruchkriterium für die Suche dient. Dieses iterative Verfahren führt ein Mikroprozessor im MPP-Tracker periodisch aus, sodass auch bei wechselnden Bestrahlungsverhältnissen immer ein Betrieb im maximalen Leistungspunkt vorliegt.

Methode der Lastsprünge

Bei der Methode der Lastsprünge (englisch Perturb and observe) ändert der Regler periodisch die Belastung der Solarzelle in kleinen Schritten (Lastsprung) in eine bestimmte Richtung und misst anschließend die von der Solarzelle abgegebene Leistung. Ist die nun gemessene Leistung höher als die gemessene Leistung der vorangegangenen Periode, so behält der Regler diese Suchrichtung bei und übt den nächsten Leistungssprung aus. Ist die gemessene Leistung kleiner als die der letzten Messperiode, so ändert der Regler die Suchrichtung und führt nun Lastsprünge in entgegengesetzter Richtung aus. Auf diese Weise wird das Leistungsmaximum permanent gesucht, was zur Folge hat, dass der exakte Punkt der maximalen Leistung nie gefunden wird, man sich ihm aber bis auf 1 Lastsprung annähert, was unproblematisch ist, wenn er klein genug ist. Es entsteht eine Art Oszillation um das Leistungsmaximum.[4] Bei einem teilverschatteten Solargenerator verharrt der Regler beim lokalen Maximum, falls er sich (zufällig) bei diesem befindet.

Steigende Konduktanz

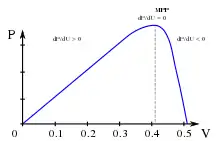
Darstellung der Leistungskurve mit Veranschaulichung der Bedingungen

Die Idee der Methode der steigenden Konduktanz (englisch Incremental conductance) beruht darauf, anhand des differenziellen sowie des konkreten Leitwertes der Solarzelle das Leistungsmaximum zu finden. Der maximale Leistungspunkt charakterisiert sich dadurch, dass die Änderung der abgegebenen Leistung in Relation zur Änderung der Spannung null wird. Je nachdem auf welcher Seite der Leistungskurve sich der aktuelle Belastungspunkt befindet, steigt oder sinkt das Leistungs-Spannungsverhältnis bei Änderung der Belastung, wodurch sich folgende Gleichungen ergeben:[5]

Links neben dem Maximum:

{\frac {dP}{dU}}>0

Rechts neben dem Maximum:

{\frac {dP}{dU}}<0

Im Leistungsmaximum:

{\frac {dP}{dU}}=0

Durch Umformen der Gleichungen erhält man folgende Bedingungen für den Regler, wobei I und U die aktuellen Messwerte der Regelperiode sind und dI, dU die Änderungen zur vorangegangenen Regelperiode.

Links neben dem Maximum:

{\frac {dI}{dU}}>-{\frac {I}{U}}

Rechts neben dem Maximum:

{\frac {dI}{dU}}<-{\frac {I}{U}}

Im Leistungsmaximum:

{\frac {dI}{dU}}=-{\frac {I}{U}}

Der Regler ändert nun anhand dieser Bedingung die Belastung pro Regelzyklus schrittweise in jene Richtung, in der er sich der Bedingung vom angestrebten Leistungsmaximum nähert. Erfüllt das System nun diese Bedingung, wurde das Leistungsmaximum gefunden, und die Suche kann beendet werden. Ändert sich aufgrund der Beleuchtungsintensität der Solarzelle die abgegebene Leistung, nimmt der Regler die Suche wieder auf.

Bei einem teilverschatteten Solargenerator verharrt der Regler beim lokalen Maximum, falls er sich (zufällig) bei diesem befindet.

Methode der konstanten Spannung

Die Methode der konstanten Spannung (englisch constant voltage) beruht darauf, dass zwischen der Leerlaufspannung der Solarzelle und jener Spannung, bei der die Solarzelle die maximale Leistung abgibt, ein Zusammenhang besteht. Somit kann anhand der Kenntnis über die Leerlaufspannung auf die für die Entnahme der maximal möglichen Leistung nötige Belastungsspannung und somit auf die Belastung geschlossen werden. Da sich die Leerlaufspannung anhand unterschiedlicher Parameter ändert, muss der Regler diese während des Betriebs periodisch messen. Hierzu wird für die Dauer der Spannungsmessung die Last von der Solarzelle getrennt. Anhand der nun gemessenen Leerlaufspannung kann der Regler die optimale Belastung berechnen und diese bei Wiederverbinden von Last und Solarzelle einstellen. Da der Zusammenhang zwischen Leerlaufspannung und optimaler Belastungsspannung empirisch vorab ermittelt wird und von vielen Parametern abhängt, wird das exakte Leistungsmaximum nicht erreicht. Der Algorithmus ist im engeren Sinne also keiner, der das eigentliche Leistungsmaximum sucht, und funktioniert nicht bei teilverschattetem Solargenerator.

Methode der Temperatur

Bei der Methode der Temperatur wird die Leerlaufspannung durch das Messen von der Temperatur am Solarmodul geschätzt.[6]

Der Algorithmus berechnet die folgende Gleichung:

U_{\mathrm {mpp} }(T)=U_{\mathrm {mpp} }(T_{\mathrm {ref} })+u_{V_{\mathrm {mpp} }}(T-T_{\mathrm {ref} })

Wobei:

U_{\mathrm {mpp} }

ist die Spannung auf dem MPP Betriebspunkt;

T_{\mathrm {ref} }

ist die Referenztemperatur;

T

ist die gemessene Temperatur;

u_{V_{\mathrm {mpp} }}

ist der Temperaturkoeffizient (von dem Hersteller des Moduls gegeben).

Technische Umsetzung

Software

In technischen Realisierungen dieses Verfahrens führt meist ein Mikrocontroller oder ein digitaler Signalprozessor eines der möglichen Verfahren durch. Dabei werden dem Prozessor die benötigten Messdaten von einem Analog-digital-Umsetzer zur Verfügung gestellt, womit dieser die nötigen Berechnungen durchführen kann und das Ergebnis mittels Pulsweitenmodulation an einen Gleichspannungswandler weitergibt.

Hardware

Da die Belastung der Solarzelle anhand der Belastungsspannung eingestellt wird, die Ausgangsspannung des Reglers jedoch nahezu konstant sein sollte, bedarf es eines Gleichspannungswandlers, um die Spannungsdifferenzen und somit die Belastung der Solarzelle einstellen zu können. Bei einem Photovoltaiksystem kann es durchaus vorkommen, dass sich der Spannungsbereich der optimalen Belastungsspannung der Solarzelle um die Spannung des zu ladenden Akkumulators bewegt. Somit kann die Eingangsspannung des Gleichspannungswandlers sowohl größer als auch kleiner sein als dessen Ausgangsspannung. Um dieser Anforderung gerecht zu werden, bedarf es einer Wandlertopologie, die diese Eigenschaft erfüllt, wie beispielsweise der Inverswandler, der Split-Pi-Wandler oder ein Wandler höherer Ordnung (Ćuk-Wandler, SEPIC-Wandler, Doppelinverter).

Literatur

Jitendra Prasad: Maximum Power Point tracker solar charge controller ( MPPT ): MPPT charge controller. LAP LAMBERT Academic Publishing, Saarbrücken 2012, ISBN 978-3-659-18508-3.

Weblinks

Commons: Maximum power point tracker – Sammlung von Bildern, Videos und Audiodateien

Projektbeschreibung eines MPPT auf Basis eines PIC-Mikrocontrollers (englisch) (MS Word; 5,1 MB)

Einzelnachweise

Photovoltaikforum.com: Schatten! Welche Wechselrichter aktivieren die Bypassdioden? In: Photovoltaikforum.com. Abgerufen am 18. Juli 2018.
SMA: Verschattungsmanagement. (PDF) SMA, abgerufen am 18. Juli 2018.
Video Schattenmanagement Kostal - YouTube. Abgerufen am 19. Juli 2018.
Optimization of Perturb and Observe Maximum Power Point Tracking Method. (PDF) Archiviert vom Original am 2. Dezember 2012; abgerufen am 24. September 2016.
Ratna Ika Putri, Sapto Wibowo, Muhamad Rifa’i: Maximum Power Point Tracking for Photovoltaic Using Incremental Conductance Method. In: Energy Procedia. Band 68, 1. April 2015, S. 22–30, doi:10.1016/j.egypro.2015.03.228 (ijera.com [PDF; abgerufen am 26. Dezember 2020]).
A MPPT approach based on temperature measurements applied in PV systems – IEEE Conference Publication. Abgerufen am 13. Oktober 2018 (amerikanisches Englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[:0-1] Photovoltaikforum.com: Schatten! Welche Wechselrichter aktivieren die Bypassdioden? In: Photovoltaikforum.com. Abgerufen am 18. Juli 2018.

[2] SMA: Verschattungsmanagement. (PDF) SMA, abgerufen am 18. Juli 2018.

[3] Video Schattenmanagement Kostal - YouTube. Abgerufen am 19. Juli 2018.

[4] Optimization of Perturb and Observe Maximum Power Point Tracking Method. (PDF) Archiviert vom Original am 2. Dezember 2012; abgerufen am 24. September 2016.

[5] Ratna Ika Putri, Sapto Wibowo, Muhamad Rifa’i: Maximum Power Point Tracking for Photovoltaic Using Incremental Conductance Method. In: Energy Procedia. Band 68, 1. April 2015, S. 22–30, doi:10.1016/j.egypro.2015.03.228 (ijera.com [PDF; abgerufen am 26. Dezember 2020]).

[6] A MPPT approach based on temperature measurements applied in PV systems – IEEE Conference Publication. Abgerufen am 13. Oktober 2018 (amerikanisches Englisch).