Doppelinverter

Als Doppelinverter bezeichnet man in der Elektronik eine elektronische Schaltung, die eine elektrische Gleichspannung in eine andere elektrische Gleichspannung wandeln kann. Der Betrag der Ausgangsspannung kann dabei sowohl kleiner als auch größer als die Höhe der ursprünglichen Eingangsspannung sein. Wie beim einfachen Inverswandler weist die Ausgangsspannung gegenüber der Eingangsspannung ein negatives Vorzeichen auf, die Ausgangsspannung ist invertiert. Der Doppelinverter wird somit zur Gruppe der invertierenden Gleichspannungswandler gezählt.

Aufbau

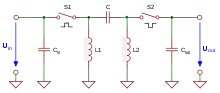
Prinzipschaltbild des Doppelinverters mit Schalter.

Wie der Ćuk-Wandler, der Zeta-Wandler und der SEPIC-Wandler zählt der Doppelinverter mit drei aktiven Energiespeichern, zwei Spulen und einem Kondensator, im Gegensatz zu einfachen Schaltwandlern wie dem Aufwärtswandler, dem Abwärtswandler und dem Inverswandler, zur Gruppe der Gleichspannungswandler höherer Ordnung. Wie bei jedem Gleichspannungswandler werden die Energiespeicher des Wandlers mit Hilfe von Halbleiterschaltern wie Transistoren und Dioden kontinuierlich zyklisch mit Energie geladen und entladen.

Im Gegensatz zum funktionell identischen Ćuk-Wandler befinden sich sowohl auf der Eingangsseite als auch auf der Ausgangsseite des Wandlers Halbleiterschalter. Der Stromfluss von Eingang und Ausgang wird somit ständig unterbrochen, daher ist sowohl der Ausgangsstrom als auch er Eingangsstrom diskontinuierlich. Dementsprechend müssen große Stützkondensatoren die damit verbundene Spannungswelligkeit ausgleichen. Der Doppelinverter besitzt in praktischen Realisierungen nur eine untergeordnete Bedeutung und kann durch die bessere Wandlertopologie des Ćuk-Wandlers ersetzt werden.

Mathematische Beschreibung und Funktion

Mögliche Realisierung des Doppelinverters.

Für die mathematische Beschreibung des Doppelinverters wird angenommen, dass alle Kondensatoren sehr groß sind und sich der Wandler bei konstantem Tasterverhältnis im eingeschwungenen Zustand befindet.

Der Strom in den Induktivitäten schwankt pro Schaltperiode um einen gewissen Wert Δi und ist somit im Mittel gleich null.

Die Spannung an einer Induktivität ergibt sich zu:

u_{\mathrm {L} }\left(t\right)=-L\cdot {\frac {\mathrm {d} i_{L}\left(t\right)}{\mathrm {d} t}}

Demnach müssen auch die Mittelwerte der Spannungen an den beiden Induktivitäten je Schaltperiode null ergeben.

Die Maschengleichung über die Induktivität L1 für die Sicht aus dem Eingangskreis ergibt sich zu:

-U_{\mathrm {in} }+U_{\mathrm {L1} }=0

U_{\mathrm {L1} }=U_{\mathrm {in} }

Die Maschengleichung über die Induktivität L1 für die Sicht aus dem Ausgangskreis ergibt sich zu:

-U_{\mathrm {L1} }+U_{\mathrm {C} }+U_{\mathrm {out} }=0

U_{\mathrm {L1} }=U_{\mathrm {c} }+U_{\mathrm {out} }

Berücksichtigt man nun das Tastverhältnis d, so liegt die jeweilige Spannung für die Dauer d (Eingangsseite, Transistor leitet) beziehungsweise für die Dauer 1-d (Ausgangsseite, Diode leitet) an. Dementsprechend ergibt die Addition beider Gleichungen unter Berücksichtigung des Tastverhältnisses die mittlere Spannung an der Induktivität, welche Null sein muss.

U_{\mathrm {L1} }=U_{\mathrm {in} }\cdot d+(1-d)\cdot (U_{\mathrm {C} }+U_{\mathrm {out} })=0

Die mittlere Spannung am Kondensator C ergibt sich somit zu:

U_{\mathrm {C} }=-U_{\mathrm {in} }\cdot {\dfrac {d}{1-d}}-U_{\mathrm {out} }

Die Spannung an der Induktivität L2 ergibt sich analog dazu zu:

U_{\mathrm {L2} }=d\cdot (U_{\mathrm {in} }-U_{\mathrm {C} })+(1-d)\cdot U_{\mathrm {out} }=0

Auch aus der zweiten Gleichung kann die Spannung am Kondensator C ausgedrückt werden:

U_{\mathrm {C} }=U_{\mathrm {out} }\cdot {\dfrac {1-d}{d}}+U_{\mathrm {in} }

Setzt man nun die beiden Gleichungen der Kondensatorspannungen gleich, so erhält man die Ausgangsspannung des Doppelinverters in Abhängigkeit von der Eingangsspannung und dem Pulsweitenverhältnis:

U_{\mathrm {out} }=-U_{\mathrm {in} }\cdot {\dfrac {d}{1-d}}

Schlussfolgerung

Setzt man nun die Gleichung für die Ausgangsspannung in die erste Gleichung für die Kondensatorspannung ein, so erhält man:

U_{\mathrm {C} }={\bigg (}-U_{\mathrm {in} }\cdot {\dfrac {d}{1-d}}{\bigg )}-{\bigg (}-U_{\mathrm {in} }\cdot {\dfrac {d}{1-d}}{\bigg )}

Wie man erkennen kann, ist die mittlere Spannung pro Schaltperiode am Kondensator null. Da der Kondensator als sehr groß angenommen wurde, kann weiters angenommen werden, dass sich auch die Spannung während einer Schaltperiode nur sehr Geringfügung ändern wird. Vereinfacht man diese Tatsache, ist die Spannung am Kondensator zu jeder Zeit null, wodurch der Kondensator weggelassen werden kann.

Es zeigt sich, dass nun die beiden Induktivitäten praktisch parallel geschaltet sind und so agieren, als ob es sich um eine einzelne Induktivität handeln würde. Dementsprechend kann der Doppelinverter als gewöhnlicher Inverswandler betrachtet werden.

Da der Doppelinverter somit die gleichen Eigenschaften wie der Inverswandler aufweist und praktisch keine Vorteile bietet, ist diese Wandlertopologie in der Praxis ohne Bedeutung und stellt daher mehr eine theoretische mögliche Wandlertopologie dar.

Siehe auch

Literatur

Franz Zach: Leistungselektronik: Ein Handbuch. 2 Bände 4. Auflage, Springer-Verlag, Wien, 2010, ISBN 978-3-211-89213-8

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.