Isogonal konjugierte Punkte

Als isogonal konjugierte Punkte bezeichnet man spezielle Punktepaare in der Ebene, bei denen die beiden Punkte in Bezug auf ein gegebenes Dreieck in einer speziellen Beziehung stehen.

Isogonal konjugierte Punkte P und Q

Definition

Die Definition isogonal konjugierter Punkte in Bezug auf ein Dreieck ergibt sich aus dem folgenden Satz:

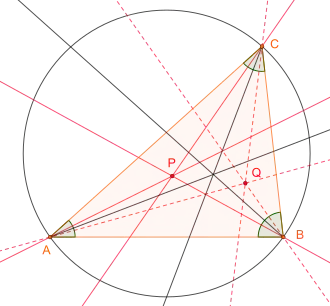
Es sei ABC ein Dreieck und P ein Punkt in Ebene, der nicht auf den Seiten oder dem Umkreis des Dreiecks liegt. Wir spiegeln die Geraden AP, BP und CP an den Winkelhalbierenden der Dreieckswinkel α, β bzw. γ. Dann schneiden sich die Spiegelbilder in einem neuen Punkt.

Dieser neue Punkt heißt der zu P isogonal konjugierte Punkt bezüglich des Dreiecks ABC (die Klausel „bezüglich des Dreiecks ABC“ lässt man meist weg, wenn keine Verwechslung zu befürchten ist, also wenn nur ein Dreieck im Spiel ist). Bezeichnen wir den zu P isogonal konjugierten Punkt mit Q, dann ist der zu Q isogonal konjugierte Punkt wiederum der Punkt P. Daher kann man die Punkte P und Q als zueinander isogonal konjugierte Punkte bezeichnen.

Äquivalente Definition

P sei ein Punkt des Dreiecks ABC, der nicht auf dessen Seiten oder Umkreis liegt. Spiegelt man P an den Seiten BC, AC und AB bzw. deren Verlängerungen, so entstehen die drei Bildpunkte P_a, P_b und P_c. Der Umkreismittelpunkt Q von Dreieck P_aP_bP_c heißt dann der zu P isogonal konjugierte Punkt bezüglich des Dreiecks ABC.

Erweiterung des Begriffs

Man kann die Konstruktion des isogonal konjugierten Punkts Q auch für Punkte P auf den Seiten des Dreiecks ABC, nicht jedoch für seine Eckpunkte durchführen. Die entstehenden Bildpunkte sind dann immer die gegenüberliegenden Ecken von Dreieck ABC. Damit ist die Abbildung, die jedem Punkt seinen isogonal konjugierten Punkt zuordnet, nicht mehr injektiv und man kann nicht mehr von zwei zueinander isogonal konjugierten Punkten P und Q sprechen.

Ebenso kann man die Definition auf Punkte auf dem Umkreis, die nicht die Eckpunkte sind, ausdehnen, wenn man zu der reellen Ebene deren projektiven Abschluss hinzunimmt beziehungsweise mit der projektiven reellen Ebene arbeitet. Liegt der Punkt P auf dem Umkreis, so sind die gespiegelten Verbindungsgeraden parallel und besitzen somit keinen Schnittpunkt. Da sich parallele Geraden aber im projektivem Abschluss der reellen Ebene, der sogenannten Ferngeraden, schneiden, liegen die isogonal konjugierten Punkte der Umkreispunkte dann auf dieser Ferngeraden.

Beispiele

Es gibt genau vier Punkte, die bezüglich des Dreiecks ABC zu sich selbst isogonal konjugiert sind: der Inkreismittelpunkt und die drei Ankreismittelpunkte.
Der Umkreismittelpunkt ist isogonal konjugiert zum Höhenschnittpunkt.
Der Schwerpunkt ist isogonal konjugiert zum Lemoinepunkt.
Der erste und der zweite Brocard-Punkt sind zueinander isogonal konjugiert.
Die Eckpunkte des Antimedialdreiecks und die entsprechenden Ecken des Tangentendreiecks sind paarweise isogonal konjugiert.

Eigenschaften

Hat ein Punkt die trilinearen Koordinaten $x:y:z$ , so sind die trilinearen Koordinaten des isogonal konjugierten Punktes gegeben durch ${\frac {1}{x}}:{\frac {1}{y}}:{\frac {1}{z}}$ .
Hat ein Punkt die baryzentrischen Koordinaten $x:y:z$ , so sind die baryzentrischen Koordinaten des isogonal konjugierten Punktes gegeben durch ${\frac {a^{2}}{x}}:{\frac {b^{2}}{y}}:{\frac {c^{2}}{z}}$ . Dabei stehen die Bezeichnungen $a$ , $b$ und $c$ für die Seitenlängen des Dreiecks.
Die Fußpunktdreiecke zweier isogonal konjugierter Punkte haben denselben Umkreis.
Bildet man die Punkte einer Geraden auf die zugehörigen isogonal konjugierten Punkte ab, so entsteht ein Kegelschnitt, der durch die Ecken des gegebenen Dreiecks geht. Der Typ dieses Kegelschnitts hängt davon ab, wie die gegebene Gerade und der Umkreis des Dreiecks liegen: Schneidet die Gerade den Umkreis, ergibt sich eine Hyperbel. Ist die Gerade eine Tangente des Umkreises, so entsteht eine Parabel. Falls die Gerade keine gemeinsamen Punkte mit dem Umkreis hat, erhält man eine Ellipse.

Siehe auch

Isotomisch konjugierte Punkte

Literatur

Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, S. 153–157, 213, 218, 224, 243 (Erstveröffentlichung 1929 bei der Houghton Mifflin Company (Boston) unter dem Titel Modern Geometry)
J. Clemow: A Note on Isogonal Conjugates. The Mathematical Gazette, Band 18, Nr. 231 (Dez., 1934), S. 289–293 (JSTOR)
David F. Barrow: A Theorem About Isogonal Conjugates. The American Mathematical Monthly, Band 20, Nr. 8 (Okt., 1913), S. 251–253 (JSTOR)

Weblinks

Commons: Isogonal Conjugates – Sammlung von Bildern, Videos und Audiodateien

Eric W. Weisstein: Isogonal konjugierte Punkte. In: MathWorld (englisch).
Paul Yiu: Isotomic and isogonal conjugates – Kapitel 12 eines Geometrieskripts (PDF, 10 seiten)
Navneel Singhal: Isotomic and isogonal conjugates (PDF, 12 Seiten)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.