Laplace-Ebene

Die Laplace-Ebene bezeichnet in der Himmelsmechanik die über lange Zeiten gemittelte Bahnebene eines Körpers (z. B. eines Planeten oder Satelliten), der sich auf einer Umlaufbahn um ein Zentralobjekt (beispielsweise die Sonne oder einen Planeten) bewegt.

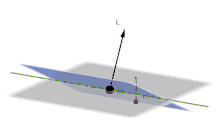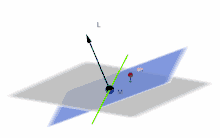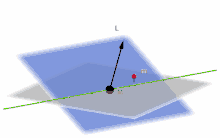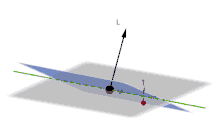
Illustration der Laplace-Ebene eines Himmelskörpers als zeitlich gemittelte Bahnebene
Grau: Laplace-Ebene
Blau: Momentane Bahnebene
M (schwarz): Zentralkörper
m (rot): Umlaufender Körper
L: Bahndrehimpuls-Vektor
Grün: Knotenlinie

Die Laplace-Ebenen der meisten großen Monde unseres Sonnensystems, insbesondere die der großen Gasplaneten, orientieren sich an der Äquatorebene des jeweiligen Zentralplaneten. Eine Ausnahme bildet der Erdmond, dessen Laplace-Ebene mit großer Genauigkeit in der Ekliptik liegt. Die Laplace-Ebenen künstlicher Satelliten im höheren Erdorbit und die einiger (überwiegend kleinerer) Monde anderer Planeten liegen zwischen der Bahnebene und der Äquatorebene ihres Zentralkörpers und müssen daher explizit berechnet werden.

Pierre-Simon Laplace hatte 1805 diese Bezugsebene als erster zur Beschreibung der Bahneigenschaften des Saturnmondes Iapetus eingeführt, des größten Mondes des Sonnensystems, bei dem diese Ebene deutlich sowohl von der Äquatorebene als auch von der Bahnebene des Planeten abweicht.[1][2]

Einleitung

Bewegt sich ein Körper um ein Zentralobjekt, so kann ihm zu jedem Zeitpunkt eine momentane Bahnebene zugeordnet werden. Dies ist die Ebene, in der sowohl der Abstandsvektor vom Zentralobjekt zum Körper als auch der Geschwindigkeitsvektor des sich bewegenden Körpers liegt. Der Bahndrehimpulsvektor des Körpers steht gerade senkrecht auf dieser Ebene. Unterliegt die Bewegung des Körpers keinem Drehmoment, so ändert sich der Bahndrehimpuls des Körpers nicht und die Bahnebene des Körpers ist entsprechend zeitlich konstant. Dies ist beispielsweise der Fall, wenn das Zentralobjekt exakt kugelsymmetrisch ist und keine äußeren Kräfte auf das System wirken.

In der Realität sind allerdings die Zentralobjekte weder exakt kugelsymmetrisch (die Planeten sind mehr oder weniger stark abgeplattet) noch ist die Bewegung frei von äußeren Kräften (durch die Sonne, andere Planeten etc.). Daher wirken auf die umlaufenden Körper Drehmomente, die zu einer Veränderung der Bahnebene führen, die in den meisten Fällen zwar gering im Laufe weniger Umläufe um das Zentralobjekt ist, aber im Laufe der Zeit zu einer Präzessionsbewegung des Bahndrehimpulses führen. Im Falle der Planeten-, Mond- und Satellitenbahnen kann man diesen Effekt über längere Zeiträume durch die Wirkung eines konstanten Drehmoments auf einen sich schnell bewegenden Kreisel modellieren. Die Bahnebene schwankt dann mit einer gewissen zeitlichen Periode um eine über lange Zeiten gemittelte Bahnebene (Laplace-Ebene). Der Neigungswinkel der momentanen Bahnebene gegen die Laplace-Ebene bleibt dabei näherungsweise konstant, nur die Lage der Ebenen zueinander ändert sich.

Forschungsgeschichte und der Saturnmond Iapetus

Bei der Analyse der Bahnen der großen Monde des Planeten Jupiter stellte der französische Mathematiker Laplace fest, dass sie über kurze Zeiträume (wenige Jahre), wie die Bahnen der Planeten, in einer Ebene verläuft. Über mittlere Zeiträume – oft einige Jahre bis Jahrzehnte – ist diese Bahnebene allerdings veränderlich: ein Effekt, der beim Erdmond seit der Antike bekannt ist, da sie eng mit dem jahreszeitlichen Auftreten der Sonnen- und Mondfinsternisse zusammenhängt. Laplace sah, dass die Bahnebene der Monde über lange Zeiträume eine kreiselartige Trudelbewegung vollzieht. Für den Erdmond ist diese Drehung der so genannten Mondknoten damals seit langer Zeit bekannt gewesen, wobei die Periode dieser Drehung 18,6 Jahre beträgt (Nutation). Betrachtet man anstelle der Bahnebene den Pol der Bahnebene, also den Punkt auf der Himmelssphäre, an dem eine gedachte Linie, die senkrecht auf der Bahnebene steht (die Normale), durch diese Sphäre sticht, so vollführt dieser Pol eine Kreisbewegung auf der Himmelssphäre. Beim Erdmond hat dieser Kreis einen Durchmesser von etwa 10° (die doppelte Bahnneigung des Mondes) und sein Mittelpunkt ist der Pol der Ekliptik (also der Erdbahnebene). Bei den Jupitermonden ist der Mittelpunkt dieser Kreise allerdings der „Himmelspol des Jupiter“, also der Punkt, an dem die Jupiterachse durch die Himmelssphäre sticht. Laplace stellte dazu die entsprechende Theorie dar, die diese Knotenbewegung auf die Abplattung des Jupiter und das dadurch ausgeübte Drehmoment zurückführt (und nicht das durch die Sonne ausgeübte Drehmoment, das beim Erdmond maßgeblich ist).[3]

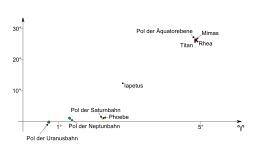
Lage der Laplace-Ebenen wichtiger Saturnmonde in Bezug auf die Rotations- und Bahnebene des Saturn. Die Pole der verschiedenen Ebenen sind im Diagramm auf die Ekliptik projiziert, so dass der Pol der Ekliptik im Ursprung liegt. Der Frühlingspunkt liegt dabei in Richtung der x-Achse. Ebenfalls dargestellt sind die Pole der Bahnebenen der äußeren Planeten.

Im Gegensatz zu den anderen damals bekannten Satelliten der Gasplaneten war mit der Entdeckung von Iapetus im Jahr 1671 schon frühzeitig ein Saturnmond bekannt, der seinen Zentralplaneten in recht großem Abstand (etwa 3,5 Mio. km) umkreist. Bei der Analyse der Bahn dieses Mondes stellte der französische Mathematiker Laplace fest, dass sie über kurze Zeiträume (wenige Jahre), wie die Bahn aller anderen Monde und Planeten, in einer Ebene verläuft. Über mittlere Zeiträume – in diesem Fall mehrere Jahrzehnte – ist die entsprechende Bahnebene wiederum veränderlich, wie dies vom Erdmond und den Jupitermonden ja bereits beobachtet worden war. Obwohl Iapetus 1805 erst 134 Jahre lang beobachtet worden war und die Beobachtungsdaten der Saturnmonde noch nicht an die Exaktheit der Daten für die Jupitermonde heranreichte, sah Laplace, dass die Bahnebene des Mondes über Zeiträume von einigen Jahrtausenden eine kreiselartige Trudelbewegung vollzieht. Bei Iapetus hat der entsprechende Kreis, den der Pol der Ebene beschreibt, einen Durchmesser von etwa 15°. Allerdings liegt in seinem Zentrum nicht der Pol der Saturnbahnebene und auch nicht der Pol der Äquatorebene des Saturn (also der Durchstichpunkt der Drehachse des Planeten durch die Himmelssphäre).[1] Stattdessen liegt der Mittelpunkt, wie man im nebenstehenden Diagramm sehen kann, etwa zwischen dem Pol der Saturnbahnebene und dem Pol der Äquatorebene des Saturn. Alle anderen damals bekannten Monde (dies waren die vier Galileischen Monde, sechs weitere Saturnmonde, sowie zwei Uranusmonde) haben Bahnen, die sich kaum mehr als ein Grad gegen die Äquatorebene des Zentralplaneten neigen. Bei Messungen hoher Präzision stellt man fest, dass die Bahnpole dieser Monde ebenfalls kreisförmige Bewegungen vollführen, und zwar um den Pol der Äquatorebene des Planeten.

Der Mittelpunkt des Kreises, auf dem sich der Bahnpol eines Mondes bewegt, ist der Pol der über lange Zeiträume gemittelten Bahnebene, die selbst zeitlich unveränderlich ist: die Laplace-Ebene. Bei den planetennahen Monden der massereichen und sonnenfernen Gasplaneten fällt diese mit der Äquatorebene zusammen. Beim Erdmond fällt diese, ebenso wie beim 1888 entdeckten äußeren Saturnmond Phoebe (Planetenabstand etwa 13 Mio. km), sehr genau mit dem Pol der Bahnebene des jeweiligen Planeten zusammen. Der Fall des Mondes Iapetus zeigt, dass es allerdings eine Zone mittleren Abstandes vom Planeten gibt, in der die Laplace-Ebene eine Zwischenform annimmt. Heute, im 21. Jahrhundert, sind hunderte Planetenmonde bekannt und künstliche Satelliten in Planetenorbits gestartet worden, deren exakte Bahndynamik den Spezialfall des Iapetus verallgemeinern. Diese Tatsache verlangt unmittelbar nach einer Klärung der Frage, wie die genaue Dynamik der Bahnebenen im allgemeinen Fall aussieht.

Himmelsmechanische Erklärung

Der Idealfall eines kleinen Körpers, der sich um ein kugelförmiges Zentralobjekt bewegt, wird durch das Kepler’sche Zweikörperproblem oder das Einzentrenproblem beschrieben. Da das Gravitationsfeld des kugelförmigen Zentralobjekts radialsymmetrisch ist, wirkt kein Drehmoment auf den umlaufenden Körper und der Bahndrehimpuls des Körpers ist in diesem Fall zeitlich konstant. Dies bedingt einerseits die Gültigkeit des zweiten Kepler’schen Gesetzes und andererseits, dass die Bewegung des kleinen Körpers in einer zeitlich unveränderlichen Ebene, der Bahnebene, erfolgt.

A – Himmelskörper
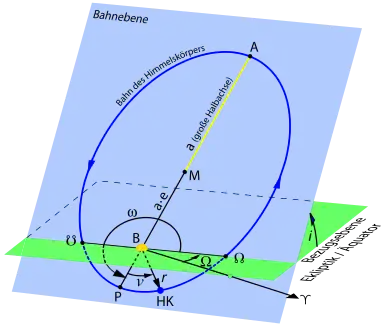
B – Zentralobjekt
Grün – Referenzebene (Laplaceebene)
Blau – Orbitalebene (Bahnebene)
i – Inklination
Ω – Länge des aufsteigenden Knotens

Die Bahnen realer Körper im Orbit um ein Zentralobjekt, wie zum Beispiel Planeten im Umlauf um die Sonne, Monde im Umlauf um ihren Planeten, oder künstliche Satelliten, können nur annäherungsweise als Zweikörperproblem behandelt werden. Abweichungen von der Kugelgestalt des Zentralobjekts und die Anwesenheit anderer massiver Körper außerhalb des Systems führen zu einem gestörten Zweikörpersystem. Solch ein gestörtes System lässt sich über kurze Zeiträume zwar weiterhin durch die Bahnelemente einer Keplerellipse beschrieben, die Störungen führen aber zu einer zeitlichen Veränderung der Bahnelemente. Insbesondere führt ein Drehmoment, das auf den umlaufenden Körper wirkt, zur zeitlichen Veränderung der Bahnebene, die in der Himmelsmechanik im Allgemeinen durch die Bahnneigung (Inklination) i und den Positionswinkel (Argument) des aufsteigenden Knotens Ω in Bezug auf eine unveränderliche Referenzebene angegeben wird.

Die Natur der auftretenden Drehmomente T ist oft derart, dass diese recht klein im Verhältnis zum Bahndrehimpuls L sind, d. h., der Drehimpuls ändert sich sehr wenig während eines Umlaufs des Körpers um das Zentralobjekt, in Formeln: $T/L\ll \omega$ , wobei ω die Kreisfrequenz des Körpers beim Umlauf ist. In diesem Fall kann man den Körper als schnellen Kreisel betrachten, dessen Rotationsachse in Richtung des Bahndrehimpulses zeigt. Durch das Drehmoment ändert die Rotationsachse ihre Richtung dergestalt, dass sie kurzperiodisch um eine mittlere Rotationsachse wandert, die ihrerseits langperiodisch um einen Präzessionspol wandert. Die Ebene senkrecht zur Richtung des Präzessionspols kann langzeitlich als mittlere Bahnebene betrachtet werden und wird als Laplace-Ebene bezeichnet.

Planeten, Monde und Satelliten bewegen sich oft auf Ellipsen relativ geringer Exzentrizität um ihren Zentralkörper, und die Drehmomente, die auf den Körper wirken, sind meist von den in den drei folgenden Absätzen beschriebenen Mechanismen bewirkt.

Abweichungen des Zentralkörpers von der Kugelgestalt

Solange beide Körper in einem Zweikörpersystem exakt kugelsymmetrischen Aufbau besitzen, ist das Gravitationsfeld im resultierenden äquivalenten Einzentrenproblem exakt radialsymmetrisch und es wirkt kein Drehmoment zwischen den umlaufenden Körpern. Abweichungen von der Kugelgestalt führen jedoch zum Auftreten eines Drehmomentes und damit zur zeitlichen Veränderung der Bahnebene. Im himmelsmechanischen Kontext ist die dominante Quelle dieses Drehmoments das Quadrupolmoment $J_{2}$ des Zentralkörpers, das sich zum großen Teil durch die Abplattung längs der Rotationsachse des Körpers ergibt. Das Drehmoment, das sich gemittelt über eine Umlaufperiode ergibt, steht senkrecht auf der Rotationsachse des Zentralkörpers und senkrecht auf dem momentanen Bahndrehimpuls des umlaufenden Körpers. Dadurch ändert sich der Betrag des Drehimpulses nicht, sondern nur die Richtung präzediert um die Rotationsachse des Zentralkörpers. Die Drehimpulserhaltung bedingt dabei im Übrigen eine Rückwirkung auf den Eigendrehimpuls des Zentralkörpers, der dadurch, im Allgemeinen aber sehr viel langsamer, um den Präzessionspol des umlaufenden Körpers präzediert. Diese Wirkung des Erdmondes ist zum Beispiel einer der Hauptgründe für die lunisolare Präzession der Erdachse.

Weist man der Rotationsachse des Zentralkörpers einen Richtungsvektor ${\vec {n}}$ zu, der unter Vernachlässigung der gerade beschriebenen Rückwirkung über nicht allzu lange Zeiträume als konstant angesehen werden kann, so zeigt eine genaue Rechnung, dass die Winkelgeschwindigkeit ${\vec {\omega }}$ der Umlaufbewegung[A 1] um die Rotationsachse ${\vec {n}}$ präzediert.[4] [A 2] Dabei ändert sich das Skalarprodukt $\langle {\vec {\omega }},{\vec {n}}\rangle =:\omega \cos i$ zeitlich nicht, d. h., die Bahnneigung i gegenüber der Äquatorebene des Zentralobjekts, die somit die Laplace-Ebene ist, ändert sich nicht. Das Knotenargument der Umlaufbahn wandert dann mit einer Winkelgeschwindigkeit von

{\dot {\Omega }}=-{\frac {3J_{2}R^{2}\omega }{2a^{2}}}\cos i,

mit dem Radius R des Zentralkörpers und der großen Halbachse a der Umlaufbahn.

Für Planeten, die man im Allgemeinen als Rotationsellipsoide annehmen kann, lässt sich das Quadrupolmoment durch $J_{2}=I\cdot f/(MR^{2})$ aus dem Trägheitsmoment I und der Abplattung f berechnen.[A 3] Zum Beispiel gilt für die Erde f ≈ 1/298 und I ≈ 0,33 M R² also J₂ ≈ 0,0011 in guter Übereinstimmung mit dem genaueren Wert[5] J₂ = 0,001082.

Setzt man dies in die Formel oben ein und berechnet man die Periode der Knotendrehung für einen Satelliten auf erdnahem, fast äquatorialem Orbit, so erhält man eine Knotenwanderung von etwa 10° pro Tag entgegen der Umlaufrichtung des Satelliten, d. h., der Knoten läuft in etwa 36 Tagen einmal um den Äquator der Erde.

Für Jupiter findet man[6] J₂ ≈ 0,0147 und einen Radius von R ≈ 71.500 km. Der Mond Io kreist in einem Abstand von etwa a ≈ 421.000 km um den Planeten und der Bahnknoten wandert entsprechend um etwa 47° pro Jahr und braucht rund 7,66 Jahre für eine volle Umdrehung, in guter Übereinstimmung mit den gemessenen 7,42 Jahren.[7] Die ohnehin geringe Bahnneigung gegenüber Jupiters Äquatorebene von 0,05° bleibt in guter Übereinstimmung mit dem hier vorgestellten Modell konstant, eine Tatsache, die weder für künstliche Satelliten im Erdorbit noch für den Erdmond gilt.

Für den Erdmond schwankt die Neigung gegenüber dem Erdäquator mit einer Periode von 18,6 Jahren zwischen 18° und 28,5°. Die Abplattung der Erde würde allerdings nur eine Drehung der Knoten von etwa 2,1° pro Jahrtausend bei gleichbleibender Neigung verursachen, sodass die Dynamik der Mondknoten eine andere Ursache besitzen muss; sie wird nun vorgestellt.

Äußere Störungen am Beispiel des Erdmondes

Illustration zur Wanderung des Bahnknotens einer durch einen äußeren Körper gestörten Umlaufbahn. Es bezeichnet: E: Zentralobjekt (z. B. Erde) M: Umlaufender Körper (z. B. Mond) O: Umlaufbahn von M (der oberhalb der Laplace-Ebene liegende Teil ist dicker) R: Richtung der vektoriellen Winkelgeschwindigkeit P: Präzessionskegel von R S: Störkörper (z. B. Sonne) B: Relative Bahn von S (z. B. Ekliptik) L: Laplace-Ebene (z. B. Ekliptik-Ebenen)

Wird ein Zweikörpersystem in eine Umgebung eingebracht, in der andere Objekte mit den beiden Körpern wechselwirken, so lässt sich unter gewissen Bedingungen die Bewegung der beiden Körper störungstheoretisch behandeln. Man geht bei diesem Ansatz davon aus, dass sich das Zweikörpersystem über kurze Zeiten weiterhin in der Form beschrieben lässt, die aus dem ungestörten Problem bekannt ist. Über mittlere und längere Zeiträume werden sich jedoch eigentlich konstante Bahnparameter dynamisch entwickeln. In diesem Abschnitt soll ein gewisser Spezialfall der Störung einer Keplerellipse beschrieben werden, wobei das Interesse wiederum bei den Bahnelementen Inklination i und Argument des aufsteigenden Knotens Ω liegt. Man geht zu diesem Zweck von den Annahmen aus, dass sich der umlaufende Körper wieder als schneller Kreisel beschreiben lässt und dass sich die störenden Körper schnell bewegen im Verhältnis zur Änderungsrate der Bahnelemente. Als Beispiel für ein solches Modell sei der Erdmond gewählt, der sich mit etwa der 13-fachen Winkelgeschwindigkeit um die Erde bewegt, mit der sich der Hauptstörkörper, nämlich die Sonne, relativ zum Erde-Mond-System bewegt. Die Änderung des relevanten Bahnelements Ω vollzieht sich mit nochmal etwa 18-fach kleinerer Winkelgeschwindigkeit.

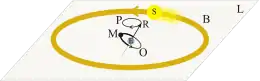
Man erhält in solchen Fällen ein akzeptables Resultat, wenn man ein solches System als schnellen Kreisel betrachtet, auf den eine Kraft wirkt, die von einer Masseverteilung ausgeht, die aus einer zeitlichen Mittelung der Störmassen über ihre Bahnen relativ zum Zweikörpersystem hervorgeht. Handelt es sich dabei um einen einzelnen dominanten Störkörper, der sich relativ zum System mit konstantem Abstand und konstanter Geschwindigkeit bewegt, kann man also von einem eindimensionalen Massering mit entsprechender Masse M und Radius R ausgehen. Das Drehmoment, das dieser Massering auf den umlaufenden Körper bewirkt, erzeugt eine Änderung der Richtung des Drehimpulses und damit der Bahnebene.[A 4]

Der aufsteigende Knoten der Umlaufbahn wandert daher mit einer Winkelgeschwindigkeit von[4][8]

{\dot {\Omega }}=-{\frac {3GM}{4r^{3}\omega }}\cos i,

wobei M die Masse des Störkörpers und r sein Abstand zum System ist. i bezeichnet nun die Bahnneigung ( $\cos i=\langle {\vec {\omega }},{\vec {n}}\rangle /\omega$ ) gegenüber der Bahnebene des Störkörpers, die hier die Laplace-Ebene ist und deren Normale ${\vec {n}}$ senkrecht auf ihr steht. Wie im vorigen Abschnitt gilt auch hier, dass Betrag der Winkelgeschwindigkeit und Bahnneigung zeitlich konstant sind.

Wenn der Störkörper, wie im Falle des Erde-Mond-Systems, der Zentralkörper eines größeren Gesamtsystems (z. B. Sonnensystem) ist, kann in der obigen Formel die Masse und der Abstand dieses Körpers durch das dritte Kepler’sche Gesetz eliminiert werden und man erhält

{\dot {\Omega }}=-{\frac {3\omega _{0}^{2}}{4\omega }}\cos i,

wobei ω₀ hier die Winkelgeschwindigkeit des Störkörpers (Sonne) ist. Für den Fall des Erdmondes kann man nun direkt ablesen, dass (unter Vernachlässigung der Bahnneigung) die Mondknoten mit einer Winkelgeschwindigkeit wandern, die etwa 4/3 · ω/ω₀ ≈ 1,33 · 13,4 ≈ 17,8-mal langsamer ist als die relative Winkelgeschwindigkeit der Sonne – in anderen Worten: Die Knoten drehen sich alle 17,8 Jahre um volle 360°. Der beobachtete Wert von 18,6 Jahren ergibt sich erst durch genauere Berechnung der Mondbahn.[8] Die Bahnneigung des Mondes ist bei dieser Wanderung der Knoten, abgesehen von kurzperiodischen Schwankungen, gegenüber der Ekliptik (Laplace-Ebene) konstant etwa 5°. Setzt man allerdings zum Beispiel die Daten des Jupitermondes Io ein, so erhält man, dass die Knoten fast 40.000 Jahre für einen vollen Umlauf bräuchten – ein Effekt, der um fast vier Zehnerpotenzen kleiner ist als der durch die Abplattung des Zentralplaneten hervorgerufene.

Kombination beider Fälle

In vielen himmelsmechanisch relevanten Fällen sind die beiden eben beschriebenen Effekte von vergleichbarer Größenordnung. Sind in einem solchen Fall die Rotationsachse des Zentralkörpers und der Bahndrehimpuls des äußeren Störkörpers parallel, so addieren sich beide Effekte und man erhält:[A 5]

{\dot {\Omega }}=-\left({\frac {3GM}{4r^{3}\omega }}+{\frac {3J_{2}R^{2}\omega }{2a^{2}}}\right)\cos i.

Die Präzession erfolgt dabei wiederum kreisförmig um die gemeinsame Richtung von Rotationsachse des Zentralkörpers und Bahndrehimpuls des Störkörpers. Entsprechendes gilt auch für die Überlagerung mehrerer äußerer Störungen, die alle in derselben Ebene auftreten. Während diese Annahme für äußere Störungen oft gerechtfertigt ist – Sonne und Mond stören Satelliten im Erdorbit beide etwa in der Ekliptik, die kleinen äußeren Jupitermonde werden durch Sonne und Saturn ebenfalls etwa in der Ekliptik gestört etc. – weichen die Äquatorebenen der Planeten oft wesentlich von der Ekliptikebene ab. Der Erdäquator ist zum Beispiel 23,5°, der Saturnäquator 26,8° gegen die Ekliptik geneigt und bei Uranus stehen die Ebenen fast senkrecht aufeinander. Dadurch können sowohl künstliche Satelliten im Erdorbit, als auch der große Saturnmond Iapetus, für die beide Effekte von vergleichbarer Größenordnung sind, nicht durch die obige Gleichung beschrieben werden können. Stattdessen führt die Überlagerung i. Allg. zu einer komplizierten Dynamik mit einer Präzession und einem Pol, der zwischen Rotationsachse des Zentralkörpers und Bahndrehimpuls des Störkörpers liegt.[A 6] Dies führt weiterhin dazu, dass die Bahnneigung auch in Bezug auf die Laplace-Ebene nicht konstant ist, sondern periodisch zwischen einem minimalen und einem maximalen Wert schwankt.[A 7] Wie stark diese Schwankung der Bahnneigung ist, hängt neben den Größen der beiden Drehmomente wesentlich auch vom Winkel zwischen diesen beiden ab. Besonders gravierend ist dieser Effekt daher beim Planeten Uranus, dessen Äquatorebene fast senkrecht auf seiner Bahnebene steht.[A 8]

Ein Beispiel an den Jupitermonden

Lage der Laplace-Ebenen wichtiger Jupitermonde in Bezug auf die Rotations- und Bahnebene des Jupiter. Die Pole der verschiedenen Ebenen sind im Diagramm auf die Ekliptik projiziert, so dass der Pol der Ekliptik im Ursprung liegt. Der Frühlingspunkt liegt dabei in Richtung der x-Achse. Ebenfalls dargestellt sind die Pole der Bahnebenen der äußeren Planeten.

Im System der zahlreichen Jupitermonde können die verschiedenen oben beschriebenen Effekte beispielhaft nachvollzogen werden.[7] Wie man in nebenstehender Grafik erkennen kann, ordnen sich die Pole der Laplace-Ebenen der inneren Monde alle in der Nähe der Rotationsachse des Zentralplaneten unten links im Diagramm an. Die Laplace-Ebene von Kallisto (IV), die einen Abstand von knapp 1,9 Mio. km zum Jupiter hat, ist dabei schon deutlich in die Richtung der Bahnebene des Jupiters und damit der Ebene, in der die Sonne als Störkörper wirkt, gezogen.

Der nächstäußere Mond Themisto (XVIII), der etwa 7,5 Mio. km Abstand vom Jupiter hat, hat eine Laplace-Ebene, die schon vornehmlich von der Bahnebene und kaum noch von der Äquatorebene beeinflusst wird (oben rechts im Diagramm). In diesem Bereich ordnen sich auch alle anderen äußeren Monde des Jupiters an. Allerdings wird unmittelbar deutlich, dass allein das Wechselspiel von Äquator- und Bahnebene des Jupiters nicht zur Erklärung der Laplace-Ebenen dieser Monde ausreicht. Diese liegen vielmehr in einer großen Wolke um die Bahnebene des Jupiters. Grund dafür sind die Drehmomente, die in Richtung der Bahnpole der drei weiter außen liegenden großen Planeten Saturn, Uranus und Neptun wirken, die daher ebenfalls eingezeichnet sind. Dieser Effekt lässt sich deutlich im ersten Diagramm dieses Artikels für den Saturnmond Iapetus erkennen, dessen Laplace-Ebene deutlich aus der Verbindungslinie zwischen Rotationsachse und Bahnpol in Richtung der Bahnpole der weiter außen gelegenen Planeten gezogen wird.

Ein besonders extremer Fall ist die Laplace-Ebene von Ananke (XII), die fast drei Grad über die Bahnebene des Jupiters hinaus geneigt ist und auch jenseits der Bahnebene des Saturns im Diagramm liegt. Unter allen bekannten Jupitermonden stellt Ananke damit einen krassen Ausreißer dar, der nur durch speziell hier auftretende Bahnstörungen erklärt werden kann.

Invariable Ebene

Die Laplace - Ebene ist nicht zu verwechseln mit der invariablen Ebene. Diese entsteht durch den Gesamtdrehimpuls eines Systems (Planet - Monde - System oder Sonne - Planeten - System) und erstreckt sich im Gegensatz zur Laplace - Ebene (Animation oben rechts im Artikel) durch deren Baryzentrum (Massen - Schwerpunkt). Der Vektor des Gesamtdrehimpulses steht senkrecht auf der invariablen Ebene. Der Gesamtdrehimpuls beinhaltet die Bewegungen des umlaufenden Körpers um das Zentralobjekt, nicht jedoch die Eigenrotationen, wie in der Laplace - Ebene. Die Darstellung des Gesamtdrehimpulses lautet $L=R^{2}M{\dot {\theta }}$ , mit $R$ als dem Abstand des Planeten von Baryzentrum, mit $M$ als der Planetenmasse und ${\dot {\theta }}$ als der Winkelgeschwindigkeit des Planeten um das Baryzentrum. Weil auf das Sonnensystem selbst keine (bekannte) äußeren Kräfte einwirken, die eine Präzession des Gesamtdrehimpulses zur Folge hätten, besitzt das Sonnensystem keine Laplace - Ebene. Laplace - Ebenen kommen nur bei Planet - Monde - Systemen vor.

Anmerkungen

Die Richtung der vektoriellen Winkelgeschwindigkeit ist parallel zum Bahndrehimpuls.
Setzt man eine Bahn geringer Exzentrizität voraus, führt genauere Rechnung auf eine Änderung der vektoriellen mittleren Winkelgeschwindigkeit des umlaufenden Körpers von
${\dot {\vec {\omega }}}=-{\frac {3J_{2}R^{2}}{2a^{2}}}\langle {\vec {\omega }},{\vec {n}}\rangle {\vec {n}}\times {\vec {\omega }},$
wobei $J_{2}$ das dimensionslose Quadrupolmoment, ${\vec {n}}$ der Richtungsvektor der Rotationsachse des Zentralobjekts, R dessen Radius und a die große Halbachse der Umlaufbahn bezeichnet (die spitzen Klammern stellen das Skalarprodukt dar). Durch das Vektorprodukt steht die Änderung der Winkelgeschwindigkeit senkrecht auf der Winkelgeschwindigkeit, so dass diese ihren Betrag zeitlich nicht ändert.
Das Quadrupolmoment eines homogenen Rotationsellipsoids beträgt $J_{2}={\frac {2}{5}}f,$ wobei f die Abplattung des Körpers ist. Reale Planeten sind hingegen nicht homogen; ihre Dichte nimmt mit wachsender Entfernung vom Mittelpunkt ab. Nimmt man an, dass der Körper aus Schichten gleicher Dichte aufgebaut ist, ist das Quadrupolmoment durch $J_{2}={\frac {I}{MR^{2}}}f$ gegeben, wobei I das Trägheitsmoment bezeichnet.
Das Drehmoment, das dieser Massering auf den umlaufenden Körper bewirkt, erzeugt eine Änderung der vektoriellen mittleren Winkelgeschwindigkeit des umlaufenden Körpers von:
${\dot {\vec {\omega }}}=-{\frac {3GM}{4r^{3}\omega ^{2}}}\langle {\vec {\omega }},{\vec {n}}\rangle {\vec {n}}\times {\vec {\omega }},$
wobei M die Masse des Störkörpers, ${\vec {n}}$ der Richtungsvektor der Winkelgeschwindigkeit des Störkörpers und r sein Abstand zum System ist.
Die entsprechende Differentialgleichung für die Winkelgeschwindigkeit lautet
${\dot {\vec {\omega }}}=-(A+B)\langle {\vec {\omega }},{\vec {n}}\rangle {\vec {n}}\times {\vec {\omega }}$
mit $A:=3J_{2}R^{2}/(2a^{2})$ und $B:=3GM/(4r^{3}\omega ^{2})$ .
Die Differentialgleichung nimmt die Form
${\dot {\vec {\omega }}}=-\left(A\langle {\vec {\omega }},{\vec {n}}_{z}\rangle {\vec {n}}_{z}+B\langle {\vec {\omega }},{\vec {n}}_{s}\rangle {\vec {n}}_{s}\right)\times {\vec {\omega }}$
an. ${\vec {n}}_{z}$ bezeichnet hierbei den Richtungsvektor der Rotationsachse des Zentralobjekts, ${\vec {n}}_{s}$ den Richtungsvektor der Winkelgeschwindigkeit des Störkörpers. Man sieht dieser Differentialgleichung an, dass der Betrag der Winkelgeschwindigkeit weiterhin konstant ist, da die Änderung der Winkelgeschwindigkeit ${\dot {\vec {\omega }}}$ immer senkrecht auf der Winkelgeschwindigkeit selbst steht (wiederum bedingt durch das Kreuzprodukt in der Differentialgleichung). Dadurch ist auch die Größe $B$ weiterhin konstant. Allerdings ist der Winkel der Bahnebene nun weder zur Rotationsachse des Zentralkörpers ${\vec {n}}_{z}$ noch zur Richtung der Winkelgeschwindigkeit des Störkörpers ${\vec {n}}_{s}$ konstant. Die Winkelgeschwindigkeit wandert stattdessen um einen Präzessionspol, der zwischen ${\vec {n}}_{z}$ und ${\vec {n}}_{s}$ liegt. Die Präzession um diesen Pol ist auch nicht mehr kreisförmig, sondern ellipsenförmig (genauer gesagt, handelt es sich bei der Kurve um eine auf eine Kugel projizierte Ellipse).
Betrachtet man die obige DGL genauer, sieht man, dass die Gleichung, da A und B konstant sind, quadratisch in ${\vec {\omega }}$ ist. Man kann die DGL als
${\dot {\vec {\omega }}}={\vec {\omega }}\times (M{\vec {\omega }})$
schreiben, wobei die Matrix
$M:=A|{\vec {n}}_{z}\rangle \langle {\vec {n}}_{z}|+B|{\vec {n}}_{s}\rangle \langle {\vec {n}}_{s}|$ (Bra-Ket-Schreibweise),
Rang 2 hat. Die beiden Eigenvektoren der Matrix sind Linearkombinationen der Richtungsvektoren ${\vec {n}}_{z}$ und ${\vec {n}}_{s}$ . Der eine Eigenvektor gibt die Richtung der Normalen zur Laplace-Ebene an, der andere die Richtung der großen Halbachse der ellipsenförmigen Kurve, die die vektorielle Winkelgeschwindigkeit um diesen Pol beschreibt.
Vernachlässigt man diesen Effekt, kommt man zu einer Näherung obiger Differentialgleichung für kleine Winkel zwischen den Ebenen:
${\dot {\vec {\omega }}}=-(A+B)\langle {\vec {\omega }},{\vec {n}}_{L}\rangle {\vec {n}}_{L}\times {\vec {\omega }},$
wobei ${\vec {n}}_{L}:=(A{\vec {n}}_{z}+B{\vec {n}}_{S})/(A+B)$ die Normale auf der Laplace-Ebene ist, die also gerade das gewichtete Mittel aus den Normalen auf Äquator- und Störbahnebene ist.

Einzelnachweise

Pierre-Simon Laplace: Mécanique céleste. (Englische Übersetzung). Band 4. Little & Brown, Boston 1829, Kap. 17, S. 315 ff. (englisch, archive.org – französisch: Traité de Mécanique céleste. 1805. Übersetzt von Nathaniel Bowditch).
R. R. Allan, G. E. Cook: The Long-Period Motion of the Plane of a Distant Circular Orbit, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 280, No. 1380 (Jul. 7, 1964), pp. 97–109
S. Laplace, Kap. IV, S. 62ff.
Satellitenbahnen Projekt TU-München (Memento des Originals vom 30. September 2007 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2
NASA Earth Fact Sheet
NASA Jupiter Fact Sheet (Memento des Originals vom 5. Oktober 2011 auf WebCite) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2
Planetary Satellite Mean Orbital Parameters vom JPL
M. Schneider: Himmelsmechanik, Kap. 26, Bd. 2, BI Wiss. Verlag, Mannheim (1993), S. 542--550

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[omega-4] Die Richtung der vektoriellen Winkelgeschwindigkeit ist parallel zum Bahndrehimpuls.

[oblat-6] Setzt man eine Bahn geringer Exzentrizität voraus, führt genauere Rechnung auf eine Änderung der vektoriellen mittleren Winkelgeschwindigkeit des umlaufenden Körpers von
${\dot {\vec {\omega }}}=-{\frac {3J_{2}R^{2}}{2a^{2}}}\langle {\vec {\omega }},{\vec {n}}\rangle {\vec {n}}\times {\vec {\omega }},$
wobei $J_{2}$ das dimensionslose Quadrupolmoment, ${\vec {n}}$ der Richtungsvektor der Rotationsachse des Zentralobjekts, R dessen Radius und a die große Halbachse der Umlaufbahn bezeichnet (die spitzen Klammern stellen das Skalarprodukt dar). Durch das Vektorprodukt steht die Änderung der Winkelgeschwindigkeit senkrecht auf der Winkelgeschwindigkeit, so dass diese ihren Betrag zeitlich nicht ändert.

[quadrupol-7] Das Quadrupolmoment eines homogenen Rotationsellipsoids beträgt $J_{2}={\frac {2}{5}}f,$ wobei f die Abplattung des Körpers ist. Reale Planeten sind hingegen nicht homogen; ihre Dichte nimmt mit wachsender Entfernung vom Mittelpunkt ab. Nimmt man an, dass der Körper aus Schichten gleicher Dichte aufgebaut ist, ist das Quadrupolmoment durch $J_{2}={\frac {I}{MR^{2}}}f$ gegeben, wobei I das Trägheitsmoment bezeichnet.

[stoer-11] Das Drehmoment, das dieser Massering auf den umlaufenden Körper bewirkt, erzeugt eine Änderung der vektoriellen mittleren Winkelgeschwindigkeit des umlaufenden Körpers von:
${\dot {\vec {\omega }}}=-{\frac {3GM}{4r^{3}\omega ^{2}}}\langle {\vec {\omega }},{\vec {n}}\rangle {\vec {n}}\times {\vec {\omega }},$
wobei M die Masse des Störkörpers, ${\vec {n}}$ der Richtungsvektor der Winkelgeschwindigkeit des Störkörpers und r sein Abstand zum System ist.

[kombination-13] Die entsprechende Differentialgleichung für die Winkelgeschwindigkeit lautet
${\dot {\vec {\omega }}}=-(A+B)\langle {\vec {\omega }},{\vec {n}}\rangle {\vec {n}}\times {\vec {\omega }}$
mit $A:=3J_{2}R^{2}/(2a^{2})$ und $B:=3GM/(4r^{3}\omega ^{2})$ .

[DGLkombi1-14] Die Differentialgleichung nimmt die Form
${\dot {\vec {\omega }}}=-\left(A\langle {\vec {\omega }},{\vec {n}}_{z}\rangle {\vec {n}}_{z}+B\langle {\vec {\omega }},{\vec {n}}_{s}\rangle {\vec {n}}_{s}\right)\times {\vec {\omega }}$
an. ${\vec {n}}_{z}$ bezeichnet hierbei den Richtungsvektor der Rotationsachse des Zentralobjekts, ${\vec {n}}_{s}$ den Richtungsvektor der Winkelgeschwindigkeit des Störkörpers. Man sieht dieser Differentialgleichung an, dass der Betrag der Winkelgeschwindigkeit weiterhin konstant ist, da die Änderung der Winkelgeschwindigkeit ${\dot {\vec {\omega }}}$ immer senkrecht auf der Winkelgeschwindigkeit selbst steht (wiederum bedingt durch das Kreuzprodukt in der Differentialgleichung). Dadurch ist auch die Größe $B$ weiterhin konstant. Allerdings ist der Winkel der Bahnebene nun weder zur Rotationsachse des Zentralkörpers ${\vec {n}}_{z}$ noch zur Richtung der Winkelgeschwindigkeit des Störkörpers ${\vec {n}}_{s}$ konstant. Die Winkelgeschwindigkeit wandert stattdessen um einen Präzessionspol, der zwischen ${\vec {n}}_{z}$ und ${\vec {n}}_{s}$ liegt. Die Präzession um diesen Pol ist auch nicht mehr kreisförmig, sondern ellipsenförmig (genauer gesagt, handelt es sich bei der Kurve um eine auf eine Kugel projizierte Ellipse).

[eigenwerte-15] Betrachtet man die obige DGL genauer, sieht man, dass die Gleichung, da A und B konstant sind, quadratisch in ${\vec {\omega }}$ ist. Man kann die DGL als
${\dot {\vec {\omega }}}={\vec {\omega }}\times (M{\vec {\omega }})$
schreiben, wobei die Matrix
$M:=A|{\vec {n}}_{z}\rangle \langle {\vec {n}}_{z}|+B|{\vec {n}}_{s}\rangle \langle {\vec {n}}_{s}|$ (Bra-Ket-Schreibweise),
Rang 2 hat. Die beiden Eigenvektoren der Matrix sind Linearkombinationen der Richtungsvektoren ${\vec {n}}_{z}$ und ${\vec {n}}_{s}$ . Der eine Eigenvektor gibt die Richtung der Normalen zur Laplace-Ebene an, der andere die Richtung der großen Halbachse der ellipsenförmigen Kurve, die die vektorielle Winkelgeschwindigkeit um diesen Pol beschreibt.

[DGLkombi2-16] Vernachlässigt man diesen Effekt, kommt man zu einer Näherung obiger Differentialgleichung für kleine Winkel zwischen den Ebenen:
${\dot {\vec {\omega }}}=-(A+B)\langle {\vec {\omega }},{\vec {n}}_{L}\rangle {\vec {n}}_{L}\times {\vec {\omega }},$
wobei ${\vec {n}}_{L}:=(A{\vec {n}}_{z}+B{\vec {n}}_{S})/(A+B)$ die Normale auf der Laplace-Ebene ist, die also gerade das gewichtete Mittel aus den Normalen auf Äquator- und Störbahnebene ist.

[Laplace-1] Pierre-Simon Laplace: Mécanique céleste. (Englische Übersetzung). Band 4. Little & Brown, Boston 1829, Kap. 17, S. 315 ff. (englisch, archive.org – französisch: Traité de Mécanique céleste. 1805. Übersetzt von Nathaniel Bowditch).

[2] R. R. Allan, G. E. Cook: The Long-Period Motion of the Plane of a Distant Circular Orbit, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 280, No. 1380 (Jul. 7, 1964), pp. 97–109

[Laplace2-3] S. Laplace, Kap. IV, S. 62ff.

[TUM-5] Satellitenbahnen Projekt TU-München (Memento des Originals vom 30. September 2007 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2

[daten-8] NASA Earth Fact Sheet

[jupiter-9] NASA Jupiter Fact Sheet (Memento des Originals vom 5. Oktober 2011 auf WebCite) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2

[JPL-10] Planetary Satellite Mean Orbital Parameters vom JPL

[schneider1-12] M. Schneider: Himmelsmechanik, Kap. 26, Bd. 2, BI Wiss. Verlag, Mannheim (1993), S. 542--550