Längenproblem
Der Ausdruck Längenproblem oder Längengradproblem bezeichnet das lange ungelöste Problem, die geographische Länge beispielsweise eines Schiffes auf dem offenen Meer bestimmen zu können.
Während die geographische Breite anhand des Sternhimmels relativ einfach mit für die Seefahrt hinreichender Genauigkeit messbar ist, ist eine vergleichbar genaue Bestimmung der Länge weitaus schwieriger. Das liegt daran, dass die Breitenkreise durch die Erdrotation eine physikalische Bedeutung haben, während die Längenkreise eine rein willkürliche Einteilung darstellen. Zur Bestimmung der Länge eines beliebigen Orts wird als Referenz die genaue Sonnenzeit an einem Ort mit bekannter Länge benötigt. Aus der Differenz zur Ortszeit des Schiffes ergibt sich die Längendifferenz. In der Ermittlung dieser genauen Referenzzeit lag das Problem, solange hinreichend genaue Uhren technisch nicht machbar waren.
Ohne Möglichkeit zur genauen Bestimmung der geographischen Länge war es riskant, ein weit entferntes Ziel auf kürzestem Weg anzusteuern, da Kursabweichungen nicht erkannt werden konnten. Als zuverlässige indirekte Navigationsmethode wurde das Breitensegeln genutzt, das jedoch die Wegstrecke und damit die Reisedauer erheblich verlängerte.[1] Deshalb hatte der König von Spanien bereits 1600 einen Preis für eine Lösung ausgesetzt, damals erfolglos.
Das Längenproblem wurde erst nach 1750 mit den sehr ganggenauen Schiffsuhren Harrisons zufriedenstellend gelöst.
Erst die Einführung satellitengestützter Positionsmessung in den 1960er Jahren bot eine von Zeitmessungen unabhängige Möglichkeit der exakten Längenfeststellung auf hoher See.
Ein gesamteuropäisches Problem
Die Gründung des königlichen Observatoriums in Greenwich durch Karl II. im Jahr 1675 war Englands erster Schritt auf der Suche nach einer genauen Längenmessung. Auch in Paris (Pariser Sternwarte) und St. Petersburg wurden Observatorien gegründet.
Nach der Schiffskatastrophe bei den Scilly-Inseln 1707, bei der ein Flottenverband unter Admiral Cloudesley Shovell bei der Fahrt von Gibraltar nach Portsmouth auf die Scilly-Inseln aufgelaufen war und dabei 4 der 21 Schiffe mit 1.450 Seeleuten verloren hatte, gewann das Problem der genauen Positionsbestimmung auf hoher See wieder an Dringlichkeit. Nach einer Petition von William Whiston und Humphry Ditton (untermauert durch Stellungnahmen von Isaac Newton und Edmond Halley) lobte 1714 das britische Parlament für eine praktisch brauchbare Lösung des Längenproblems ein hohes Preisgeld aus: bei einer Genauigkeit von höchstens einem halben Grad Abweichung 20.000 £ und bei einer Genauigkeit bis zu einem Grad Abweichung 10.000 £. Ein Längenunterschied von einem Grad entspricht am Äquator 60 Seemeilen (etwa 111 km) und nimmt zu den Polen hin ab. Auf der Breite des Ärmelkanals entspricht ein Längengrad noch rund 40 Seemeilen (etwa 74 km). Eine Uhr darf nicht mehr als 4 Minuten falsch anzeigen, um diese für die Seefahrt immer noch viel zu geringe Genauigkeit zu ermöglichen.
Das Preisgeld bedeutete damals ein stattliches Vermögen, vergleichbar mit einem heutigen zweistelligen Millionenbetrag. Ein seegängiges Schiff mittlerer Größe kostete damals etwa 1.500 bis 2.500 £, ein einfacher Arbeiter lebte von 10 £ im Jahr. Zur Verwaltung des Preisgeldes und zur Beurteilung eingereichter Vorschläge wurde die „Längenkommission“ gegründet, das Board of Longitude, der die damals bedeutendsten Astronomen und Mathematiker Englands angehörten, aber auch der Präsident der Royal Society, der Königlichen Gesellschaft zur Förderung der Wissenschaften.
Mögliche Lösungswege
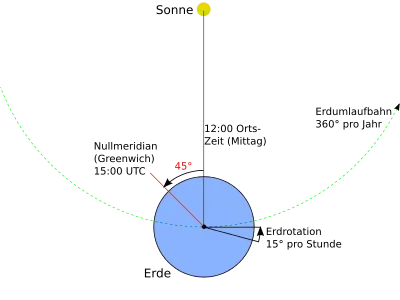
Alle möglichen Lösungen beruhen auf Zeitmessungen. Auf dem Schiff wird die lokale Sonnenzeit ermittelt, was anhand des Sonnenlaufes relativ einfach ist. Zusätzlich wird als Referenzzeit die aktuelle Sonnenzeit eines Ortes mit bekannter geographischer Länge benötigt. Aus der Zeitdifferenz kann man die Länge der eigenen Position errechnen, denn sie verhält sich zu 24 Stunden wie die Differenz der Längen zu 360°.
Beispiel: Auf dem Schiff ist Mittag, während es in Greenwich (0° Länge) 15:30 Uhr ist. Die Differenz der Zeit beträgt also 3,5 Stunden. Dann befindet man sich auf Länge, und zwar westliche Länge, da es in Greenwich später ist als an der eigenen Position.
Das Problem bestand darin, die genaue Referenzzeit zu kennen, also im obigen Beispiel zu wissen, wie spät es in Greenwich gerade ist. Brauchbare Methoden dafür bestehen entweder im Beobachten astronomischer Ereignisse, deren Zeitpunkte präzise vorausberechnet werden konnten und in einer Tabelle aufgelistet waren, oder im Mitführen einer Längenuhr, die während der ganzen Reise die Ortszeit des Referenzortes zeigt – ein Verfahren, das Gemma R. Frisius bereits 1530 vorgeschlagen hatte. Anfang des 18. Jahrhunderts war aber der Bau einer Uhr, die auf einem fahrenden Schiff mit seinen Bewegungen unter wechselnden klimatischen Bedingungen genügend genau geht, technisch noch nicht möglich, so dass zunächst auf die astronomischen Beobachtungen gesetzt wurde.
Jupitermonde
Die von Galilei (1564–1642) entdeckten Jupitermonde umkreisen den Jupiter so schnell, dass rund 1000-mal jährlich ein exakt vorausberechenbares Erscheinen oder Verschwinden eines Mondes eintritt. Diese Ereignisse sind für alle Beobachtungsorte auf der Erde praktisch gleichzeitig beobachtbar und daher als globale „Zeitmarken“ geeignet. Diese Lösung war jedoch auf ein ruhig stehendes Teleskop angewiesen und damit nur an Land zuverlässig nutzbar.
Dennoch bemühten sich Wissenschaftler aus verschiedenen Nationen zumindest auf dem Festland mittels Beobachtung der Jupitermonde um exakte Längengradbestimmungen. Darunter waren Giovanni Domenico Cassini, Erasmus Bartholin, Ole Rømer und Jean-Philippe Baratier.
Mond
Gut zu beobachten ist hingegen der Erdmond, dessen Bewegung allerdings erst durch aufwendige Berechnungen auf Basis genauer Beobachtungen vorhergesagt werden konnte. Weitaus früher konnten jedoch Mondfinsternisse vorausberechnet werden.
Mondfinsternisse
Viele dieser Erscheinungen sind von beinahe der halben Erdoberfläche aus beobachtbar, und durch Vergleich der Zeitpunkte des Ein- und Austritts des Erdschattens auf dem Mond lassen sich Differenzen der geographischen Längen der einzelnen Beobachter bestimmen. Dieses Verfahren wurde nachweislich von Plinius (ca. 23–79) und Ptolemäus (ca. 100–ca. 175) angewandt.
Die Finsternis am 24. Mai 997 wurde von Al-Biruni in Xiva und Abu l-Wafa in Bagdad zwecks Bestimmung der Längenunterschiede beobachtet.
Christoph Kolumbus hatte zwar Vorausberechnungen des Regiomontanus zur Verfügung, versuchte damit aber in der Karibik zweimal erfolglos, durch Beobachtung von Finsternissen seine geographische Länge zu bestimmen (1494, 1504).
Monddistanzen
Der Mond vollzieht innerhalb von gut 27 Tagen einen Vollkreis vor dem Sternenhintergrund und bewegt sich damit so zügig (etwa ein halbes Grad pro Stunde), dass eine genaue Messung seines Winkelabstandes zu einem hellen Fixstern in der Nähe seiner Bahn eine gute Zeitreferenz ergibt.
Diese Methode wurde erstmals von Johannes Werner in seinem Werk „In hoc opere haec continentur Nova translatio primi libri geographiae Cl' Ptolomaei…“ (Nürnberg 1514) erwähnt, erlangte aber erst Beachtung, als Peter Apian sie in seinem „Cosmographicus liber…“ (Landshut 1524) genauer erörterte. Viele Observatorien, unter anderem das in Greenwich, wurden eigens zu dem Zweck gegründet, den Mondlauf so genau zu vermessen, dass präzise Monddistanzen auf Monate im Voraus berechnet werden konnten.
Edmond Halley, der im Zusammenhang mit dem Längenproblem 1698 und 1700 zwei Reisen unternommen hatte, scheiterte an der Unzulänglichkeit seiner 1661 von Thomas Street errechneten Mondtafeln und unterstützte dann als einer der wenigen Wissenschaftler den Ansatz John Harrisons mit dessen Schiffsuhren, erlebte aber dessen Durchbruch nicht mehr.
Vorangebracht wurde die Monddistanzenmethode von dem deutschen Kartographen und Mathematiker Tobias Mayer (1723–1762), der 28-jährig, ohne ein reguläres Studium absolviert zu haben, in Göttingen einen Lehrstuhl für Mathematik erhielt. Während seiner Arbeit bei einem Kartenverlag in Nürnberg entwickelte er die ersten brauchbaren Mondtabellen, basierend auf mathematischen Berechnungen. Diese wurden von Sir Nevil Maskelyne (1732–1811) übersetzt und bearbeitet und boten noch lange Zeit eine billige Methode der Zeitfeststellung.
James Cook hatte auf seiner ersten Südseereise (1768–1771) Maskelynes Bearbeitung von Mayers Tabellen zur Verfügung. 1767 wurde erstmals der danach jährlich erscheinende Nautical almanac and astronomical ephemeris veröffentlicht, in dem Mondtabellen abgedruckt wurden, welche die Winkelabstände des Mondes zu sieben Fixsternen zu jeder vollen Stunde auflisteten. Cook hatte auf dieser Reise auch einen Astronomen an Bord.
Maskelyne hat Erläuterungen zu seiner aufwendigen Berechnungsmethode veröffentlicht. In den folgenden Jahrzehnten entstanden zahlreiche einfachere Näherungsmethoden. Besonders die von Nathaniel Bowditch (1773–1838) vorgeschlagene Methode fand über sein berühmtes (noch heute erscheinendes) Navigationshandbuch American Practical Navigator weite Verbreitung. Der „Bowditch“ führte entsprechende Hilfstabellen immerhin bis 1914, obwohl im Nautical Almanac schon Jahre zuvor keine Monddistanzen mehr enthalten waren.
Der Vorteil der Monddistanzen-Methode lag in ihrer kostengünstigen Umsetzung: Sextanten waren auf den Schiffen bereits vorhanden, da sie ohnehin zur Breitenmessung benötigt wurden. Somit mussten nur die vorberechneten Distanzentafeln vervielfältigt und verteilt werden. Nachteilig war, dass die Bestimmung einer Monddistanz nur in einer hinreichend klaren Nacht bei sichtbarem Mond möglich war; um Neumond herum war die Methode praktisch nicht anwendbar.
Schiffsuhr
Einen ganz anderen und letztlich erfolgreichen Weg beschritt der gelernte Tischler John Harrison: Eine besonders präzise laufende Uhr an Bord würde es ermöglichen, eine beliebige Referenzzeit auf die Seereise „mitzunehmen“ und jederzeit ablesen zu können.
Diese Methode machte alle aufwendigen Beobachtungen, Vorausberechnungen und Tabellen überflüssig. Das Problem lag in der Genauigkeit der Uhr: Bis um 1700 galten Uhren mit nur einer Minute Abweichung pro Tag schon als hochpräzise und technisch kaum realisierbar – das galt für ruhende Uhren auf festem Boden. Jede Bewegung lässt eine mechanische Uhr weniger genau gehen, und schon eine Zeitabweichung von zehn Minuten entspricht auf dem Äquator 2,5 Längengraden oder rund 280 km. Auf einem Schiff ist die Uhr ständig in Bewegung und dazu noch wechselnden Klimaten und Temperaturen ausgesetzt, was die Genauigkeit beeinträchtigt. Die Konstruktion einer Uhr, die unter den realen Bedingungen einer monatelangen Schiffsreise nur um wenige Minuten abweicht, schien unmöglich.
Um dieses Problem zu lösen, ersann Harrison verschiedene Uhrenkonzepte mit gegenläufig-gekoppelten Mechaniken, deren Gangfehler bei schwankender Bewegung einander ausglichen, und stellte der Längengradkommission 1728 ein erstes Konzept sowie 1735 eine erste funktionsfähige Uhr vor. Doch das Gremium verzögerte die Würdigung und Anerkennung seiner Arbeit um Jahrzehnte, teils aus politisch-strategischen Gründen, aber auch deshalb, weil die führenden Wissenschaftler den Vorschlag eines einfachen Handwerkers nicht ernst nehmen wollten. Newton bezweifelte grundsätzlich die technische Machbarkeit einer hinreichend genauen Uhr, obwohl Harrison bereits 1725 mechanische Standuhren mit sehr geringen Gangfehlern gefertigt hatte. Der Astronom Sir Nevil Maskelyne, der selbst die Monddistanzenmethode propagierte, änderte die Auslegung der Ausschreibung zu Harrisons Ungunsten, vor allem, nachdem er 1765 königlicher Astronom geworden war. Harrison waren auch sein eigener Erfindergeist und sein Perfektionismus hinderlich: Jede seiner Uhren unterschied sich erheblich von den früheren, so dass er ständig neue Konzepte vorstellte, was seiner Glaubwürdigkeit schadete. Man verlangte beispielsweise von ihm, seine Pläne anderen Uhrmachern auszuhändigen und die Modelle von diesen fertigen zu lassen, um Mogeleien auszuschließen.
Eine Taschenuhr mit einem neuartigen Antrieb, die Harrison 1753 für sich selbst anfertigen ließ, bewog ihn schließlich zu einem vollkommen neuen vierten Konzept, an dem er bis 1759 arbeitete. Dieses brachte nach mehr als drei Jahrzehnten den Durchbruch: Beim Test auf einer mehrmonatigen Seereise nach Jamaika summierte sich der Gangfehler der später als „H4“ bezeichneten Uhr auf weniger als zwei Minuten.
Andere Vorschläge
Aufgrund des hohen Preisgeldes wurden auch ungeeignete und absurde Ideen für die Lösung des Längenproblems hervorgebracht und teilweise öffentlich diskutiert. Ein sehr abstruser Vorschlag war schon 1687 in dem Flugblatt Curious Enquiries veröffentlicht worden:
- Zunächst werde ein Hund vor Antritt der Reise mit einem Messer verwundet. Der Hund gehe mit auf die Reise, das Messer bleibe im Heimathafen. Dann werde im Heimathafen täglich genau zur Mittagszeit Waffensalbe auf dieses Messer aufgebracht, was aufgrund einer übernatürlichen Verbindung zwischen Waffe und Wunde den Hund an Bord des Schiffes vor Schmerz aufheulen lasse und der Schiffsbesatzung damit den Mittagszeitpunkt im Heimathafen kundtue. (Dieses Verfahren griff Umberto Eco in seinem Roman Die Insel des vorigen Tages auf.)
Die Mathematiker William Whiston und Humphry Ditton schlugen vor, in gleichmäßigen Abständen Schiffe im Meer zu verankern, die mehrmals täglich durch Böllerschüsse bei der Positionsbestimmung helfen sollten: Aus dem Zeitunterschied zwischen Blitz und Knall wäre der Abstand zum Böllerschiff errechenbar. Whiston, ein Schüler Newtons, war dabei von 600 m maximaler Wassertiefe der Ozeane ausgegangen. Dieses Verfahren erwies sich auf See als nicht anwendbar, jedoch hat es Anwendungen an Land gegeben.
Ernsthaft in Erwägung gezogen wurde die Auswertung von Ungleichmäßigkeiten des Erdmagnetfelds, mit denen sich Edmond Halley, William Whiston, Christoph Semler beschäftigten. Diese Vorschläge erwiesen sich aber schon bald als unpraktikabel.
Die Lösung
Erst als James Cook 1775 nach der Heimkehr von seiner zweiten Weltreise die Brauchbarkeit des time keepers begeistert lobte, den Larcum Kendall in Harrisons Auftrag als exakte Kopie der Uhr von 1759 gebaut hatte, galt auch den meisten Astronomen das Längenproblem als gelöst. Im Logbuch nennt der zunächst skeptische Cook Kendalls Werk seinen „nie versagenden Führer“: Eine Uhr „nahm die Uhrzeit des Ausgangshafens mit auf die Reise“. Drei weitere Uhren, die Cook ebenfalls zu testen hatte, waren den Belastungen der Reise nicht gewachsen.
John Harrison erhielt nach langem Ringen kurz vor seinem Tod den letzten Anteil des ihm zustehenden Preisgeldes. Postum wurden auch Tobias Mayer £3000 zugesprochen und seiner Witwe ausgehändigt.
1780 prägte John Arnold für seine Weiterentwicklung von Harrisons Uhr den Begriff des Chronometers. Bis jedes Schiff mit einem der zunächst noch sehr kostspieligen Chronometer ausgestattet war, wurden weiterhin Maskelynes Mondtabellen verwendet. Zuerst rüstete die Britische Ostindien-Kompanie ihre Schiffe mit Chronometern aus, die Umstellung der Royal Navy dauerte bis 1840. Kapitäne kleinerer Handelsschiffe arbeiteten noch einige Jahrzehnte mit Monddistanzen, bis preisgünstigere Chronometer auf den Markt kamen.
Nach der Lösung des Problems wurde das Board of Longitude 1828 aufgelöst und durch das Resident Committee for Scientific Advice for the Admiralty (‚Komitee zur wissenschaftlichen Beratung der Admiralität‘) ersetzt.
Literatur
- Dava Sobel, William J. H. Andrewes: Längengrad – die illustrierte Ausgabe. Die wahre Geschichte eines einsamen Genies, welches das größte wissenschaftliche Problem seiner Zeit löste. Berlin-Verlag, Berlin 2010, ISBN 3-8270-0970-7 (englisch: Longitude. Übersetzt von Matthias Fienbork und Dirk Muelder).
- Johann Matthias Hassencamp: Kurze Geschichte der Bemühungen die Meereslänge zu erfinden. Rinteln 1769.
- Johann Samuel Traugott Gehler’s physicalisches Wörterbuch. Vol. 6 Abth. 1, 1834
- Peter Boy Andresen: Die Geschichte der Monddistanzen. Marbach 1986 (Nachdruck der Ausgabe Hamburg 1924).
- William J. H. Andrewes (ed.): The Quest for Longitude. Cambridge, Mass. 1996.
- Erwin Roth: Tobias Mayer, 1723–1762. Vermesser des Meeres, der Erde und des Himmels. Esslingen 1985.
- Umberto Eco: Die Insel des vorigen Tages.
- Joan Dash (Übersetzung aus dem Amerikanischen von Tamara Willmann): Die Jagd nach dem Längengrad. Jugendbuch im Verlag C. Bertelsmann, ISBN 3-570-12717-6.
- Felix Lühning: Längengrad. Kritische Betrachtung eines Bestsellers. In: Beiträge zur Astronomiegeschichte, Band 10. Frankfurt a. M. 2010, S. 104–186 (zu Dava Sobel: Längengrad).
- Wolfgang Köberer: Instrument unde Declinatie der Sünnen, Das älteste niederdeutsche Navigationshandbuch von Jacob Alday aus dem Jahr 1578. Faksimile, Transkriptions- und Kommentarband, Edition Stiedenrod, Wiefelstede 2009.
Spielfilm
Das Längenproblem und seine Lösung durch John Harrison ist auch Gegenstand eines Spielfilms unter dem Titel Der Längengrad – Longitude mit Jonathan Coy, Christopher Hodsol und Jeremy Irons in den Hauptrollen. Der Film wurde nach der Vorlage des Buchs Längengrad von Dava Sobel gedreht.
Weblinks
- Frank Slomka: Das Längengradproblem. YouTube-Video, 27:21 min.
Einzelnachweise
- Mike Dash: De Ondergang Van De Batavia. Singel Pockets, Amsterdam 2005, ISBN 978-90-413-3124-3.