Kongruente Zahl
In der Zahlentheorie sind kongruente Zahlen ganze Zahlen, welche sich als Flächeninhalt eines rechtwinkligen Dreiecks mit rationalen Seitenlängen darstellen lassen. Historisch namensgebend sind "sich treffende" (lat. congruere) arithmetische Folgen von Quadratzahlen, womit auf von Leonardo Fibonacci eingeführte congruum, pl. congrua verwiesen wird, welche mit einem geeigneten rationalen Quadrat multipliziert die kongruente Zahlen bilden. Édouard Lucas bewies 1877 für kongruente Zahlen n den Zusammenhang mit rationalen Lösungen der Gleichung: . Kurt Heegner war der erste, der das Problem kongruenter Zahlen mit elliptischen Kurven verband, und 1952 bewies er, dass eine Primzahl eine kongruente Zahl ist, wenn oder .
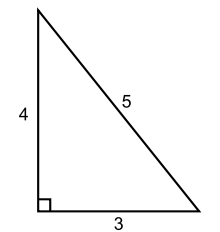
Die Folge der kongruenten Zahlen (Folge A003273 in OEIS) beginnt mit
- 5, 6, 7, 13, 14, 15, 20, 21, 22, 23, 24, 28, 29, 30, 31, 34, 37, 38, 39, 41, 45, 46, 47, …
| Tabelle der kongruenten Zahlen: n ≤ 120[1] | ||||||||
|---|---|---|---|---|---|---|---|---|
| —: Nicht-Kongruente Zahl K: Quadratfreie Kongruente Zahl Q: Kongruente Zahl mit quadratischem Faktor | ||||||||
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| — | — | — | — | K | K | K | — | |
| n | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| — | — | — | — | K | K | K | — | |
| n | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| — | — | — | Q | K | K | K | Q | |
| n | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| — | — | — | Q | K | K | K | — | |
| n | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| — | K | — | — | K | K | K | — | |
| n | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| K | — | — | — | Q | K | K | — | |
| n | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 |
| — | — | — | Q | K | Q | K | Q | |
| n | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 |
| — | — | — | Q | K | K | Q | — | |
| n | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 |
| K | — | — | — | K | K | K | — | |
| n | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| — | — | — | — | K | K | K | Q | |
| n | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 |
| — | — | — | Q | K | K | K | Q | |
| n | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 |
| — | — | — | Q | K | K | K | Q | |
| n | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 |
| — | — | — | — | K | K | K | — | |
| n | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 |
| — | — | — | — | K | K | K | Q | |
| n | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| — | — | — | Q | Q | K | K | Q | |
Beispiel: Die ganze Zahl 6 ist eine kongruente Zahl, denn das rechtwinklige Dreieck mit den Katheten und besitzt den Flächeninhalt und nach dem Satz des Pythagoras die Hypotenuse . Also ist die ganze Zahl 6 als Flächeninhalt eines rechtwinkligen Dreiecks mit rationalen Seitenlängen eine kongruente Zahl.
Für jede positive ganze Zahl ist eine ganze Zahl genau dann eine Kongruenzzahl, wenn eine Kongruenzzahl ist. Deshalb kann man sich bei der Lösung des Kongruenzzahl-Problems auf quadratfreie Zahlen beschränken.
Allgemeiner werden auch alle rationalen Zahlen, die als Fläche eines rechtwinkligen Dreiecks mit rationalen Seitenlängen auftreten, als kongruente Zahlen bezeichnet.[2]
Kongruente Zahlen im Bereich 1 bis 20
Die folgenden ganzen Zahlen im Bereich 1 bis 20 sind kongruent,[3] da sie sich als Flächeninhalt eines rechtwinkligen Dreiecks mit rationalen Katheten und und rationaler Hypotenuse darstellen lassen:
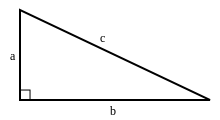
| Flächeninhalt | Kathete | Kathete | Hypotenuse |
|---|---|---|---|
Satz von Fermat
Der französische Mathematiker Pierre de Fermat bewies, dass die Fläche eines rechtwinkligen Dreiecks mit ganzzahligen Seitenlängen keine Quadratzahl sein kann. Dies ist äquivalent dazu, dass weder 1 noch jede andere Quadratzahl eine kongruente Zahl ist. Sein Resultat teilte er 1659 in einem Brief an Pierre de Carcavi mit,[4] den Beweis notierte er in einer Anmerkung, die 1670 postum veröffentlicht wurde.[5][6] Fermat geht von der seit der Antike bekannten Darstellung eines primitiven pythagoreischen Tripels als (x2−y2, 2xy,x2+y2) aus und verwendet die von ihm eingeführte Methode des unendlichen Abstiegs, eine Variante der vollständigen Induktion. Sein Beweis zeigt auch, dass die Gleichung a4+b4=c4 keine Lösung mit positiven ganzen Zahlen a, b, c hat (ein Spezialfall der Fermatschen Vermutung).[7]
Satz von Tunnell
Der Satz von Tunnell, benannt nach Jerrold B. Tunnell, gibt notwendige Bedingungen dafür, dass eine Zahl kongruent ist.
Für eine quadratfreie ganze Zahl definiere
Wenn eine ungerade Kongruenzzahl ist, dann muss sein, wenn eine gerade Kongruenzzahl ist, dann muss sein.
Falls die Vermutung von Birch und Swinnerton-Dyer für elliptische Kurven der Form gilt, dann sind diese Bedingungen auch hinreichend. Dann wäre die natürliche Zahl n genau dann kongruent, wenn die abelsche Gruppe der rationalen Punkte der elliptischen Kurve einen Rang mindestens 1 hat.
Pan Yan bewies 2014 dies bedingt (schwache Form der Vermutung von Birch und Swinnerton-Dyer) für alle positiven quadratfreien ganzen Zahlen .[8] In Weiterführung dieser Ideen zeigte Alexander Smith 2016, dass mindestens 55,9 Prozent der positiven quadratfreien ganzen Zahlen kongruente Zahlen sind.[9]
Literatur
- Leonard Eugene Dickson: Congruent numbers in History of the theory of numbers. Volume II: Diophantine equations, Carnegie Institution, Washington 1920, S. 459–472 (englisch)
- J. B. Tunnell: A classical Diophantine problem and modular forms of weight 3/2, Inventiones mathematicae 72 (2), 1983, S. 323–334 (englisch)
Einzelnachweise
- Folge A003273 in OEIS
- Neal Koblitz: Introduction to elliptic curves and modular forms, Springer-Verlag, 1984, 2. Auflage 1993, ISBN 3-540-97966-2, S. 3 (englisch)
- Kongruente Zahlen: Tausend Jahre altes Geometrierätsel, Spiegel Online, 31. Januar 2013
- Paul Tannery, Charles Henry (Hrsg.): Œuvres de Fermat. Tome deuxième, Gauthier-Villars, Paris 1894, S. 431–436 (französisch)
- Samuel de Fermat (Hrsg.): Diophanti Alexandrini Arithmeticorum libri sex, et de numeris multangulis liber unus, Bernard Bosc, Toulouse 1670, S. 338f.; auch in Paul Tannery, Charles Henry (Hrsg.): Œuvres de Fermat. Tome premier, Gauthier-Villars, Paris 1891, S. 340f. (lateinisch)
- Catherine Goldstein: Un théorème de Fermat et ses lecteurs, Presse Universitaire de Vincennes, St. Denis 1995, ISBN 2-910381-10-2 (französisch; Inhaltsverzeichnis, PDF-Datei, 29,4 kB; Rezension, Zentralblatt-Rezension)
- H. G. Zeuthen: Geschichte der Mathematik im XVI. und XVII. Jahrhundert, B. G. Teubner, Leipzig 1903, S. 163f.
- Pan Yan, Congruent Numbers and Elliptic Curves, math.okstate.edu
- Smith, The congruent numbers have positive natural density, Arxiv 2016
Weblinks
- Holger Dambeck: Mathematik: Lösung für Rätsel aus 1001 Nacht rückt näher. Spiegel Online, 31. Januar 2013, abgerufen am 1. Februar 2013.