Bitwertigkeit

Die Bitwertigkeit legt den Stellenwert eines einzelnen Bits fest, den es durch seine Position innerhalb einer Binärzahl (auch Dualzahl genannt) haben soll. Wichtig ist diese Festlegung auch bei der seriellen Datenübertragung sowie für parallele Busse in der Datenverarbeitung.

Werden acht Bits zu Bytes gruppiert und diese wiederum zu größeren Zahlenformaten, so ist zusätzlich die Byte-Reihenfolge festzulegen.

Die Bitnummerierung ist unabhängig von der Byte-Reihenfolge (Byte-Endianness) und von der „Bit-Endianness“.

LSB-0-Bitnummerierung

8-Bit-Zahl mit Bit 0 als dem LSB („LSB 0“)
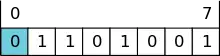Dieselbe 8-Bit-Zahl, gespiegelt, mit „LSB 0“

Sind die Bits innerhalb einer Binärzahl gemäß LSB 0 nummeriert, dann hat das Bit mit dem niedrigsten Stellenwert (Englisch least significant bit) die Nummer 0 (= ist das Bit mit dem Index 0).

Ist bei einer Binärzahl mit den Stellen $0,1,\ldots ,N-1$ die Bitposition 0 die niedrigstwertige, dann ist deren Wert mit $1$ zu multiplizieren. Der Gesamtwert der Binärzahl ist:

\sum _{i=0}^{N-1}a_{i}\cdot 2^{i}

MSB-0-Bitnummerierung

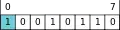Dieselbe 8-Bit-Zahl mit Bit 0 als dem MSB („MSB 0“)
Dieselbe 8-Bit-Zahl, gespiegelt, mit „MSB 0“

Sind die Bits innerhalb einer Binärzahl gemäß MSB 0 nummeriert, dann hat das Bit mit dem höchsten Stellenwert (Englisch most significant bit) die Nummer 0 (= ist das Bit mit dem Index 0).

Ist bei einer Binärzahl mit den Positionen $0,1,\ldots ,N-1$ die Bitposition 0 die höchstwertige, dann ist deren Wert mit $2^{N-1}$ zu multiplizieren. Der Gesamtwert der Binärzahl ist:

\sum _{i=0}^{N-1}a_{i}\cdot 2^{N-1-i}

Bit-Reihenfolge

Werden die Stellen gemäß ihrer absteigenden Wertigkeit horizontal von links nach rechts aufgetragen (das sind jeweils die linken Abbildungen in den beiden vorherigen Abschnitten; möglich ist auch der umgekehrte / gespiegelte Fall: die Stellen gemäß ihrer absteigenden Wertigkeit horizontal von rechts nach links aufzutragen, das sind die beiden rechten Abbildungen), so hängt es von der Bit-Reihenfolge ab, auf welcher Seite mit der Bit-Nummerierung begonnen wird:

Beginnt die Zählung mit 0 für das niedrigstwertige Bit (LSB) auf der rechten Seite und läuft nach links, so spricht man von „LSB₀“.
Beginnt die Zählung mit 0 für das höchstwertige Bit (MSB) auf der linken Seite und läuft nach rechts, so spricht man von „MSB₀“.

Beispiel: Die 8-Bit-Zahl 220_dez mit *MSB₀* und *LSB₀*
		MSB							LSB
Bitnummer bei	LSB 0	7	6	5	4	3	2	1	0
Bitnummer bei	MSB 0	0	1	2	3	4	5	6	7
Inhalt des Bit		1	1	0	1	1	1	0	0
Stellen-Wert (dezimal)		128	64	32	16	8	4	2	1

Zahlenformat und Vorzeichenbit

Das höchstwertige Bit (MSB) zeigt im Einerkomplement, Zweierkomplement und anderen Zahlenformaten mit Vorzeichenbit auch an, ob die entsprechende Dezimalzahl positiv oder negativ ist. Beim Zweierkomplement zählt die Null dabei zu den nicht-negativen Zahlen, sodass man mehr negative als positive Zahlen darstellen kann. Bei anderen Zahlenformaten wie dem Einerkomplement oder Gleitkommazahlen nach IEEE-754-Standard gibt es zwei Darstellungen der Null (+0 und −0).

Adressierung von Bits

Dieselben Annahmen wie im Artikel „Byte-Reihenfolge“ seien vorausgesetzt.

Für die meisten in der Praxis verwendeten Rechner besteht die kleinste adressierbare Einheit aus mehr als einem Bit, z. B. aus einem Byte, das 8 Bits enthält. Mithin lässt sich ein einzelnes Bit nicht unmittelbar adressieren.

Fügt man einer Byte-Adresse jedoch ein Bit-Offset BitOffset ∈ 0,1, …,7 bei, so wird ein einzelnes Bit eindeutig spezifizierbar. Diese Art der Spezifikation wird Bit-Adressierung genannt. Sie lässt sich über den Umweg von Register verschiebungen verwirklichen.

Die Begriffe links/rechts haben bei solchen Shift-Befehlen nichts mit links/rechts wie weiter oben beschrieben zu tun, sondern orientieren sich ausschließlich an der üblichen Sicht:

der Links-Shift multipliziert eine Binärzahl mit einer Zweierpotenz, verschiebt die Bits also in Richtung „Big-End“ (= Richtung most significant bit)
der Rechts-Shift umgekehrt.

In der Form ByteAdresse * 8 + BitOffset hat die Bit-Adressierung folgende Eigenschaften:

Adress- Inkrement	Links -Shift	Rechts -Shift
Big-Endian	–1	+1
Little-Endian	+1	–1

Abgesehen von den Effekten an den beiden Rändern des Registers, bedeutet eine Shift-Operation um 1 Bit eine Veränderung der Bit-Adresse um 1 (genauer: einen Transport der Bitkette an eine um 1 veränderte Bitadresse), und zwar entspricht (vgl. Tabelle):
- ein Links-Shift bei Big-Endian einer Verringerung um 1,
- ein Rechts-Shift bei Big-Endian einer Erhöhung um 1,
- ein Links-Shift bei Little-Endian einer Erhöhung um 1,
- ein Rechts-Shift bei Little-Endian einer Verringerung um 1.
Unmittelbar erkennbar wird dies bei Shifts um Vielfache von 8 Bits: Eine Shift-Operation um 8 Bit ist dasselbe wie 8 Shift-Operationen um 1 Bit in immer die gleiche Richtung. Von den Randeffekten abgesehen bedeutet ein Shift um 8 Bit eine Veränderung der Byte-Adresse um 1 (Verringerung / Erhöhung wie oben bei einzelnen Bits).
Damit aber eine Shift-Operation um 8 Bit nicht nur aus Randeffekten besteht, muss das Register breiter als 8 Bit sein.

Ergebnis

Die Unterscheidbarkeit der Bits lässt sich abbilden auf eine eindeutige Adressierung (Nummerierung) derselben, bspw. in der exemplarischen Form ByteAdresse * 8 + BitOffset . Der Zugriff auf ein einzelnes Bit gelingt (nach entsprechender Isolierung durch bitweise Operationen) unter Zuhilfenahme von Shift-Operationen. Rechts- wie Links-Shift führen (auf ein und demselben Computer) beide zum exakt gleichen Ergebnis. Dabei wird die Endianness (Big oder Little) der Bytes im Wort auf eine der Bits im Byte übertragen.
Die Shift-Operationen stellen unter dieser Adressierung Transporte von Bits dar um die im Shift angegebene Anzahl von Bit-Positionen.

Platziert man in der horizontalen Darstellung die niedrigen Adressen links und die hohen rechts, so lassen sich für 32 Bit (d. h. 4 Byte) lange Bit-Arrays oder vorzeichenlose Ganzzahlen die Konventionen der Bit-Nummerierung folgendermaßen gegenüberstellen:

Aufsteigende Offsets	Byte-Offset	0	1	2	3
Aufsteigende Offsets	Bit-Offset	0, 1, …, 7	0, 1, …, 7	0, 1, …, 7	0, 1, …, 7
Bitnummer bei Big-Endian und	MSB 0	0, 1, …, 7	08, …, 15	16, …, 23	24, …, 31
Bitnummer bei Big-Endian und	LSB 0	31, …, 24	23, …, 16	15, …, 08	7, …, 1, 0
Bitnummer bei Little-Endian und	LSB 0	0, 1, …, 7	08, …, 15	16, …, 23	24, …, 31
Bitnummer bei Little-Endian und	MSB 0	31, …, 24	23, …, 16	15, …, 08	7, …, 1, 0

Die Nummerierung der Bits bei Big-Endian mit MSB 0 und Little-Endian mit LSB 0 (beide farblich unterlegt) entspricht somit der Bit-Adresse.
Dagegen nummerieren die Konventionen LSB 0 bei Big-Endian und MSB 0 bei Little-Endian die Bits im Register gegenläufig zu ihrer Adresse, was mit einer (mit den Adressen aufsteigenden) Indizierung in einem Array antikorreliert.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.