Impulsfahrplan
Der Impulsfahrplan (englisch Lattice diagram, auch Wellenfahrplan) ist ein graphisches Verfahren, um den zeitlichen Verlauf eines Spannungssprungs längs einer elektrischen Leitung zu verfolgen. Ziel ist, die resultierende Kurvenform infolge der Reflexionen an den Kabelenden zu verstehen und zu berechnen.
Hintergrund
Schlägt beispielsweise ein Blitz in eine Freileitung ein, läuft ein Hochspannungspuls als Wanderwelle mit hoher Geschwindigkeit bis zu beiden Leitungsenden und wird dort wegen der normalerweise vorhandenen Fehlanpassung reflektiert.[1] Für diesen reflektierten Anteil gilt das Gleiche: Auch er läuft bis zum jeweils anderen Leitungsende und kann dort erneut reflektiert werden. Abhängig vom Reflexionsfaktor können sich Phase und Amplitude ändern und die Spannungssprünge werden immer kleiner. Bei praktisch aufgebauten Freileitungen kommt es durch die zur Vermeidung von Überspannung an den Leitungsenden angebrachten Überspannungsableiter zur teilweisen Absorption.
Bei einem Datenbus, der die Bausteine eines Computers verbindet, muss durch geeignete Abschlusswiderstände sichergestellt werden, dass keine störenden Pulsreflexionen auftreten können. Sollen genau zwei Bausteine angeschlossen werden, lassen sich unerwünschte Reflexionen einfach vermeiden. Sobald aber mehrere „Verbraucher“ an unterschiedlichen Stellen der Leitung angeschlossen werden müssen, kann es an jeder Verzweigung zu Signalreflexionen kommen, für deren Behandlung Impulsfahrpläne entwickelt wurden.
Graphische Darstellung
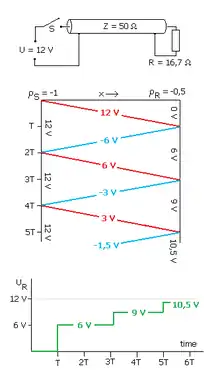
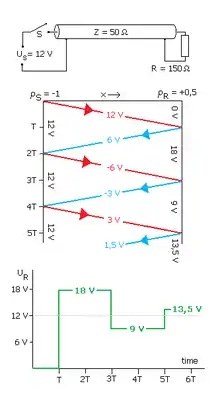
Signalreflexionen an falsch bemessenen Lastwiderständen lassen sich besonders einfach beschreiben, wenn sich die Spannung am Kabelanfang sehr schnell ändert und anschließend konstant bleibt. Dieser Spannungssprung durcheilt das Kabel mit fast Lichtgeschwindigkeit und kann am Kabelende – abhängig vom Reflexionsfaktor – reflektiert werden. Anschließend ist Lastspannung für den Zeitraum 2·T konstant und errechnet sich wie bei jeder Superposition zu:
Das führt zu einem stufenförmigen Verlauf, der jeweils als unterstes Bild gezeigt ist und bei ausreichend langen Kabeln mit einem Oszilloskop überprüft werden kann. Die mittleren Bilder zeigen wie bei einem Bildfahrplan den Ort des Spannungssprunges (horizontale Achse) als Funktion der Zeit (vertikale Achse).
Für die nebenstehenden Bilder gelten folgende Annahmen:
- Die Spannung einer Stromversorgung mit dem Innenwiderstand RQuelle = 0 Ω springt zum Zeitpunkt t = 0 von Null auf 12 V. Für ankommende Spannungssprünge wirkt dieser Quellwiderstand wie ein Kurzschluss, der das Vorzeichen der Amplitude vertauscht.
- Die Leitung ist verlustfrei und besitzt den Wellenwiderstand Z = 50 Ω.
- Der Spannungssprung benötigt den Zeitraum T bis zum Leitungsende, wo ein Lastwiderstand R angeschlossen ist.
Ergebnisse für R < Z
Der Spannungssprung wird am Kabelende mit umgekehrtem Vorzeichen reflektiert und läuft abgeschwächt (Reflexionsfaktor ρ < 0) zurück zur Quelle. Erreicht er diese, wird er wegen RQuelle = 0 Ω mit vertauschtem Vorzeichen und gleicher Amplitude reflektiert. Die Spannung kann sich hier wegen RQuelle = 0 Ω nicht ändern.
Auffallend ist, dass die Lastspannung UR nur langsam den Endwert Us erreicht, obwohl keine große Kapazität aufgeladen werden muss (der Kapazitätsbelag des Kabels reicht bei weitem nicht aus zur Erklärung). Je geringer der Wert des Lastwiderstandes, desto länger dauert dieser Zeitraum, bei RLast = 0 Ω ist er selbstverständlich unendlich.
Ergebnisse für R > Z
Der Spannungssprung wird am Kabelende mit gleichem Vorzeichen reflektiert und läuft abgeschwächt (0 < ρ < 1) zurück zur Quelle.
Auffallend ist, dass die Lastspannung UR den Endwert Us in periodischen Abständen übertrifft, obwohl keine große Induktivität vorhanden ist. Bei unbelastetem Kabel (Leerlauf) kann UR den doppelten Wert von Us erreichen. Damit angeschlossene Schaltungen nicht zerstört werden, schützt man sie oft mit Varistoren. Der Spannungsverlauf am Lastwiderstand erinnert an eine gedämpfte Schwingung um den Sollwert Us. Je höher der Wert des Lastwiderstandes, desto länger dauert dieser Zeitraum, bei RLast = ∞ ist er unendlich.
Sonderfälle
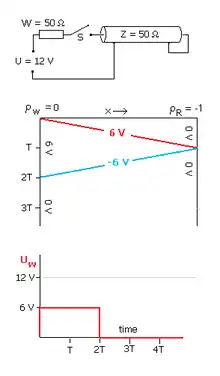
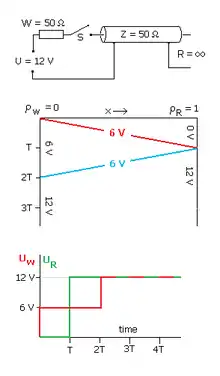
Schickt man einen Spannungssprung in ein Kabel, dessen Ende offen oder kurzgeschlossen ist, vereinfachen sich die messbaren Spannungsverläufe. Die mittleren Bilder zeigen den Ort des Spannungssprunges (horizontale Achse) als Funktion der Zeit (vertikale Achse), die unteren Bilder zeigen Oszillogramme. Es gelten folgende Annahmen:
- Die Spannung einer Stromversorgung mit dem Innenwiderstand W = Z = 50 Ω springt zum Zeitpunkt t = 0 von Null auf 12 V. Mit dieser Wahl werden ankommende Spannungssprünge reflexionsfrei absorbiert.
- Die Leitung ist verlustfrei und besitzt den Wellenwiderstand Z = 50 Ω.
- Der Spannungssprung benötigt den Zeitraum T bis zum Leitungsende.
Kurzgeschlossenes Ende
Die Spannung am Kabelanfang hat zunächst wegen des Spannungsteilers aus W und Z den halben Wert der Quellenspannung. Sobald der gegenphasig reflektierte Sprung nach der Laufzeit 2T wieder am Kabelanfang ankommt, sinkt die Spannung auf null und verharrt dort. Da diese Zeitspanne sehr kurz gewählt werden kann, bezeichnet man das Verfahren auch als „elektronisches Differenzieren“. Mit dieser Schaltung lässt sich ein Messsignal, das schnell ansteigt und sehr langsam wieder abfällt, in einen kurzen Nadelimpuls verwandeln[2].
Offenes Ende
Die Spannung am Kabelanfang hat zunächst wegen des Spannungsteilers aus W und Z den halben Wert der Quellenspannung. Sobald der gleichphasig reflektierte Sprung nach der Laufzeit 2T wieder am Kabelanfang ankommt, verdoppelt sich die Spannung und bleibt auf diesem Niveau. Dann ist das Kabelstück „aufgeladen“.
Von technischer Bedeutung ist die zeitliche Umkehr als Impulsgenerator: Wird das mit der Spannung U „geladene“ Kabelstück schlagartig mit einem Lastwiderstand W = Z verbunden, liegt für den (kurzen) Zeitraum 2T die Spannung U/2 an. Der präzis rechteckige Spannungsverlauf kann mit Induktivitäten nur sehr schwer erreicht werden. Vorteilhaft ist der sehr hohe Wirkungsgrad, weil im Wellenwiderstand der Leitung keine Wärmeenergie umgesetzt wird.
Anwendungen
Befindet sich am Kabelende eine elektronische Schaltung, ist der Lastwiderstand meist nichtlinear. Beispielsweise sind bei CMOS-Schaltungen die Eingänge sehr empfindlich gegenüber statischen Aufladungen, weshalb meist Dioden gegen die beiden Betriebsspannungen integriert werden, um Überspannungen abzuleiten. Dann sind kompliziertere Verfahren erforderlich, um Kabelreflexionen zu berechnen.
Weblinks
- transmission_line_basics (MS PowerPoint; 806 kB)
- High Voltage Transient Analysis (PDF; 132 kB) - Alternativ (https://www.mrt.ac.lk/web/sites/default/files/elect/files/HV_Chap4.pdf)
Referenzen
- High Voltage Transient Analysis (Memento des Originals vom 29. Juni 2012 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis. (PDF; 132 kB)
- Dieter Suter: Elektronik. (PDF; 3,8 MB) Archiviert vom Original am 4. Juli 2017; abgerufen am 1. Mai 2017.