Bergeron-Verfahren

Das Bergeron-Verfahren ist eine grafische Methode der Leitungstheorie, um auf verlustlosen Leitungen das Verhalten eines einzelnen Schaltvorgangs bei Reflexionen an nichtlinearen, speicherfreien (resistiven) Generator- und Lastzweipolen qualitativ und soweit es die Genauigkeit zulässt quantitativ zu ermitteln. Als Ergebnis des grafischen Verfahrens entsteht das sogenannte Bergeron-Diagramm.

In der Impulstechnik und der Digitalelektronik müssen kurze Impulse mit steilen Signalflanken über Verbindungsleitungen möglichst ohne Formverfälschung übertragen werden. In solchen Fällen kann das Bergeron-Verfahren zur Analyse der Reflexionen an nichtlinearen Schaltkreisaus- und -eingängen dienen. Ein typischer Anwendungsfall ist die Untersuchung des negativen Überschwingens bei TTL-Schaltkreisen.

Das Verfahren wurde erstmals in den 1930er Jahren von Louis Bergeron (1876–1948) für die Analyse der Ausbreitung von Oberflächenwellen auf Kanälen publiziert.[1]

Grundprinzip

Für rechteckige Signale mit „genügend“ steilen Flanken und „genügend“ langen und flachen Dächern, so dass der Einschwingvorgang innerhalb einer Phase abklingt, kann die Analyse von verlustlosen Leitungen bei speicherfreien Abschlüssen auf einen einfachen Schaltvorgang zurückgeführt werden. Dieser kann sowohl bei linearen als auch bei nichtlinearen Abschlüssen auf die Analyse nichtlinearer Gleichstromnetzwerke zurückgeführt werden. Die schrittweise grafische Lösung ist durch Finden der Arbeitspunkte für die einzelnen Zeitabschnitte von je einer Leitungslaufzeit τ als Schnittpunkt zwischen zwei Kennlinien möglich.

Für nichtlineare Abschlüsse gilt nicht der Überlagerungssatz, welcher auch nicht für die grafische Lösung benötigt wird. Deshalb haben Begriffe aus der linearen Leitungstheorie, wie beispielsweise der Reflexionsfaktor, bei nichtlinearen Abschlüssen keine Bedeutung.

Leitungstheoretischer Ausgangspunkt

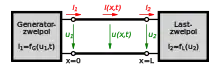
Für das Bergeron-Verfahren angenommene Leitungsstruktur

Die Leitungstheorie stellt mit den Definitionen für den (reellen) Wellenwiderstand

Z={\sqrt {\frac {L'}{C'}}}

und die (konstante) Phasengeschwindigkeit

v_{0}={\frac {1}{\sqrt {L'\cdot C'}}}

die allgemeine Lösung der Leitungsgleichungen der verlustlosen Leitung bereit:

u(x,t)=u_{h}\left(t-{\frac {x}{v_{0}}}\right)+u_{r}\left(t+{\frac {x}{v_{0}}}\right)

i(x,t)={\frac {1}{Z}}\cdot \left(u_{h}\left(t-{\frac {x}{v_{0}}}\right)-u_{r}\left(t+{\frac {x}{v_{0}}}\right)\right)

Dabei stellen $u_{h}$ und $u_{r}$ die vorlaufende bzw. zurücklaufende Welle dar. Beide bestehen in unserem Fall aus idealen Schaltflanken, welche die Leitung der Länge L ohne Dämpfung und Verzerrung in der Zeit

\tau ={\frac {v_{0}}{L}}

durchlaufen.

Die dynamischen Kennlinien der Leitung

Gesamtspannung und Gesamtstrom bestimmen sowohl die vor- als auch die rücklaufende (Spannungs-)Welle eindeutig, denn aus der allgemeinen Lösung ergibt sich

u_{h}\left(t-{\frac {x}{v_{0}}}\right)={\frac {u(x,t)+Z\cdot i(x,t)}{2}}

u_{r}\left(t+{\frac {x}{v_{0}}}\right)={\frac {u(x,t)-Z\cdot i(x,t)}{2}}

Direkt nach einem Schaltvorgang am Eingang ist die rücklaufende Welle für mindestens 2·τ stabil, weil die Schaltflanke erst nach der doppelten Laufzeit der Leitung wieder am Eingang wirken kann. Für diese ergibt sich aus vorstehender Gleichung

u_{r}\left(t\right)={\frac {u(0,t)-Z\cdot i(0,t)}{2}}

oder umgeformt

u(0,t)-Z\cdot i(0,t)=2\cdot u_{r}\left(t\right)

Das ist die Gleichung eines aktiver Zweipols, welche die „Leitung von Anfang her gesehen“ beschreibt. Wesentlich ist, dass der Innenwiderstand des Zweipols mit dem Wellenwiderstand der Leitung identisch und unabhängig von deren Abschluss ist.

Ähnliches gilt für einen Schaltvorgang am Ende:

u_{h}\left(t-{\frac {L}{v_{0}}}\right)={\frac {u(L,t)+Z\cdot i(L,t)}{2}}

woraus sich die „dynamische Gleichung der Leitung vom Ende her“ ergibt:

u(L,t)+Z\cdot i(L,t)=2\cdot u_{h}\left(t-{\frac {L}{v_{0}}}\right)

Das ist ebenfalls die Gleichung eines aktiven Zweipols, welche die „Leitung von Ende her gesehen“ beschreibt. Der Innenwiderstand dieses Zweipols ist mit dem (wegen der umgekehrten Stromrichtung) negativen Wellenwiderstand der Leitung identisch.

Diese „linearen dynamischen Kennlinien der Leitung“ sind nicht nur im nachfolgend beschriebenen Verfahren, sondern auch für Berechnungen des Schaltverhaltens von verlustlosen Leitungen bei Abschlüssen mit Speicherverhalten nutzbar.

Das Bergeron-Verfahren

Der Anfangszustand

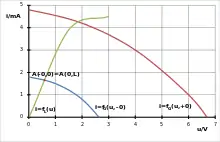
„Leeres“ Bergeron-Diagramm zur Zeit t<0

In das zu konstruierende Bergeron-Diagramm mit kartesischen Koordinatenachsen für Spannung und Strom werden zuerst die beiden Kennlinien des Generatorzweipols vor dem Schaltvorgang $i=f_{G}(u,-0)$ (im Diagramm blau dargestellt) und nach dem Schaltvorgang $i=f_{G}(u,+0)$ (im Diagramm braun dargestellt) sowie die Kennlinie des Lastzweipols $i=f_{L}(u)$ (im Diagramm grün dargestellt) eingetragen. Bei Bedarf können noch zwei Hilfslinien durch den 0-Punkt gezeichnet werden, deren Anstiege durch den positiven bzw. negativen Wellenwiderstand bestimmt werden (was im angeführten Beispiel nicht getan wurde). Sie könnten in den folgenden Schritten als Hilfe zur Parallelverschiebung dienen.

Vor dem zum Zeitpunkt $t=0$ stattfindenden Schaltvorgang befinden sich die Leitung und ihre Abschlüsse im gleichstrommäßig eingeschwungenen Zustand. Die verlustlose Leitung hat dabei keine Wirkung und der Arbeitspunkt – im Folgenden immer als A(Zeit,Ort) bezeichnet – am Leitungsanfang A(−0,0) ist gleich dem Arbeitspunkt am Leitungsende A(0,L). Er lässt sich einfach als Schnittpunkt der Kennlinien von Generatorzweipol (vor dem Schaltvorgang) und Lastzweipol ermitteln.

Der Schaltvorgang

Bergeron-Diagramm direkt nach dem Schaltvorgang zur Zeit t=+0

Zum Zeitpunkt $t=0$ ändert sich die Kennlinie des Generatorzweipols sprunghaft. Da die rücklaufende Welle konstant bleiben muss, ergibt sich der neue Arbeitspunkt A(+0,0) am Leitungsanfang als Schnittpunkt der neuen Generatorkennlinie $i=f_{G}(u,+0)$ und der „dynamischen Kennlinie der Leitung vom Anfang her gesehen“. Da diese auch durch den alten Arbeitspunkt $i=f_{G}(u,-0)$ gehen muss und ihr Anstieg durch den Wellenwiderstand $Z_{0}$ (im angeführten Beispiel 10 kΩ) bestimmt wird, lässt sie sich eindeutig konstruieren (im Diagramm rot dargestellt) und damit der Schnittpunkt A(+0,0) finden. Weil die rücklaufende Welle für mindestens zwei Leitungslaufzeiten $2\tau$ konstant ist, ändert sich nur der Wert der hinlaufenden Welle sprunghaft und die entstehende Flanke läuft mit der Geschwindigkeit $v_{0}$ zum Leitungsende.

Die Reflexion am Ende

Bergeron-Diagramm zur Zeit t=τ

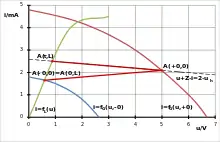
Wenn diese (oder eine später entstehende) Flanke am Ende ankommt, muss sich dort ebenfalls ein neuer Arbeitspunkt A(τ,L), allgemein A((2i+1)·τ,L), einstellen. Dazu wird die „dynamische Kennlinie der Leitung vom Ende her gesehen“ durch den letzten Arbeitspunkt am Anfang und mit dem durch den „negativen Wellenwiderstand“ bestimmten Anstieg gezeichnet. Ihr Schnittpunkt mit der Kennlinie des Lastzweipols $i=f_{L}(u)$ ergibt den neuen Arbeitspunkt am Leitungsende. Weil dort die hinlaufende Welle für zwei Leitungslaufzeiten konstant ist, kann sich nur der Wert der rücklaufenden Welle sprunghaft ändern und die entstehende Flanke läuft mit der Geschwindigkeit $v_{0}$ zurück zum Leitungsanfang.

Die Reflexion am Anfang

Bergeron-Diagramm zur Zeit t=2τ

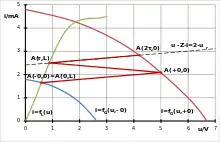
Wenn die am Leitungsende entstandene Flanke wieder am Leitungsanfang ankommt, muss sich dort wiederum ein neuer Arbeitspunkt A(2τ,0), allgemein A(2i·τ,0), einstellen. Dazu wird die „dynamische Kennlinie der Leitung vom Anfang her gesehen“ durch den letzten Arbeitspunkt am Ende und mit dem durch den (jetzt „positiven“) Wellenwiderstand bestimmten Anstieg gezeichnet. Ihr Schnittpunkt mit der Kennlinie des Generatorzweipols ergibt den neuen Arbeitspunkt am Leitungsanfang. Wieder ändert sich der Wert der rücklaufenden Welle sprunghaft und die entstehende Flanke läuft erneut mit der Geschwindigkeit $v_{0}$ zum Leitungsende.

Bergeron-Diagramm zur Zeit t=7τ

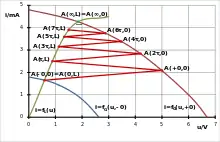
Beide vorstehenden Prozeduren werden mehrfach ausgeführt. Außer in speziellen Fällen wiederholen sich die Reflexionen unendlich oft und konvergieren im Schnittpunkt der Kennlinien von Generator- und Lastzweipol A(∞,0)=A(∞,L). Dieser stellt den stationären Arbeitspunkt nach dem Einschwingvorgang dar. Praktisch wird die Konstruktion beendet, wenn die gewünschte oder die Ablesegenauigkeit erreicht ist.

Zeitabläufe

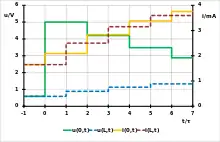
Aus dem Bergeron-Diagramm „abgelesener“ Zeitverlauf von Spannung und Strom am Anfang und Ende einer verlustlosen Leitung

Aus dem fertigen Bergeron-Diagramm lassen sich bei Bedarf die Werte von Spannung und Strom am Anfang und am Ende der Leitung zu geraden bzw. ungeraden Vielfachen der Laufzeit τ entnehmen und als (normierter) zeitlicher Ablauf darstellen.

Beispiel für einen Schaltvorgang zwischen TTL-Schaltkreisen

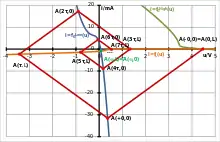
Bergeron-Diagramm für eine Leitung zwischen TTL-Gattern bei einer High-low-Flanke

Ein typischer Anwendungsfall des Bergeron-Verfahrens ist die Untersuchung der Übertragung von Impulsen auf „nicht sauber angepassten“ Leitungen zwischen digitalen Schaltkreisen. In diesem Beispiel wird die high/low-Flanke am Ausgang eines Standard-TTL-Gatters, welches über eine Leitung mit Z = 120 Ω den Eingang eines Standardgatters (ohne „Clampingdiode“) treibt, betrachtet. Die Kennlinien entsprechen näherungsweise den tatsächlichen, die Konstruktion wurde nach den oben dargelegten Schritten ausgeführt und bezeichnet.

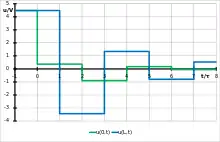
Verlauf der Spannung an einer Leitung zwischen TTL-Gattern bei einer High-low-Flanke

Aus dem entstehenden Bergeron-Diagramm lässt sich der Verlauf der Spannung am Eingang und Ausgang der Leitung (also am Ausgang bzw. Eingang des TTL-Gatters) „ablesen“. Man erkennt das starke negative Überschwingen der Spannung am Ausgang der Leitung, was eventuell zum Zerstören des folgenden Schaltkreises führen kann und in der Weiterentwicklung der Schaltkreise durch Einbau einer Clampingdiode vermieden wurde.

Siehe auch

Wellenfahrplan

Literatur

Wolfgang Hilberg: Impulse auf Leitungen. R. Oldenbourg Verlag GmbH, München 1981, ISBN 3-486-25491-X.
Hans-Georg Unger: Elektromagnetische Wellen auf Leitungen. Dr. Alfred Hüthig Verlag, Heidelberg 1980, ISBN 3-7785-0601-3.
Eberhard Kühn, Horst Schmied: Integrierte Schaltkreise. Verlag Technik, Berlin 1974.

Weblinks

Texas Instruments: The Bergeron Method – A Graphic Method for Determining Line Reflections in Transient Phenomena (PDF vom Oktober 1996). Abgerufen am 18. Januar 2014.

Einzelnachweise

M. Louis Bergeron: Methode Graphique Generale De Calcul Des Propagations D’ondes Planes. In: Bulletin de juillet-août. Extrait des Mémoires de la Société des Ingénieurs Civils de France, 1937.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] M. Louis Bergeron: Methode Graphique Generale De Calcul Des Propagations D’ondes Planes. In: Bulletin de juillet-août. Extrait des Mémoires de la Société des Ingénieurs Civils de France, 1937.