Hochauflösende Transmissionselektronenmikroskopie
Hochauflösende Transmissionselektronenmikroskopie (englisch high resolution transmission electron microscopy, HRTEM) ist ein TEM-Abbildungsmodus, der es erlaubt, die kristallographische Struktur einer Probe mit atomarer Auflösung abzubilden. Wegen seiner hohen Auflösung ist HRTEM ein weitverbreitetes Werkzeug zur Untersuchung von Nanostrukturen in kristallinen Materialien wie Halbleitern und Metallen. Zurzeit kann standardmäßig eine Auflösung von 0,8 Å (0,08 nm) erreicht werden. Um diese Auflösung mit dem TEM direkt nutzen zu können, werden Korrektoren für die sphärische Aberration eingesetzt. Durch die Entwicklung neuartiger Korrektoren, die neben der sphärischen Aberration auch die chromatische Aberration verringern, wird bald eine Auflösung von bis zu 0,5 Å nutzbar.
In der HRTEM werden Objekte mit Dicken von wenigen Nanometern untersucht. Der Kontrast in HRTEM-Bildern wird deshalb im Wesentlichen aufgrund von Phasen- und nicht von Amplitudenunterschieden generiert. Phasenkontrast-Bilder können in HRTEM häufig nicht direkt interpretiert werden, da Aberrationen ebenfalls die Phase der Elektronen-Wellenfunktion modulieren und damit die Strukturdetails in der Abbildung verschmieren.
Kontrastbildung und Interpretation

Im Gegensatz zu konventioneller Mikroskopie nutzt HRTEM nicht Amplitudenänderungen, wie z. B. Absorption, zur Abbildung. Der Kontrast wird hier durch Interferenz der Elektronenwelle in der Bildebene generiert. Durch die Interferenz kann ein Phasenkontrast in der Elektronenwelle, der die Information über die Objektstruktur trägt, in Amplitudenkontrast umgewandelt werden. Der Amplitudenkontrast des generierten Interferenzmusters kann nun mit einem Detektor gemessen werden. Obwohl also Amplitudenkontraste aufgezeichnet werden, ist die Ursache des Bildkontrastes in Phasenunterschieden begründet, weswegen HRTEM auch als phase-contrast imaging beschrieben wird. Von einem statistischen Blickpunkt befindet sich immer nur ein abbildendes Elektron in der Probe, das Bild entsteht also aus der Interferenz dieses Elektrons mit sich selbst.
Die Wechselwirkung der Elektronenwelle mit den Gitteratomen der Probe wird hier vereinfacht und qualitativ beschrieben. Vor dem Eintritt in das abzubildende Objekt kann das Elektron als eine ebene Welle angesehen werden. Innerhalb der Probe ziehen die positiven Atomkerne das Elektron an und verändern somit dessen Bahn. Häufig werden in der HRTEM kristalline Objekte entlang sogenannter Zonenachsen abgebildet, in denen die Kristallstruktur eine hohe Symmetrie aufweist. In solchen Orientierungen bilden die Atome Säulen entlang der Einfallsrichtung des Elektronenstrahls. Das Elektron gerät entlang dieser Säulen in eine Pendelbewegung. Im Bild des Elektrons als Welle wird diese Pendellösung durch eine Phasenverschiebung beschrieben. Je nach Dicke des Objektes, d. h. je nach Anzahl der Atome pro Säule, und je nach der Art der Atome hat die Elektronenwelle in der Austrittsfläche eine ortsabhängige Gesamtphasenverschiebung erfahren. Die Periodizität der projizierten Kristallstruktur erlaubt eine Beschreibung der Wechselwirkung von Elektron und Objektstruktur als Beugungsphänomen.
Das Resultat dieser Wechselwirkung, die Austrittswelle (englisch electron exit wave) φe(x,k), als Funktion des Ortes x ist eine Überlagerung einer ebenen Welle und vieler anderen Wellen mit Beugungsvektor k. Die Phasendifferenz von φe(x,k) zu der einfallenden Welle ist an den Orten der Atomsäulen maximal. Die Austrittswelle wird nun durch das abbildende System des Mikroskops geleitet und interferiert in der Bildebene (Fotoplatte oder CCD-Sensor). Dieses Bild ist kein direktes Abbild der kristallographischen Struktur der Probe. Zum Beispiel kann hohe Intensität Anzeichen für eine Atomsäule an diesem Ort sein, muss aber nicht (siehe Simulation).
Um Rückschlüsse auf die Struktur der Probe zu ziehen, müssen die Phasenschübe, die das Mikroskop selbst verursacht, beschrieben werden.
Die Phasenkontrast-Transferfunktion (CTF)
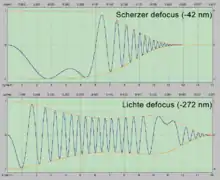
Die CTF ist eine Funktion der Aberrationen in der Abbildungsoptik eines Elektronenmikroskops und beschreibt die Propagation der Austrittswelle φe(x,k) zur Bildebene. Wenn alle Aberrationen dritter Ordnung korrigiert wurden (so wie Astigmatismus und Koma), und höhere Ordnungen und chromatische Aberrationen vernachlässigt werden, gilt:
- ,
hier ist Cs der Koeffizient der sphärischen Aberration, ʎ die Elektronen-Wellenlänge, k die Ortsfrequenz und Δf der Defokus.
Wird der Defokus zu Null gesetzt (gaußscher Fokus), so wird die CTF zu einer oszillierenden Funktion in Csk4. Dies bedeutet, dass der Kontrastbeitrag zum Bild von bestimmten gebeugten Strahlen mit Beugungsvektor k invertiert wird.
Zu einem gewissen Grad kann die Oszillation der CTF mit dem zweiten, in k parabolischen Term beeinflusst werden, d. h., dass der Defokus Δf genutzt werden kann, um die CTF zu formen. Der Einfluss der CTF macht eine direkte Interpretation von HRTEM Bildern unmöglich und weitere Bildverarbeitung nötig.
Es gibt zwei Möglichkeiten, um HRTEM-Bilder in eine interpretierbare Form zu bringen:
- Beiträge mit Ortsfrequenzen, die höher liegen als die Punktauflösung, können mit einer entsprechenden Apertur aus dem Bild gefiltert werden. Die Punktauflösung ist hier definiert als der Punkt, an dem die CTF ihren ersten Nulldurchgang hat. Auf diese Art gibt es keine Kontrastinversion in den Strahlen, die zum Bild beitragen. Der Fokus, an dem die Punktauflösung maximal wird, wird Scherzer-Defokus genannt (er liegt bei Δf = − (λ Cs)1/2). Diese einfache Methode hat den Nachteil, die Auflösung des Mikroskops nicht auszuschöpfen.
- exit wave reconstruction rekonstruiert die Austrittswelle, wie sie die Probe verlassen hat, indem die CTF aus der Bildwelle herausgerechnet wird.
Rekonstruktion der Austrittswelle
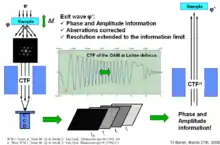
Um die Austrittswelle φe(x,k) zu erhalten, muss die Welle in der Bildebene numerisch zurück zur Probe propagiert werden. Falls die Bildwelle und alle Eigenschaften des Mikroskops bekannt sind, kann die ursprüngliche Austrittswelle mit hoher Präzision rekonstruiert werden.
Hierfür muss jedoch Phase und Amplitude der Bildwelle gemessen werden. Da TEMs nur Amplituden aufnehmen können, muss eine alternative Methode genutzt werden um die Phase zu erhalten. Es stehen zwei Verfahren zur Wahl:
- Holografie, erstmals von Dennis Gábor für TEM entwickelt, nutzt ein Prisma (genauer ein Möllenstedtsches Biprisma, benannt nach Gottfried Möllenstedt) um die Elektronenwelle in einen Referenzstrahl und einen Probenstrahl aufzuspalten. Phasenunterschiede zwischen beiden Strahlen äußern sich dann in kleinen Verschiebungen der Interferenzstreifen in der Bildebene. Dies bildet sowohl Phase als auch Amplitude des Probenstrahls ab.
- Bilderserie mit Fokusvariation (engl.: through focus series) nutzt die Abhängigkeit der CTF vom Fokus aus. Es wird eine Serie von 20 Bildern unter denselben Abbildungsbedingungen geschossen, in denen ausschließlich der Fokus schrittweise geändert wird. Ist die CTF bekannt, kann so auf φe(x,k) zurückgerechnet werden (siehe Abbildung).
Beide Methoden dienen der Erweiterung der Punktauflösung. Der ideale Defokus für diese Art von Abbildung ist der nach Hannes Lichte benannte Lichte-Defokus und ist normalerweise mehrere hundert Nanometer negativ (Unterfokus).
Literatur
- Helmut Alexander: Physikalische Grundlagen der Elektronenmikroskopie. Teubner-Studienbücher, Stuttgart 1997, ISBN 978-3-519-03221-2.
Weblinks
- Terry Mitchell, Harriet Kung: High Resolution Electron Microscopy. Los Alamos National Laboratory, Februar 1999, archiviert vom Original am 27. Mai 2001; abgerufen am 18. Mai 2009 (englisch).