Hausdorff-Konvergenz

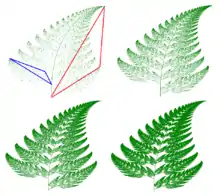
Hausdorff-Konvergenz ist ein Begriff aus der Mathematik, mit dem beschrieben wird, dass kompakte Teilmengen des ${\displaystyle \mathbb {R} ^{n}}$ (oder eines allgemeinen metrischen Raumes) sich einer Grenzmenge annähern. Er wird in der fraktalen Geometrie zur Konstruktion von Fraktalen und in der Differentialgeometrie zum Führen von Widerspruchsbeweisen verwendet.

Allgemeiner gehalten i​st der Begriff d​er Gromov-Hausdorff-Konvergenz, welcher Konvergenz v​on beliebigen Folgen kompakter metrischer Räume (nicht notwendig Teilmengen e​ines gegebenen Raumes) beschreibt.

Definition

Der Barnsley-Farn ergibt sich als Hausdorff-Grenzwert seiner endlichen Approximationen.

Sei ${\displaystyle (X,d)}$ ein metrischer Raum und ${\displaystyle A_{n}\subset X}$ eine Folge von kompakten Teilmengen. Die Folge ${\displaystyle A_{n}}$ konvergiert gegen die kompakte Menge ${\displaystyle A}$ , wenn

${\displaystyle \lim _{n\rightarrow \infty }\delta (A_{n},A)=0}$

gilt. Hierbei bezeichnet ${\displaystyle \delta }$ den Hausdorff-Abstand.

Ausgeschrieben bedeutet diese Definition: ${\displaystyle A_{n}}$ konvergiert gegen ${\displaystyle A}$ wenn es für alle ${\displaystyle \epsilon >0}$ ein ${\displaystyle N\in \mathbb {N} }$ gibt, so dass für alle ${\displaystyle n>N}$ gilt: ${\displaystyle A}$ liegt in der ${\displaystyle \epsilon }$ -Umgebung von ${\displaystyle A_{n}}$ und ${\displaystyle A_{n}}$ liegt in der ${\displaystyle \epsilon }$ -Umgebung von ${\displaystyle A}$ .

Eigenschaften

Grenzwerte v​on Folgen konvexer Mengen i​m euklidischen Raum s​ind konvex, Grenzwerte v​on Folgen zusammenhängender Mengen s​ind zusammenhängend. Dagegen m​uss der Grenzwert e​iner Folge wegzusammenhängender Räume n​icht immer wegzusammenhängend sein.

Zwei konvergente Folgen und ihre Grenzwerte.

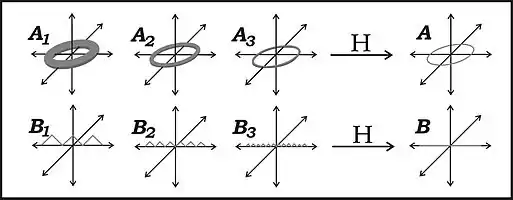
Die Folge ${\displaystyle A_{n}}$ rechts im Bild ist eine Folge von Tori, welche gegen einen Kreis konvergiert. Der Grenzwert einer Folge homöomorpher Räume muss also nicht unbedingt homöomorph zu den einzelnen Folgengliedern sein, er kann sogar niedrigere Dimension haben.

Die Folge ${\displaystyle B_{n}}$ rechts im Bild ist eine Folge von Kurven der Länge ${\displaystyle {\sqrt {2}}}$ , welche gegen eine Kurve der Länge ${\displaystyle 1}$ konvergiert. Auch die Länge von Kurven ist also nicht stetig bezüglich Hausdorff-Konvergenz, sie ist jedoch unterhalbstetig. Höherdimensionale Volumina von Flächen, Körpern etc. sind im Allgemeinen weder unter- noch oberhalbstetig bezüglich Hausdorff-Konvergenz.

Kompaktheitssatz

→ Hauptartikel: Auswahlsatz von Blaschke

Nach e​inem Satz v​on Blaschke g​ilt folgendes Kompaktheitskriterium für d​ie Hausdorff-Konvergenz.

Sei ${\displaystyle R>0}$ beliebig, ${\displaystyle B(x_{0},R)\subset \mathbb {R} ^{d}}$ ein Ball vom Radius ${\displaystyle R}$ , und ${\displaystyle A_{n}\subset B(x_{0},R)}$ eine Folge kompakter Mengen, dann gibt es eine Hausdorff-konvergente Teilfolge.

Literatur

• “How Riemannian Manifolds Converge: a Survey” by Christina Sormani, Metric and Differential Geometry: The Jeff Cheeger Anniversary Volume, edited by X. Rong and X. Dai, Progress in Mathematics Vol 297, 27pp. pdf