Hénon-Abbildung

Der französische Astronom Michel Hénon fand die folgende zweidimensionale Abbildung, die sogenannte Hénon-Abbildung, die aus einer Vereinfachung der zur Lorenz-Gleichung gehörenden Poincaré-Abbildung hergeleitet wurde. Die Lorenz-Gleichung stammte ursprünglich aus der Meteorologie und war eines der ersten dynamischen Systeme, in denen man chaotisches Verhalten gefunden hat. Die Hénon-Abbildung wird beschrieben durch:[1]

${\begin{matrix}x_{n+1}=1+y_{n}-ax_{n}^{2}\\y_{n+1}=bx_{n}\end{matrix}}$

Hénon-Abbildung für die Parameter a=1,4 und b=0,3: hufeisenförmiges Gebilde

mit $a>0,0\leq b\leq 1$ . Hierbei sind a und b die Kontrollparamenter des Systems.

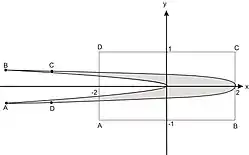
Die Hénon-Abbildung setzt sich aus insgesamt drei Elementarabbildungen $Abb_{k}$ mit k=1,2,3 zusammen:[1]

nichtlineare Verbiegung der y-Koordinate: $Abb_{1}(x,y)=(x,1+y+ax^{2})$ ,
Kontraktion der x-Koordinate: $Abb_{2}(x,y)=(bx,y)$ für 0<b<1,
Spiegelung an der Hauptdiagonalen y=x: $Abb_{3}(x,y)=(y,x)$ .

Es sei noch erwähnt, dass eine weitere wichtige Eigenschaft dieser Abbildung die Selbstähnlichkeit ist. In einfachen Worten ausgedrückt versteht man darunter eine fraktale Vergrößerung eines beliebigen Teilbereichs, der wieder seinem Anfangsobjekt ähnlich ist. Der Attraktor der Hénon-Abbildung ist ein seltsamer Attraktor.

Einzelnachweise

Kenneth J. Falconer: Fraktale Geometrie – Mathematische Grundlagen und Anwendungen. Spektrum Akademischer Verlag, 1993, ISBN 3-86025-075-2, S. 207–209.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[falconer1993-1] Kenneth J. Falconer: Fraktale Geometrie – Mathematische Grundlagen und Anwendungen. Spektrum Akademischer Verlag, 1993, ISBN 3-86025-075-2, S. 207–209.