Brüsselator

Der Brüsselator ist ein einfaches Modell zur Beschreibung chemischer Oszillatoren. Der Brüsselator wurde von Ilya Prigogine und René Lefever an der Université Libre de Bruxelles in Belgien entwickelt, daher auch der Name.

Beschreibung

Lösung des Brüsselators für verschiedene Randbedingungen, zusammen mit Phasenraumplots. Oben ergeben sich stabile Oszillationen, während im unteren Fall die Lösungen einem Fixpunkt zustreben.

Vier hypothetische Reaktionsgleichungen bilden ein einfaches Modell, das alle Phänomene von chemischen Oszillatoren (wie der Belousov-Zhabotinsky-Reaktion) widerspiegelt.[1] Ein ähnliches Modellsystem wurde 1985 an der Humboldt-Universität zu Berlin durch Vereinfachung aus einem real existierenden Reaktionssystem abgeleitet.[2]

I	A	→	X
II	B + X	→	Y + C
III	2X + Y	→	3X	(autokatalytisch)
IV	X	→	D

Σ (I-IV je einmal)	A + B	→	C + D

Die Reaktionsgeschwindigkeiten werden durch die Konstanten k₁ bis k₄ widergespiegelt, die Konzentrationen von A und von B konstant gehalten, und die Produkte C und D ständig abgeführt.

Die Konzentrationen von X und von Y reagieren empfindlich auf kleine Störungen und erreichen schnell einen oszillierenden Zustand, wenn die Gesamtreaktion weit vom Gleichgewichtszustand entfernt ist. Man hat also ein thermodynamisch offenes System und kann zwei Ratengleichungen für die Konzentration von X und von Y aufstellen:

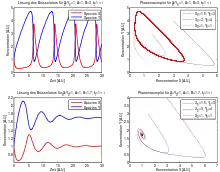
{\begin{alignedat}{2}&{\frac {\mathrm {d} X}{\mathrm {d} t}}=k_{1}A-&&k_{2}BX+k_{3}X^{2}Y-k_{4}X\\&{\frac {\mathrm {d} Y}{\mathrm {d} t}}=&&k_{2}BX-k_{3}X^{2}Y\end{alignedat}}

Diese Differentialgleichungen können numerisch gelöst werden. Nebenstehende Abbildung zeigt einige Lösungen. Je nach Wahl der freien Parameter k₁A, k₂B, k₃ und k₄ ergibt sich unterschiedliches Verhalten: im oberen Fall sieht man stabile Oszillationen, während im unteren Fall bei anderer Wahl der Parameter die Konzentrationen X(t) und Y(t) einem Fixpunkt im Phasenraum zustreben.

Stabilitätsbetrachtung

Wie oben gezeigt, hat der Brüsselator je nach Parametrisierung stabile Oszillationen als Lösung oder strebt im Phasenraum einem Fixpunkt zu.

Dieser Fixpunkt ergibt sich über

{\frac {\mathrm {d} X}{\mathrm {d} t}}={\frac {\mathrm {d} Y}{\mathrm {d} t}}=0

zu:[3]

{\begin{alignedat}{2}\Rightarrow &X={\frac {k_{1}}{k_{4}}}&&\cdot A\\&Y={\frac {k_{4}\,k_{2}}{k_{3}\,k_{1}}}&&\cdot {\frac {B}{A}}\end{alignedat}}

Mit Hilfe der linearen Stabilitätsanalyse lässt sich weiter zeigen, dass dieser Fixpunkt instabil wird, wenn gilt:[3]

B>{\frac {k_{4}}{k_{2}}}+{\frac {k_{3}}{k_{2}}}\cdot \left({\frac {k_{1}}{k_{4}}}\cdot A\right)^{2}

In diesem Fall streben die Trajektorien $(X(t),Y(t))$ einem Grenzzyklus im Phasenraum zu, und das System führt die gezeigten Oszillationen aus.

Als Reaktions-Diffusions-Modell

Ein Zeit- und raumabhängiger zellulärer Automat des Brüsselators mit zwei Quellenpunken und periodischen Randbedingungen. Es entstehen kreisförmige Wellen und Spiralwellen.

Man kann das Modell auch auf ein Reaktions-Diffusions-Modell erweitern und erhält dann bei Wahl der richtigen Parameter Chemische Wellen als Lösung, wie rechts gezeigt.

Die Differentialgleichungen werden um einen Diffusionsanteil $D_{X}\cdot \nabla ^{2}X({\vec {x}},t)$ bzw. $D_{Y}\cdot \nabla ^{2}Y({\vec {x}},t)$ erweitert und lauten dann:[3]

{\begin{alignedat}{3}&{\frac {\partial X({\vec {x}},t)}{\partial t}}=k_{1}A&&-k_{2}BX({\vec {x}},t)+k_{3}X^{2}({\vec {x}},t)Y({\vec {x}},t)-k_{4}X({\vec {x}},t)&&&+D_{X}\cdot \nabla ^{2}X({\vec {x}},t)\\&{\frac {\partial Y({\vec {x}},t)}{\partial t}}=&&+k_{2}BX({\vec {x}},t)-k_{3}X^{2}({\vec {x}},t)Y({\vec {x}},t)&&&+D_{Y}\cdot \nabla ^{2}Y({\vec {x}},t)\end{alignedat}}

Hierin ist

${\vec {x}}$ ein Punkt im Raum
$D$ der Diffusionskoeffizient
$\nabla ^{2}$ der Laplace-Operator, also in kartesischen Koordinaten die Summe der zweiten räumlichen Ableitungen.

Literatur

Dilip Kondepudi, Ilya Prigogine: Modern Thermodynamics. From Heat Engines to Dissipative Structures. John Wiley & Sons, Weinheim, New York 1998.

Einzelnachweise

R. J. Field: Eine oszillierende Reaktion. In: Chemie in unserer Zeit, 7. Jahrg 1973, Nr. 6, S. 171–176, doi:10.1002/ciuz.19730070603.
K. Bar-Eli: The minimal bromate oscillator simplified, J. Phys. Chem., 1985, doi:10.1021/j100259a030.
Dilip Kondepudi, Ilya Prigogine: Modern Thermodynamics. From Heat Engines to Dissipative Structures. John Wiley & Sons, Chichester u. a. 1998, ISBN 0-471-97393-9.

Weblinks

Jan Krieger: Reaktions-Diffusions-Systeme (PDF; 2,5 MB), 2004.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] R. J. Field: Eine oszillierende Reaktion. In: Chemie in unserer Zeit, 7. Jahrg 1973, Nr. 6, S. 171–176, doi:10.1002/ciuz.19730070603.

[2] K. Bar-Eli: The minimal bromate oscillator simplified, J. Phys. Chem., 1985, doi:10.1021/j100259a030.

[KondepudiPrigogine1998-3] Dilip Kondepudi, Ilya Prigogine: Modern Thermodynamics. From Heat Engines to Dissipative Structures. John Wiley & Sons, Chichester u. a. 1998, ISBN 0-471-97393-9.