Sphärische Geometrie

Die sphärische Geometrie, auch Kugelgeometrie oder Geometrie auf der Kugel, befasst sich mit Punkten und Punktmengen auf der Kugel. Motiviert ist sie ursprünglich durch geometrische Betrachtungen auf der Erdkugel (vgl. Kartografie) und der Himmelssphäre (vgl. Astrometrie). Innerhalb der Geometrie ist sie besonders von Interesse, da sie bei geeigneter Definition des Punktes auf der Kugel sowohl ein Modell für die elliptische Geometrie darstellt als auch die Axiome der projektiven Geometrie erfüllt.

Die sphärische Geometrie unterscheidet sich in einigen Punkten stark von der ebenen euklidischen Geometrie. Sie besitzt keine Parallelen, da sich zwei Großkreise, das Analogon der Geraden auf der Kugel, stets schneiden. Viele aus der euklidischen Geometrie bekannte Sätze, wie die 180°-Winkelsumme im Dreieck oder der Satz des Pythagoras, haben auf der Kugel keine Gültigkeit. Es gibt sie allerdings in adaptierter Form.

Grundbegriffe

Die Ausgangsbegriffe ebener Geometrien sind der Punkt und die Gerade. Auf der Kugel werden diese folgendermaßen definiert:

Gerade

Die Rolle der Geraden kommt in der sphärischen Geometrie den Großkreisen zu. Großkreise sind Kreise auf der Kugel, deren (euklidischer) Mittelpunkt der Kugelmittelpunkt ist. Beispiele für Großkreise auf dem Globus sind der Äquator und die Meridiane. Einen Großkreis erhält man durch Schnitt der Kugeloberfläche mit einer den Kugelmittelpunkt enthaltenden Ebene.

Punkt

Durch Schnitt der Kugel mit einer euklidischen Ebene erhält man einen Kreis. Ist der Abstand des Mittelpunktes der Kugel zu der schneidenden Ebene gleich dem Radius der Kugel, so beschreibt der Schnitt gerade einen Kreis mit Radius 0, also einen Punkt auf der Kugel.

Geographischer Punkt

In der geographischen Auffassung von sphärischer Geometrie wird die Definition des Punktes aus der euklidischen Geometrie übernommen, d. h. die Menge der sphärischen Punkte wird definiert als die Menge aller Punkte des dreidimensionalen euklidischen Raums, die sich auf der Kugeloberfläche befinden.

Elliptischer Punkt

Vom geometrischen Standpunkt hat die geographische Definition des Punktes einen gravierenden Nachteil. In geometrischen Axiomensystemen wird im Allgemeinen gefordert, dass zwei Punkte genau eine Gerade bestimmen. Dies ist bei obiger Definition nicht der Fall, wenn man Gegenpunkte auf der Kugel betrachtet. Gegenpunkte sind Punkte, deren euklidische Verbindungsgerade durch den Kugelmittelpunkt verläuft. (Sie verhalten sich also zueinander wie Nord- und Südpol auf dem Globus.) Durch Gegenpunkte verlaufen unendlich viele Großkreise (entsprechend den Längenkreisen auf dem Globus). Jeder Großkreis durch einen Punkt verläuft auch durch seinen Gegenpunkt. Es ist deshalb sinnvoll, Paare von Gegenpunkten zu einem Punkt zusammenzufassen.

Da die elliptische Definition des Punktes jeden Punkt mit seinem Gegenpunkt identifiziert, wird auch jede Figur (Punktmenge) auf der Kugel mit ihrer Gegenfigur identifiziert. (Insbesondere besteht zum Beispiel ein Dreieck aus zwei Gegendreiecken.)

Strecke

Strecken sind auf der Kugel Großkreisbögen. Der Abstand zweier Punkte A und B auf der Kugel ist identisch mit der Länge des kürzesten Großkreisbogens von A nach B. An der Einheitskugel mit dem Mittelpunkt M ist dessen Länge mit dem Winkel $\angle AMB$ im Bogenmaß identisch. Auch auf einer Kugel mit beliebigem Radius r können Längen als Winkel angegeben werden. Die tatsächliche sphärische Länge d errechnet sich dann aus dem Winkel im Bogenmaß als $d=\angle AMB\cdot r$ .

Bei elliptischer Definition des Punktes entspricht der kleinere der beiden Winkel zwischen den die Gegenpunkte verbindenden euklidischen Geraden dem sphärischen Abstand auf der Einheitskugel. Der Abstand ist daher nie größer als $\pi /2$ .

Kreis

Durch Schnitt der Kugel mit einer euklidischen Ebene erhält man einen Kreis. In der sphärischen Geometrie sind also Geraden (Schnitte der Kugel mit euklidischen Ebenen, die den Kugelmittelpunkt enthalten) nichts anderes als besondere Kreise (Großkreise). Der Schnittkreis der Kugel mit einer Ebene, die den Kugelmittelpunkt nicht enthält, wird Kleinkreis genannt. (Auf dem Globus sind z. B. mit Ausnahme des Äquators alle Breitengrade Kleinkreise.)

Flächenberechnung

Kugelzweieck

Zwei Großkreise mit den Schnittpunkten P und P' unterteilen die Kugeloberfläche in vier Kugelzweiecke. Ein Kugelzweieck wird durch zwei P und P' verbindende Kreisbögen dieser Großkreise begrenzt. Die Fläche $A_{Z}$ eines Kugelzweiecks verhält sich zur Gesamtoberfläche der Kugel $A_{K}$ wie sein Öffnungswinkel $\alpha$ zum Vollwinkel:

A_{Z}={\frac {\alpha }{2\pi }}\cdot A_{K}={\frac {\alpha }{2\pi }}\cdot 4\pi r^{2}=2\alpha r^{2}

.

Insbesondere gilt also auf der Einheitskugel

A_{Z}=2\alpha

.

Kugeldreieck

Der Flächeninhalt $A_{D}$ eines Kugeldreiecks mit den Winkeln $\alpha ,\beta$ und $\gamma$ errechnet sich aus seinen Winkeln:

A_{D}=(\alpha +\beta +\gamma -\pi )\cdot r^{2}

Da der Flächeninhalt immer größer als Null ist, muss die Summe der drei Innenwinkel eines sphärischen Dreiecks größer als $\pi$ (oder 180°) sein:

\alpha +\beta +\gamma >\pi

Der Überschuss der Winkelsumme über die Winkelsumme eines euklidischen Dreiecks wird als sphärischer Exzess bezeichnet. Der sphärische Exzess eines Dreiecks ist zu dessen Flächeninhalt proportional (und auf der Einheitskugel mit dem Proportionalitätsfaktor 1 sogar gleich).

Die Kugel als projektive Ebene, Dualität und Polarität

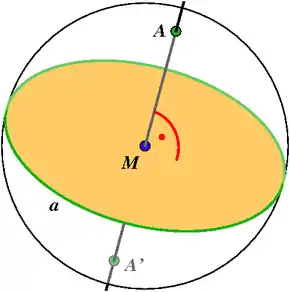
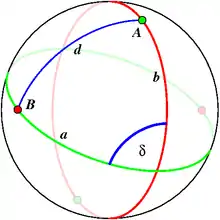
Dualität von Punkt und Gerade auf der Kugel

Inzidenz- und Winkel-Längen-Erhalt bei Dualisierung

Die sphärische Geometrie ist mit der elliptischen Definition der Punkte eine projektive Ebene. In der projektiven Geometrie lassen sich alle Sätze dualisieren, das heißt, die Begriffe Punkt und Gerade werden vertauscht (demzufolge auch Längen und Winkel wie in obiger Tabelle). Auf der Kugel lässt sich sogar jeder Geraden a ihr dualer Punkt A sowie umgekehrt jedem Punkt A seine duale Gerade a eindeutig zuweisen. Zu einem Kreis erhält man das duale Punktepaar als Schnittpunkte der Kugel mit der durch den Kugelmittelpunkt verlaufenden Senkrechten zur Ebene des Kreises (vgl. Abbildung).

Bei der Dualisierung bleibt die Inzidenz von Punkten und Geraden erhalten. Es gilt also: Wenn ein Punkt A auf einer Geraden b liegt, so verläuft die zu ihm duale Gerade a durch den zur Geraden b dualen Punkt B. Aber nicht nur die Inzidenz bleibt erhalten, sondern auch Winkel und Längen gehen ineinander über. Das Maß d des Winkels zwischen zwei Geraden a und b entspricht (auf der Einheitskugel) dem Maß des Abstands d zwischen den zu den Geraden dualen Punkten A und B.

→ Diese Dualität ist eine spezielle Korrelation und zwar eine elliptische, projektive Polarität. Dies wird im Artikel Korrelation (Projektive Geometrie) ausführlicher erläutert.

Koordinaten

Um ein Koordinatensystem zu erstellen, nimmt man zuerst willkürlich einen Großkreis als Äquator. Anschließend wählt man einen Meridian als Nullmeridian und legt einen Drehsinn fest. Nun kann man die Winkel vom Äquator und vom Nullmeridian aus messen und somit jede Position auf der Kugel eindeutig festlegen. Breitenkreise sind parallel zum Äquator, während Längenkreise durch die beiden Pole gehen.

Grenzfallregel

Bei Berechnungen auf der Kugeloberfläche gilt der Grundsatz, dass alle Formeln, welche den Kugelradius $r\,$ enthalten und daher die absolute Größe berücksichtigen, für den Grenzfall $r\to \infty$ in gültige Formeln der ebenen Geometrie übergehen müssen.

Siehe auch

Sphärische Trigonometrie
Orthodrome (kürzeste Entfernung auf der Kugel)

Weblinks

Commons: Sphärische Geometrie – Sammlung von Bildern, Videos und Audiodateien

Vorlesung über sphärische Geometrie

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.