ZHIT
ZHIT, auch ZHIT-Algorithmus oder ZHIT-Näherung, findet Anwendung in der elektrochemische Impedanzspektroskopie (EIS). Dort stellt sie eine Beziehung zwischen den beiden Messgrößen Modulus der Impedanz und Phasenverschiebung von Zweipol-Systemen in Form einer Integralgleichung her. Der ZHIT-Algorithmus erlaubt die Prüfung der Stationarität des Prüfobjekts sowie die Rückrechnung der Impedanzdaten aus den Phasendaten. Die Abkürzung „ZHIT“ steht für Zweipol-Hilbert-Transformation.
Motivation
Eine wichtige Anwendung des ZHIT ist die Überprüfung experimenteller Impedanzspektren auf Artefakte (siehe Artefakt (Technik)). Die Auswertung impedanzspektroskopischer Untersuchungen wird oft dadurch erschwert, dass sich die zu untersuchenden Objekte während der Messung verändern können. Dies trifft auf viele Standardanwendungen der elektrochemischen Impedanzspektroskopie zu, wie etwa die Untersuchung von Brennstoffzellen und Akkumulatoren unter Stromentnahme, die Untersuchung von lichtsensitiven Systemen unter Beleuchtung (z. B. Photo-Elektrochromie) oder die Untersuchung der Wasseraufnahme von Lacken auf Metalloberflächen (Korrosionsschutz). Ein anschauliches Beispiel für ein instationäres System ist ein Lithium-Ionen-Akkumulator während der Zyklisierung bzw. Entladung: durch die Stromentnahme ändert sich der Ladungszustand des Akkumulators und damit das System selbst, da die Änderung des Ladungszustands mit einer chemischen Redoxreaktion einhergeht und sich die Konzentration der daran beteiligten Substanzen ändert. Dies führt zur Verletzung von Stationarität und Kausalität, so dass Impedanzspektren solcher Systeme nach theoretischen Gesichtspunkten nicht auswertbar sind. Mit Hilfe des ZHIT-Algorithmus lassen sich solche und ähnliche Artefakte erkennen und gegebenenfalls kausale Spektren rekonstruieren, die konsistent mit den Kramers-Kronig-Beziehungen sind und dadurch ausgewertet werden können.
Mathematische Formulierung
ZHIT ist ein Spezialfall der Hilbert-Transformation und kann durch die Einschränkung der Kramers-Kronig-Beziehungen auf Zweipolsysteme abgeleitet werden. Die Beziehungen zwischen Impedanz und Phase können anschaulich aus dem Bodediagramm eines Impedanzspektrums abgeleitet werden. Man erhält Gleichung (1) als allgemeine Lösung des Zusammenhangs zwischen Modulus der Impedanz und der Phasenverschiebung[1][2].
Gleichung (1) besagt, dass man den Logarithmus der Impedanz () an einer Stelle bis auf einen konstanten Wert () berechnen kann, indem man die Phasenverschiebung bis zur interessierenden Stelle integriert, wobei der Startwert des Integrals beliebig gewählt werden kann. Als zusätzlichen Beitrag zur Berechnung von müssen noch die ungeraden Ableitung der Phasenverschiebung an der Stelle , gewichtet mit den Faktoren aufaddiert werden. Die Faktoren können gemäß Gleichung (2) berechnet werden, wobei die riemannsche ζ-Funktion bedeutet.
| 2 | ||
| 4 | ||
| 6 | ||
| 8 |
Zur ZHIT-Näherung wie sie in der Praxis angewandt wird, kommt man aus Gleichung (1) durch Beschränkung auf die erste Ableitung der Phasenverschiebung und Vernachlässigung der höheren Ableitungen (Gleichung (3)), wobei C eine Konstante repräsentiert.
Die freie Wählbarkeit der Integrationsgrenzen im ZHIT-Algorithmus ist ein fundamentaler Unterschied zu den Kramers-Kronig-Beziehungen; bei ihr sind die Integrationsgrenzen und . Der Vorteil der ZHIT resultiert daraus, dass beide Integrationsgrenzen innerhalb des gemessenen Spektrums gewählt werden können und nicht wie bei den Kramers-Kronig-Beziehungen gegen die (nicht realen) Frequenzen 0 und extrapoliert werden müssen.
Praktische Durchführung
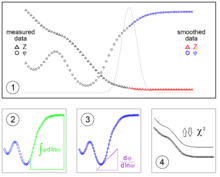
Die praktische Durchführung der ZHIT-Näherung ist in Abbildung 1 schematisch dargestellt. Aus den Messpunkten von Impedanz und Phase wird durch Glättung je ein kontinuierlicher Kurvenzug (Spline) für die beiden unabhängigen Messgrößen Impedanz und Phase erstellt (Teilbild (1)). Mit Hilfe des Splines für die Phasenverschiebung werden nun Funktionswerte für die Impedanz ermittelt. Zunächst wird die Phasenverschiebung bis zur entsprechenden Frequenz aufintegriert, wobei man zweckmäßigerweise als Startfrequenz die höchste interessierende Frequenz wählt (Teilbild (1)). Ebenfalls aus dem Spline der Phasenverschiebung lässt sich die Steigung der Phasenverschiebung an ermitteln (Teilbild(3)). Man erhält so einen rekonstruierten Kurvenzug für die Impedanz, der (im Idealfall) zur originalen Messkurve der Impedanz (nur) parallelverschoben ist. Zur Ermittlung der Konstanten C in der ZHIT-Gleichung (Teilbild (4)) gibt es mehrere Möglichkeiten. Eine Möglichkeit ist, dass man die Parallelverschiebung der rekonstruierten Impedanz in einem Frequenzbereich durchführt, die nicht durch das Auftreten von Artefakten beeinflusst ist (siehe Anmerkungen). Diese Verschiebung wird durch Lineare Regression vorgenommen. Durch Vergleich der nun resultierenden, rekonstruierten Impedanzkurve mit der original gemessenen (bzw. des Splines der Impedanz) können nun Artefakte detektiert werden. Diese befinden sich in aller Regel im hochfrequenten Bereich (verursacht durch Induktion bzw. Gegeninduktion, speziell bei niederohmigen Systemen) oder im tieffrequenten Bereich (verursacht durch die Veränderung des Systems während der Messung (=Drift)).
Anmerkungen (Zeitbedarf Impedanzmessung)
Die benötigte Messzeit für einen einzelnen Impedanzmesspunkt hängt sehr stark von der interessierenden Frequenz ab. Während Frequenzen oberhalb von etwa 1 Hz praktisch in Sekundenschnelle gemessen werden können, steigt die Messzeit im tieferfrequenten Bereich exponentiell an.
- Obwohl die genaue Dauer zur Messung eines kompletten Impedanzspektrums vom Messsystem selbst und internen Einstellungen abhängen, können folgende Messzeiten bei sequentieller Messung der Frequenzmesspunkte als Faustregeln angenommen werden, wobei die obere Frequenz zu 100 kHz oder 1 MHz angenommen wird.
- Bis ca. 1 Hz beträgt die Messzeit ca. 1 Minute, bis 0,1 Hz ca. 5 Minuten, bis 0,05 Hz ca. 10 Minuten, bis 0,02 Hz ca. 15 Minuten und bis 0,01 Hz ca. 30 Minuten.
- Messungen bis unter 0,01 Hz können mit Messzeiten im Bereich mehrerer Stunden verbunden sein.
- Als Konsequenz dieser Zeitabhängigkeit der Messung bei den unterschiedlichen Frequenzen kann man ein Spektrum grob in drei Teilbereiche einteilen, was das Auftreten von Artefakten betrifft: hochfrequent (ca. > 100 bis 1000 Hz) können Induktion bzw. Gegeninduktion dominieren. Tieffrequent (bei Frequenzen < 1 Hz) kann Drift durch merkliche Veränderung des Systems auftreten.
- Der Bereich zwischen etwa 1 Hz und 1000 Hz ist in der Regel weder von hochfrequenten noch tieffrequenten Artefakten beeinflusst, wobei man die Netzfrequenz (50 Hz) ebenfalls ausschließen muss.
Anmerkungen (Verfahren)
Neben der Rekonstruktion der Impedanz aus der Phasenverschiebung ist auch der umgekehrte Weg möglich.[2] Die hier beschriebene Vorgehensweise bietet jedoch mehrere Vorteile.
- Bei der Berechnung der Phasenverschiebung aus der Impedanz tritt anstelle der Konstanten C in Gleichung (3) eine Funktion der Kreisfrequenz ω auf, die schwieriger zu bestimmen ist
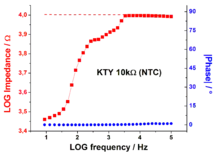 Abbildung 2: Impedanzmessung eines Temperatursensors KTY (10 KΩ), wobei der Sensor während der Messung erwärmt wurde
Abbildung 2: Impedanzmessung eines Temperatursensors KTY (10 KΩ), wobei der Sensor während der Messung erwärmt wurde - „Die Phasenverschiebung ist stabiler als die Impedanz.“ Hinter dieser Aussage verbirgt sich die Tatsache, dass für Impedanzelemente (genauer: constant phase elemente, CPE[4][5]) die Eigenschaft Phasenverschiebung konstant bleibt, auch wenn sich der Wert der Impedanz ändert. Solche CP-Elemente sind unter anderen die typischen elektronischen Elemente wie elektrischer Widerstand, Kondensator und Spule. Zur Veranschaulichung zeigt Abbildung 2 das Impedanzspektrums eines NTC-Widerstands, der während der Messung (beginnend zwischen 1 kHz und 10 kHz bis zu tiefen Frequenzen) erwärmt wurde. Man kann deutlich erkennen, dass sich der Wert der Impedanz (rote Kurve) mit der Temperatur ändert, während der Betrag der Phasenverschiebung (blaue Kurve) konstant bleibt („ein Widerstand bleibt ein Widerstand“).
- Die Rekonstruktion der Impedanz aus der Phasenverschiebung stellt weiterhin den „inneren (=komplexen)“ Zusammenhang zwischen diesen beiden Messgrößen wieder her. Dieser Zusammenhang geht durch die unabhängige Konstruktion der Stützpunktsplines für Impedanz und Phase (Abbildung 1) verloren. Je nach untersuchtem System kann dieser wiederhergestellte Zusammenhang – auch bei Abwesenheit von Artefakten – zu einer verbesserten Auswertung von Spektren führen. In solchen Fällen überwiegt der Genauigkeitsgewinn durch die Rekonstruktion der komplexen Impedanz den Approximationsfehler nach Gleichung (3), der durch die Vernachlässigung der höheren Ableitungen entsteht.
Anwendungen
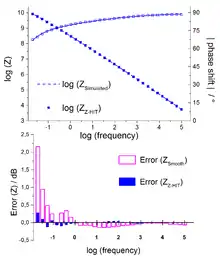
In Abbildung 3 ist ein Impedanzspektrum einer Messserie einer lackierten Stahlprobe während der Wasseraufnahme abgebildet[6] (oberes Teildiagramm). Die Symbole in dem Diagramm stellen die Stützstellen der Messung dar, während die durchgezogenen Linien die nach einem bestimmten Modell simulierten, theoretischen Werte darstellen. Die Stützstellen für die Impedanz wurden dabei durch die ZHIT Rekonstruktion aus der Phasenverschiebung gewonnen. Der untere Teil des Diagramms zeigt den normalisierten Fehler (ZZHIT − Zsmooth)/ZZHIT·100 der Impedanz der entsteht, wenn man die Messung mit dem Modell simuliert, wobei einmal die Stützpunkte der Impedanz aus den "gesplinten(=Zsmooth)" Messwerten selbst (magenta)- und ein zweitesmal mit den aus den nach dem ZHIT rekonstruierten (= ZZHIT)Impedanzwerten (blau) erstellt werden. Die Verbesserung durch die Verwendung der rekonstruierten Daten ist signifikant.
Anmerkung: Fehlerbilder wie im unteren Teildiagramm (magenta) können oft der Anlass sein, ein vorhandenes Modell für die Simulation mit zusätzlichen Elementen zu erweitern, um den Fehler zu minimieren. Das ist jedoch prinzipiell nicht möglich. Die Drift im Impedanzspektrum äußert sich im tieffrequenten Teil ja dadurch, dass sich das System während der Messung verändert. Das Spektrum in Abbildung 3 kommt dadurch zustande, dass Wasser in die Poren eindringt. Dies vermindert die Impedanz (Widerstand) der Beschichtung. De facto verhält sich das System während der Wasseraufnahme so, als ob bei jedem tieffrequenten Messpunkt der Widerstand der Beschichtung durch einen anderen, kleineren Widerstand ersetzt worden wäre. Es gibt aber kein Impedanzelement, das so ein Verhalten zeigt. Jede Erweiterung des Modells würde daher nur dazu führen, dass der Fehler über einen größeren Frequenzbereich "verschmiert" werden würde, ohne dass der Fehler selbst verkleinert werden könnte. Erst die Entfernung der Drift durch die Rekonstruktion der Impedanz mittels ZHIT führt zu einer signifikant besseren Übereinstimmung zwischen Messung und Modell.
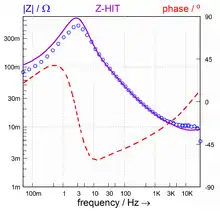
In Abbildung 4 ist das Bodediagramm einer Serien-Impedanzmessung abgebildet, das an einer Brennstoffzelle gemessen wurde, wobei absichtlich der Wasserstoff des Brenngases durch Zusatz von Kohlenmonoxid vergiftet wurde[7]. Durch die Vergiftung mit Kohlenmonoxid werden aktive Zentren des Platinkatalysators blockiert, wodurch die Leistungsfähigkeit der Brennstoffzelle stark beeinträchtigt wird. Die Blockierung des Katalysators ist dabei potentialabhängig, wobei sich in der Zelle eine abwechselnde Sorption und Desorption des Kohlenmonoxids an der Katalysatoroberfläche einstellt. Diese ("zyklische") Veränderung der aktiven Katalysatoroberfläche äußert sich in pseudoinduktiven Verhalten, das im Impedanzspektrum der Abbildung 4 bei tiefen Frequenzen (< 3 Hz) beobachtet werden kann. In dieser Abbildung wird die durch den ZHIT rekonstruierte Verlauf der Impedanz durch die violette Linie dargestellt, während die Stützstellen aus den Original Messwerten durch die blauen Kreise dargestellt sind. Man kann sehr deutlich die Abweichung im tieffrequenten Teil der Messung zwischen diesen beiden Kurven erkennen. Die Auswertung der Spektren nach einem gewählten Modell zeigt[7], dass sich deutlich bessere Übereinstimmung zwischen Modell und Messung erhalten lassen, wenn die rekonstruierten ZHIT-Impedanzen zur Berechnung der Impedanzen anstelle der Original-Messdaten herangezogen werden.
Literatur
Originalarbeiten:
- C. A. Schiller, F. Richter, E. Gülzow, N. Wagner: Validation and evaluation of electrochemical impedance spectra of systems with states that change with time. In: Physical Chemistry Chemical Physics. Band 3, Nr. 3, 1. Januar 2001, S. 374–378, doi:10.1039/B007678N.
Weiterführende Literatur:
- W. Ehm, R. Kaus, C. A. Schiller, W. Strunz: Z-HIT — A Simple Relation Between Impedance Modulus and Phase Angle. Providing a New Way to the Validation of Electrochemical Impedance Spectra. In: F. Mansfeld, F. Huet, O. R. Mattos (Hrsg.): New Trends in Electrochemical Impedance Spectroscopy and Electrochemical Noise Analysis. Electrochemical Society Inc., Pennington, NJ, 2001, vol. 2000-24, ISBN 1-56677-291-5, S. 1–10.
- Andrzej Lasia: Z-HIT Transform. In: Electrochemical Impedance Spectroscopy and its Application. Springer New York Heidelberg Dordrecht London, 2014, ISBN 978-1-4614-8932-0, S. 299.
Einzelnachweise
- W. Ehm, H. Gohr, R. Kaus, B. Roseler, C. A. Schiller: The evaluation of electrochemical impedance spectra using a modified logarithmic Hilbert transform. In: ACH-Models in Chemistry. Band 137, Nr. 2–3, 2000, S. 145–157.
- W. Ehml: Expansions for the Logarithmic Kramers—Kronig Relations. 1998 (PDF auf zahner.de [abgerufen am 29. November 2014] Unveröffentlichte Arbeit).
- Zahlenwerte Zetafunktion
- CPE(mathematisch)
- CPE(physikalisch)
- W. Strunz, C. A. Schiller, J. Vogelsang: The change of dielectric properties of barrier coatings during the initial state of immersion. In: Materials and Corrosion. Band 59, Nr. 2, 1. Februar 2008, S. 159–166, doi:10.1002/maco.200804156.
- C. A. Schiller, F. Richter, E. Gülzow, N. Wagner: Relaxation impedance as a model for the deactivation mechanism of fuel cells due to carbon monoxide poisoning. In: Physical Chemistry Chemical Physics. Band 3, Nr. 11, 1. Januar 2001, S. 2113–2116, doi:10.1039/B007674K.