Weyl-Kammer

In d​er Mathematik i​st die Weyl-Kammer (benannt n​ach Hermann Weyl) e​in Begriff a​us der Theorie d​er Lie-Gruppen. Weyl-Kammern werden b​ei der Definition positiver u​nd einfacher Wurzeln benötigt, außerdem spielen s​ie eine zentrale Rolle i​n der Theorie d​er Gebäude.

Definition

Sei ${\displaystyle {\mathfrak {g}}}$ eine endlichdimensionale halbeinfache Lie-Algebra, ${\displaystyle {\mathfrak {a}}\subset {\mathfrak {g}}}$ eine Cartan-Unteralgebra und ${\displaystyle ({\mathfrak {a}},R)}$ das zugehörige Wurzelsystem.

Für eine Wurzel ${\displaystyle \alpha \in R\subset {\mathfrak {a}}}$ bezeichne

${\displaystyle E_{\alpha }:=\left\{x\in {\mathfrak {a}}:\alpha ^{\vee }(x)=0\right\}\subset {\mathfrak {a}}}$

die zugehörige Hyperebene in ${\displaystyle {\mathfrak {a}}}$.

Dann heißen d​ie Zusammenhangskomponenten von

${\displaystyle {\mathfrak {a}}\setminus \cup _{\alpha \in R}E_{\alpha }}$

die Weyl-Kammern d​es Wurzelsystems.

Wirkung der Weyl-Gruppe

Die Weyl-Gruppe von ${\displaystyle {\mathfrak {g}}}$ wirkt auf ${\displaystyle {\mathfrak {a}}}$ und permutiert die Menge der Weyl-Kammern, d. h. die Wirkung der Weyl-Gruppe auf der Menge der Weyl-Kammern ist einfach transitiv und die Anzahl der Weyl-Kammern ist die Kardinalität der Weyl-Gruppe.

Der Abschluss einer Weyl-Kammer ist ein Fundamentalbereich für die Wirkung der Weyl-Gruppe auf ${\displaystyle {\mathfrak {a}}}$.

Weyl-Kammern in symmetrischen Räumen

Es sei ${\displaystyle X=G/K}$ ein symmetrischer Raum von nichtkompaktem Typ. Dann sind alle ${\displaystyle x}$ enthaltenden Flachs ${\displaystyle F\subset X}$ von der Form

${\displaystyle F=exp_{x}({\mathfrak {a}})}$

für eine abelsche Unteralgebra ${\displaystyle {\mathfrak {a}}\subset {\mathfrak {p}}}$. (Hier ist ${\displaystyle exp_{x}\colon {\mathfrak {p}}\to X}$ die Exponentialabbildung in ${\displaystyle x\in X}$ und ${\displaystyle {\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}}$ die Cartan-Zerlegung.)

Insbesondere lässt sich der Begriff der Weyl-Kammern auf Flachs in symmetrischen Räumen übertragen: Weyl-Kammern in ${\displaystyle F}$ sind (per Definition) die Bilder der Weyl-Kammern in ${\displaystyle {\mathfrak {a}}}$ unter der Exponentialabbildung.

Beispiel

Wurzelsystem A₂

Es sei

${\displaystyle {\mathfrak {g}}=sl(3,\mathbb {R} )=\left\{A\in \operatorname {Mat} (3,\mathbb {R} ):\operatorname {Spur} (A)=0\right\}}$

und

${\displaystyle {\mathfrak {a}}=\left\{\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}):\lambda _{1}+\lambda _{2}+\lambda _{3}=0\right\}}$.

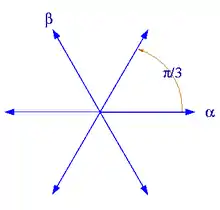
Das zugehörige Wurzelsystem besteht a​us den 6 Wurzeln

${\displaystyle \alpha _{1}=diag(1,-1,0)}$

${\displaystyle \alpha _{2}=diag(1,0,-1)}$

${\displaystyle \alpha _{3}=diag(0,1,-1)}$

${\displaystyle \alpha _{4}=diag(-1,1,0)}$

${\displaystyle \alpha _{5}=diag(-1,0,1)}$

${\displaystyle \alpha _{6}=diag(0,-1,1)}$

entsprechend

${\displaystyle \alpha _{1}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{1}-\lambda _{2}}$

${\displaystyle \alpha _{2}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{1}-\lambda _{3}}$

${\displaystyle \alpha _{3}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{2}-\lambda _{3}}$

${\displaystyle \alpha _{4}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{2}-\lambda _{1}}$

${\displaystyle \alpha _{5}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{3}-\lambda _{1}}$

${\displaystyle \alpha _{6}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{3}-\lambda _{2}}$.

Die ${\displaystyle E_{\alpha }}$'s sind drei Geraden im zweidimensionalen Vektorraum ${\displaystyle \alpha }$, sie zerlegen ${\displaystyle \alpha }$ in sechs Weyl-Kammern.

Die Weyl-Gruppe ist in diesem Fall die symmetrische Gruppe ${\displaystyle S_{3}}$, sie permutiert die sechs Weyl-Kammern.

Literatur

• Armand Borel: Linear algebraic groups. W. A. Benjamin, New York / Amsterdam 1969
• Alexander Kirillov Jr.: An introduction to Lie groups and Lie algebras. In: Cambridge Studies in Advanced Mathematics, 113. Cambridge University Press, Cambridge 2008, ISBN 978-0-521-88969-8
• Ira Gessel, Dorn Zeilberger: Random walk in a Weyl chamber. JSTOR 2159560

Weblinks

• John Dusel: Root Systems. (PDF)
• Raphaël Rouquier: Weyl groups, affine Weyl groups and reflection groups (PDF; 136 kB)
• Allen Knutson: Weyl groups and Weyl chambers
• Weyl Chamber. Planet Math