Volta-Spannung
In der Elektrochemie versteht man unter Volta-Spannung, Kontaktspannung[1] oder auch Berührungsspannung (nicht zu verwechseln mit der Berührungsspannung bei elektrischen Geräten) die Differenz der äußeren elektrischen Potentiale, die auf die Überschussladungen entgegengesetzten Vorzeichens an den Phasengrenzen zurückzuführen sind.
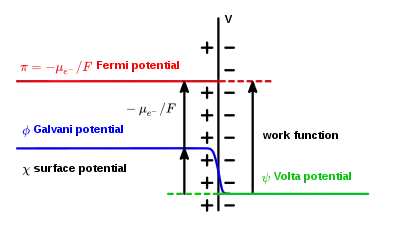
Die Volta-Spannung ist ein Phänomen der Kontaktelektrizität.
Der Name geht auf den italienischen Naturforscher und Erfinder Alessandro Volta zurück.
Zusammen mit der als Galvani-Spannung bezeichneten Differenz der inneren elektrischen Potentiale ergibt sich die gesamte Potentialdifferenz zwischen zwei Phasen. Die verschiedenen Arten der Potentialdifferenzen spielen bei der exakten Behandlung von Galvanischen Zellen eine Rolle.
Die Volta-Spannung hängt mit der Galvani-Spannung über die (elektrische) Oberflächenpotentialdifferenz zusammen[2]:
Volta-Spannung zwischen zwei Leitern

Nimmt ein Metall aus dem Vakuum ein (ruhendes) Elektron auf, so landet es in ihm auf dem Fermi-Niveau. Die frei werdende Bindungsenergie heißt Austrittsarbeit. Kommen nun zwei Leiter mit unterschiedlichen Austrittsarbeiten, die zunächst jeweils ungeladen sind (Anzahl Elektronen passend zu den Kernladungen), in elektrischen Kontakt zueinander, so fließen kurzzeitig Elektronen in Richtung des Leiters mit der höheren Austrittsarbeit (zum tieferen Fermi-Niveau), bis im thermodynamischen Gleichgewicht die Fermi-Niveaus angeglichen sind. Erklärung für den Angleich: Die Nettoladung verteilt sich ‘in’ der Oberfläche der Leiter, durch Influenz bevorzugt dort, wo die Oberflächen sich nahe sind. Sowohl in der (bei Metallen sehr dünnen) Raumladungszone als auch im Außenraum entsteht ein elektrisches Feld, das dem weiteren Stromfluss entgegenwirkt – quantitativ: Das Wegintegral der Feldstärke vom Inneren des einen Leiters ins Innere des anderen, das sogenannte „Kontaktpotential“, ist gleich der Differenz der Austrittsarbeiten. (Eigentlich handelt es sich beim „Kontaktpotential“ um eine Potentialdifferenz, also eine Spannung, aber die Bezeichnung Kontaktspannung hat auch eine andere Bedeutung, siehe Kontaktwiderstand).
Das elektrische Feld im Außenraum macht sich z. B. bei Elektronenröhren bemerkbar, deren Gitter mit der Kathode kurzgeschlossen ist: Von der Kathode thermisch emittierte Elektronen werden durch dieses Feld wieder auf die Kathode zurückgetrieben. Wird das Gitter durch eine externe Spannung positiver gemacht, so steigt der Anodenstrom an, bis diese Spannung das Kontaktpotential gerade ausgleicht und das äußere Feld verschwindet.[3] Störender ist das Außenfeld in Elektronenoptiken für niederenergetische Elektronen und in Präzisionsexperimenten wie Gravity Probe B. Die Variation der Austrittsarbeit entsteht dabei durch Verunreinigungen der Oberflächen.
Werden die elektrischen Leiter getrennt, so fließen mit der Verringerung der Kontaktfläche die Ladungen zum größten Teil zurück. Die verbleibende Ladungsmenge hängt davon ab, wie dicht sich große Flächen der Leiter gegenüberstehen in genau jenem Moment, wenn der letzte leitende Kontakt abreißt, denn bis dahin bleibt die Spannung konstant, während die Feldstärke mit zunehmendem Abstand sinkt. Dielektrische Schichten, z. B. oxidiertes Metall, über einem Großteil der Oberfläche können die Ladungsmenge erhöhen, nicht nur durch ihre relative Permittivität, sondern vor allem indem sie einen engen mechanischen Kontakt ohne gleichzeitigen elektrischen Kontakt erlauben. Nach der endgültigen Trennung bleiben Ladung und Feldstärke konstant (bis auf Umverteilungen), sodass die Spannung proportional zum Abstand ansteigt (bis der Abstand größer wird als die Ausdehnung der Körper).
In einem Stromkreis wird durch das oben geschilderte Kontaktpotential normalerweise kein Strom fließen (da die Kontaktspannung im Gleichgewicht vorliegt). Insbesondere misst man keine Spannung, wenn man die beiden verschiedenen Leiter jeweils mit einer der beiden Prüfspitzen eines Messgerätes verbindet, denn die beiden zusätzlichen Kontaktstellen unterscheiden sich um die gleiche Austrittsarbeitsdifferenz wie der ursprüngliche Kontakt. Allerdings ist das Fermi-Niveau und damit die Austrittsarbeit temperaturabhängig, bei manchen Materialien durch eine Asymmetrie der Zustandsdichte sogar stark. Dadurch entsteht in einer ABA-Anordnung zweier Materialien A und B mit unterschiedlich temperierten Kontaktstellen AB bzw. BA eine Thermospannung (Seebeck-Effekt) bzw. bei Kurzschluss ein Thermostrom.
Eine andere Ursache für einen anhaltenden Stromfluss und damit leicht messbare Effekte sind elektrochemische Reaktionen. Das komplizierte Zusammenspiel von elektrischen, elektrochemischen und Membranpotentialen wurde von Galvani, Volta und Humboldt erkundet und unterschiedlich interpretiert.[4]
Literatur
- Gerd Wedler: Lehrbuch der Physikalischen Chemie (VCH, Weinheim, 1987), ISBN 3-527-26702-6.
- Eintrag zu contact potential difference (Volta potential difference). In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.C01293 – Version: 2.3.3.
Einzelnachweise
- https://www.spektrum.de/lexikon/chemie/kontaktspannung/5036
- Herbert Herman: Treatise on Materials Science and Technology: Materials Science Series, Vol. 1. Elsevier, 2013, ISBN 978-1-4832-1810-6, S. 26 (google.de).
- H. Barkhausen: Lehrbuch der Elektronenröhren. 1. Band Allgemeine Grundlagen. 11. Auflage. S. Hirzel Verlag, 1965, S. 41 (Kap. 4 Anlaufstrom).
- Oliver Lodge: On the Controversy Concerning Volta's Contact Force, Kessinger Publishing, 2005, ISBN 978-1-4179-7464-1, eingeschränkte Vorschau in der Google-Buchsuche.