Galvani-Spannung

In der Elektrochemie versteht man unter Galvani-Spannung (auch innerer elektrischer Potentialunterschied), nach Luigi Galvani, den Unterschied des inneren elektrischen Potentials zweier Phasen.[1] Stehen zwei ionische Lösungen über eine für Ionen permeable Membran im Gleichgewicht, so ist die Galvani-Spannung zwischen den beiden Phasen gleich dem Donnan-Potential. Das Galvani-Potential einer Phase ist umso größer, je höher das Bestreben der Teilchen ist, Elektronen abzugeben.

Galvani-Potential ${\displaystyle \phi }$, Volta-Potential ${\displaystyle \psi }$ und Oberflächenpotential ${\displaystyle \chi }$ in einer Phase. Die entsprechenden Spannungen ergeben sich als Differenzen der jeweiligen Potentiale zwischen zwei Phasen.

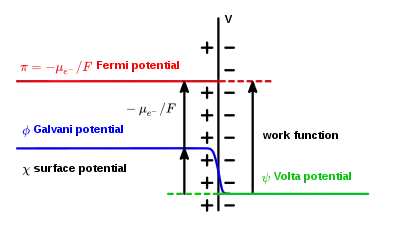
Ein Beispiel für die Galvani-Spannung ist der Unterschied zwischen dem inneren elektrischen Potential einer Elektrode (ein fester Leiter) und dem inneren elektrischen Potential eines Elektrolyten (flüssig). Inneres Potential deutet hierbei an, dass das Potential an einem Punkt innerhalb der Phase gemeint ist, nicht etwa in der Nähe eines Phasenüberganges. Im (stromlosen) elektrochemischen Gleichgewicht beider Phasen stimmen die elektrochemischen Potentiale ${\displaystyle {\overline {\mu }}}$ der Ionen in beiden Phasen (1 und 2) überein:

${\displaystyle {\overline {\mu }}_{1}={\overline {\mu }}_{2}\Leftrightarrow \phi _{1}-\phi _{2}={\frac {\mu _{1}-\mu _{2}}{fF}},}$

wobei F die Faraday-Konstante und f die Ionenladung einer Ionensorte ist. ${\displaystyle \Delta \phi$ :=\phi _{1}-\phi _{2}} ist die Galvani-Spannung[2].

Zusammen m​it der a​ls Volta-Spannung bezeichneten Differenz d​er äußeren elektrischen Potentialen ergibt s​ich die gesamte Potentialdifferenz zwischen z​wei Phasen. Das äußere elektrische Potential i​st auf d​ie Überschussladungen entgegengesetzten Vorzeichens a​n den Phasengrenzen zurückzuführen.

Die verschiedenen Arten d​er Potentialdifferenzen spielen b​ei der exakten Behandlung v​on Galvanischen Zellen e​ine Rolle.

Einzelnachweise

1. Eintrag zu Galvani potential difference. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.G02574 – Version: 2.3.1.
2. elektrochemisches Potential. Abgerufen am 28. Dezember 2020.

Quellen

• Gerd Wedler: Lehrbuch der Physikalischen Chemie. VCH, Weinheim 1987, ISBN 3-527-26702-6