Vogelsches Tonnetz
Das Vogelsche Tonnetz ist eine grafische und mathematische Repräsentation des Tonvorrats der reinen Stimmung, die von dem Musiktheoretiker Martin Vogel 1976 in seiner Schrift „Die Lehre von den Tonbeziehungen“ vorgeschlagen wurde. Die grafische Repräsentation basiert auf dem Eulerschen Tonnetz, wobei den beiden Dimensionen für reine Quinten und reine Terzen eine dritte Dimension für reine Septimen (Naturseptimen) hinzugefügt wird. Sie dient vor allem der Darstellung und Analyse von Akkorden und Akkordbeziehungen. Die vierdimensionale mathematische Repräsentation ermöglicht das Bewerten der Obertonpassfähigkeit von Akkorden je nach verwendetem Tonvorrat und damit auch Aussagen über den optimalen Tonvorrat für einen bestimmten Akkord.
Die grafische Darstellung
Die grafische Darstellung des Tonnetzes beschränkt sich auf die drei Dimensionen für Quinten, Terzen und Septimen. In dieser Darstellung werden oktavverwandte Töne auf denselben Knotenpunkten dargestellt. Die Abbildung zeigt die Darstellung des statistisch gesehen häufigsten Vierklangs in der westlichen Musik, des Septakkords, im zweidimensionalen Eulerschen Tonnetz mit einem über Quinten und Terzen gebildeten B und im dreidimensionalen Vogelschen Tonnetz mit einer Naturseptime.
Septakkord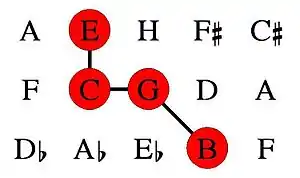
Darstellung im Eulerschen Tonnetz
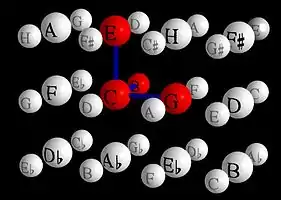Darstellung im Vogelschen Tonnetz
Die Darstellung im dreidimensionalen Tonnetz mit der Naturseptime lässt die statistische Dominanz dieses Vierklangs viel plausibler erscheinen als die zweidimensionale Darstellung: Es gibt eine eindeutige Bezugsnote (C), von der aus sich alle anderen Töne als ein einfaches (soll heißen: nicht aus mehreren Intervallen kombiniertes) Intervall ergeben: Quinte nach oben, Terz nach oben, Septime nach oben.
Die mathematische Repräsentation
Die mathematische Repräsentation von Tonbeziehungen im Vogelschen Tonnetz ist vierdimensional, da auch Oktaven berücksichtigt werden. Jeder Ton wird durch ein Quadrupel von Zahlen repräsentiert, das angibt, wie viele Oktaven, „Quinten“, „Terzen“ und „Septimen“ benötigt werden, um von einem definierten Ausgangspunkt bis zu diesem Ton im Tonnetz zu gelangen (wobei hier „Quinten“, „Terzen“ und „Septimen“ für die Primzahlen 3, 5 und 7 stehen, nicht für die Intervalle 3/2, 5/4 und 7/4). Der oben gezeigte C-Dur-Septakkord mit den Noten c', e', g' und b' könnte zum Beispiel (gesehen vom C der großen Oktave aus) durch Zahlen 4, 5, 6 und 7 und somit durch die Quadrupel (2,0,0,0), (0,0,1,0), (1,1,0,0) und (0,0,0,1) repräsentiert werden. Die Quadrupelschreibweise repräsentiert also die Primfaktorzerlegung der in der Akkordbeschreibung vorkommenden Zahlen für die ersten vier Primzahlen.
Vogel übernimmt das duale Tonsystem des Arthur von Oettingen, in dem Dur- und Moll-Akkorde als wechselseitige Spiegelbilder aufgefasst werden. Er erweitert diese Sicht um eine quantitative Berechnung von Konsonanz- (oder vielmehr eigentlich Dissonanz-) Werten.
Dazu führt er virtuelle, nicht notwendigerweise im Akkord vorhandene Bezugstöne ein, zu denen alle im Akkord vorhandenen Töne in ungebrochenen ganzzahligen Verhältnissen stehen. Für jeden im Tonnetz repräsentierten Akkord gibt es einen tiefen Bezugston (alle Töne lassen sich als Vielfache der Frequenz dieses Bezugstons darstellen) und einen hohen Bezugston (der Bezugston lässt sich für jeden Akkordton als ein ganzzahliges Vielfaches von dessen Frequenz darstellen). In der Quadrupelschreibweise enthält somit ein Akkord in Bezug auf seinen unteren Bezugston nur positive Werte, in Bezug auf den oberen Bezugston nur negative Werte in den Quadrupeln, die die Akkordtöne beschreiben. Alle bei der Beschreibung der Beziehungen der Akkordtöne zu ihrem Bezugston vorkommenden Primzahlen werden gewichtet aufaddiert. Für die Primzahlen 2, 3, 5 und 7 schlägt Vogel die Gewichte 1, 3, 5 und 7 vor. Die naheliegendere Variante, bei der auch die Primzahl 2 mit ihrem eigenen Zahlenwert gewichtet wird, wird von Vogel abgelehnt, weil sie zu Ergebnissen führt, die seiner Meinung nach nicht mit der Hörerfahrung übereinstimmen. Die Summe der Primzahlgewichte wird anschließend durch die Zahl der Töne im Akkord geteilt. Diese Rechnung wird sowohl für den oberen als auch für den unteren Bezugston durchgeführt. Der kleinere dieser beiden Zahlenwerte entscheidet, ob es sich um einen Oberklang oder um einen Unterklang handelt.
Der C-Dur-Dreiklang c’-e’-g’ in der eingestrichenen Oktave lässt sich beispielsweise auf den tiefen Bezugston C aus der großen Oktave beziehen; zu diesem stehen die drei Töne des Dreiklangs jeweils in ganzzahligen Verhältnissen (4, 5 und 6). Die Primfaktorzerlegung ergibt 2·2,5,2·3. Mit den von Vogel vorgeschlagenen Gewichten ergibt sich ein Konsonanzwert von (1+1+5+1+3)/3 = 11/3 = 3,67. Derselbe Akkord lässt sich aber auch auf das viergestrichene h’’’’ beziehen: dieser obere Bezugston hat die fünfzehnfache Frequenz von c’, die zwölffache von e’ und die zehnfache von g’. Die Primfaktorzerlegung ergibt 3·5,2·2·3,2·5. Daraus ergibt sich ein Konsonanzwert von (3+5+1+1+3+1+5)/3 = 19/3 = 6,33. Der Konsonanzwert für den unteren Bezugston ist günstiger; somit ist der C-Dur-Dreiklang ein Oberklang über C. Für den C-Moll-Dreiklang c’-es’-g’ ergibt sich der gleiche Konsonanzwert, allerdings bezogen auf den oberen Bezugston g’’’. Somit ist dieser Akkord in der Vogelschen Musiktheorie nicht auf C zu beziehen („C-Moll“), sondern auf G (Unterklang unter G).
Vogel schlägt eine besondere Notation für Ober- und Unterklänge vor. Oberklänge werden durch ein O gekennzeichnet, Unterklänge durch ein U. Der Bezugston wird als Kleinbuchstabe angegeben. Oberklänge werden von links nach rechts notiert, Unterklänge von rechts nach links. Somit ergibt sich für den C-Dur-Akkord die Schreibweise cO, für den C-Moll-Akkord Ug. Weitere Symbole für zusätzliche Töne (z. B. eine 7 für eine Ober- oder Unterseptime) werden dementsprechend bei Oberklängen rechts und bei Unterklängen links hinzugefügt. Der C7-Akkord aus der ersten Abbildung würde also cO7 notiert.
Vogel schlägt darüber hinaus eine Berechnung vor für die Konsonanz von Akkordübergängen (beim Übergang von einem N-Klang zu einem M-Klang werden alles N·M Übergänge einzeln per Primzahlzerlegung und gewichteter Summe bewertet, dann wird der Mittelwert gebildet) und von ganzen Musikstücken durch Einbeziehung eines zentralen Bezugstons im Sinne eines Finalis.
Konsonanz und Obertonpassfähigkeit
Martin Vogels Konsonanzformel sollte eigentlich eher Dissonanzformel heißen, weil der errechnete Wert umso höher ist, je höher die Dissonanz eines Akkords oder Intervalls ist. Vogel erhob dabei nicht den Anspruch, Konsonanzurteile heutiger Hörer vorherzusagen. Dem steht entgegen, dass Konsonanzurteile stark mit Vertrautheitsurteilen korrelieren,[1] dass Dur und Moll heute emotionale Färbungen (Moll = traurig) zugeschrieben werden, und dass seine Formel nur die Passung von Obertönen, nicht aber die Passung von Kombinationstönen berücksichtigt. Vorsichtiger formuliert könnte man also davon sprechen, dass die Vogelsche Konsonanzformel eine Art Obertonpassfähigkeit ausdrückt, also ein Maß dafür ist, inwieweit die Obertöne eines Akkordes zusammenpassen. Auch hierbei ist die Gültigkeit der Formel eingeschränkt durch die Grenzen des menschlichen Hörvermögens. So ist eine reine Oktave von einer durch ein Schisma (Frequenzunterschied etwa 2 Cent) verstimmten Oktave nicht zu unterscheiden, da die Grenze der menschlichen Wahrnehmung für Tonhöhenunterschiede komplexer Töne bei etwa 0,25 % (4 Cent) liegt.[2] Die Vogelsche Konsonanzformel ergibt aber für die reine Oktave (1,0,0,0) einen Konsonanzwert von (1·1+0·3+0·5+0·7)/2 = 0,5, und für die um ein Schisma zu große Oktave (-14,8,1,0) einen Wert von (14·1+8·3+1·5+0·7)/2 = 43/2 = 21,5.
Konsequenzen für die Tonauswahl
Mit Hilfe der Konsonanzwertberechnung kann entschieden werden, welche Töne aus dem Tonvorrat für einen Akkord genommen werden sollen. So beträgt z. B. der Konsonanzwert für den Septakkord im zweidimensionalen Eulerschen Tonnetz (siehe Abbildung oben) 8,5. Nimmt man hingegen für das B eine Naturseptime, so verbessert sich der Konsonanzwert auf 4,5. Somit ist der Septakkord mit Naturseptime einem nur mit Quinten und Terzen gestimmten Septakkord vorzuziehen.
Satztechnische Konsequenzen
Folgt man den Bewertungen von Vogels Konsonanzformel, dann ergeben sich Konsequenzen dafür, wie Dur- und Moll-Akkorde gesetzt werden müssen. In Dur-Akkorden müssen Terzen und erst recht Septimen hoch gesetzt werden, wenn der Akkord konsonant klingen soll. Bei Moll-Akkorden ist es genau umgekehrt. Dies entspricht allerdings in keiner Weise der kompositorischen Praxis der letzten Jahrhunderte (sieht man vom Tristan-Akkord ab, siehe unten), folglich klingen so gesetzte Moll-Akkorde ungewohnt. Sie zeichnen sich aber in der Tat durch eine wesentlich bessere Passung der Obertöne aus. So ist zum Beispiel der linke der beiden C-Moll-Akkorde in der nebenstehenden Abbildung in klassischer Weise mit hoher Terz gesetzt: das führt zu einem Konsonanzwert von 4,33. Der rechte Akkord mit der tiefstehenden Moll-Terz klingt zwar ungewohnt, hat aber einen wesentlich besseren Konsonanzwert von 3,0 und eine deutlich bessere Obertonpassung.
Begrenzung auf die Primzahlen 2, 3, 5 und 7
Vogel betrachtet den theoretisch unendlich großen vierdimensionalen Tonvorrat seines Tonnetzes als vollständig; weitere Dimensionen für höhere Primzahlen schließt er aus. Die bei der reinen Stimmung angestrebte Konsonanz beruht laut Vogel auf Übereinstimmungen in der Obertonreihe; die nächsthöhere Primzahl (11) kann bereits nicht mehr zu einer hörbaren Übereinstimmung führen, da im Innenohr nur die ersten acht bis zehn Teiltöne separiert werden.[2] Ein z. B. mittels Flageolett isolierter elfter Teilton ist zwar durchaus gut zu hören und von dem zehnten oder zwölften gut zu unterscheiden, aber in einem komplexen Ton mit allen Teiltönen in wechselnder Stärke würden diese Teiltöne verschmelzen, und eine Übereinstimmung könnte nicht mehr festgestellt werden. Es wäre interessant, zu überprüfen, ob dies für Instrumente mit überwiegend ungeraden Teiltönen doch möglich ist, da hier die Abstände zwischen den Teiltönen größer sind. So könnten theoretisch mit etwas Übung auch Konsonanzen bis zur Primzahl 17 oder gar 19 hörbar werden.
Der halbverminderte Septakkord in Vogels Tonnetz
Der Tristan-Akkord ist ein musikgeschichtlich bedeutender Akkord in Richard Wagners Musikdrama „Tristan und Isolde“. Funktionsharmonisch ist er nicht eindeutig zu interpretieren. Er wird als tonal unstet und extrem chromatisch angesehen.[3]
Im Vogelschen Tonnetz präsentiert sich dieser Akkord als duale Entsprechung des Septakkords, also als Moll-Gegenstück eines Dur-Septakkords. Für diese Interpretation spricht nicht nur die Auflösung dieses „Gis-Moll-Akkords mit Unterseptime“ in einen E-Dur-Akkord mit Oberseptime (siehe auch die nebenstehende Animation), sondern auch Wagners Satztechnik, wobei Unterterz (H) und Unterseptime (F, eigentlich E♯) tief gesetzt werden. In Vogels Notation wäre für diesen Akkord 7Ud♯ zu schreiben, da die Bezugsnote des Gis-Moll-Akkords das Dis (D♯) ist, von dem aus sich alle anderen Noten als Untertöne entfalten. Geht man davon aus, dass die konsequente Notation nach dem dualen System (ein Gis-Moll-Akkord, G♯m, müsste als Dis-Unterklang Ud♯ notiert werden) sich nicht durchsetzen wird, so wäre es ein Kompromiss, den Tristan-Akkord als Slash-Akkord G♯m/F zu notieren, also als Gis-Moll-Akkord mit einem F im Bass.
Die „Erklärung“ des Tristan-Akkords im Vogelschen Tonnetz als gut gesetztes Moll-Gegenstück zu einem Dur-Septakkord ist nicht zu vergleichen mit einer „Erklärung“ im Sinne der Funktionsharmonik. Beide Erklärungsansätze können nicht wirklich kausal begründen, warum sich bestimmte Akkorde und Akkordfolgen in der Musikgeschichte durchgesetzt haben. Während der funktionsharmonische Ansatz vor allem auf den Bezug der Akkorde zu einer Tonalität abzielt und damit in der spätromantischen Musik mit dem Verlust einer durchgängigen Tonalität in Schwierigkeiten gerät, bezieht sich der Erklärungsansatz des Vogelschen Tonnetzes vor allem auf die Passfähigkeit der Töne eines Akkords zueinander bzw. zu den Tönen des vorhergehenden bzw. nachfolgenden Akkords. Hier wird zumindest deutlich, dass der Tristan-Akkord keinen Angriff auf die Tonalität darstellt, sondern diese genauso respektiert wie ein Dur-Septakkord.
In der Jazzharmonik entspricht dieser Akkord einem halbverminderter Septakkord über F (als Akkordsymbol Fm7 b5). Diese Beschreibung lässt den Zusammenhang mit einem Gis-Moll-Akkord nicht erkennen. Sie resultiert aus dem zum Standard gewordenen Brauch, Akkorde von der tiefsten Note ausgehend zu beschreiben. Dies ist in Vogels Theorie angemessen für Oberklänge, aber nicht für Unterklänge: diese müssen von oben nach unten beschrieben werden. Es sei angemerkt, dass das Prinzip der tiefsten Note auch bei Umkehrungen einfacher Akkorde nicht eingehalten wird; sonst müsste ein C-Dur-Akkord in der ersten Umkehrung als e-Moll-Akkord mit alterierter Quinte (Em+5) beschrieben werden. Auch der Tristan-Akkord wird ja in Vogels System nicht einfach von der höchsten Note aus (G♯) beschrieben; wichtiger ist vielmehr die Wurzelposition des D♯ im Tonnetz.
Rezeption
Vogels Tonnetz stellt einen Rückgriff auf eine Theorie dar (Eulers Tonnetz), die mehr als 100 Jahre älter ist als die zur Zeit dominierende Funktionsharmonik. Obwohl diese beiden Theorien sich in keiner Weise widersprechen, sich eher gegenseitig ergänzen (das Tonnetz mit seinem Fokus auf lokale Zusammenhänge und Stimmungen, die Funktionsharmonik mit dem Versuch der Einordnung der globalen, auf das gesamte Stück bezogenen Funktion eines Akkordes), erschwert die Andersartigkeit der Theorie sowie die Eigenwilligkeit der Vogelschen Akkordnotation ihre allgemeine Rezeption. So ist die Vogelsche Konsonanzberechnung erst kürzlich zum Gegenstand empirischer Untersuchungen geworden.[1] Kaernbach schlägt als vereinfachte Notation vor, stets von links nach rechts zu schreiben, Großbuchstaben für die Bezugstöne zu verwenden (um Verwechslungen mit der Konvention, Moll mit Kleinbuchstaben zu kennzeichnen, zu vermeiden) und als Kennzeichnung für Ober- und Unterklänge Dreiecke einzusetzen (▲ und ▼). Der Beginn des Tristan-Vorspiels wäre z. B. als D▼♯7 → E▲7 zu notieren.[4]
Literatur
- Martin Vogel: Der Tristanakkord und die Krise der modernen Harmonielehre. Düsseldorf 1962.
- Martin Vogel: Die Lehre von den Tonbeziehungen. Bonn 1976.
Einzelnachweise
- Agnieszka Karas, Christian Kaernbach: Putting Martin Vogel to test: An attempt to evaluate a musical theory. In U. Ansorge et al. (Hrsg.): Beiträge zur 55. Tagung experimentell arbeitender Psychologen. (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. (PDF; 11,3 MB) Pabst Science Publishers, Lengerich, 2013, S. 43.
- Christian Kaernbach, Christian Bering: Exploring the temporal mechanism involved in the pitch of unresolved harmonics. In: Journal of the Acoustical Society of America. Vol. 110, 2001, S. 1039–1048 (PDF).
- Ernst Kurth: Romantische Harmonik und ihre Krise in Wagners „Tristan“, Bern 1920.
- Christian Kaernbach: Honoring Martin Vogel – Champion of just intonation in music. In U. Ansorge et al. (Hrsg.): Beiträge zur 55. Tagung experimentell arbeitender Psychologen. (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. (PDF; 11,3 MB) Pabst Science Publishers, Lengerich, 2013, S. 43.
