Treynor-Quotient

Der Treynor-Quotient, auch das Treynor-Maß oder das Treynor-Verhältnis genannt (englisch Treynor ratio), ist eine betriebswirtschaftliche Kennzahl, die das Verhältnis der Überschussrendite zum Betafaktor und somit die Risikoprämie je Einheit des eingegangenen systematischen Risikos bemisst.[1] Die Kennzahl wurde von Jack Treynor 1965 im Rahmen von Arbeiten zum Kapitalgutpreismodell (CAPM) vorgestellt.

Formale Darstellung

Anlagen über bzw. unter der Wertpapierlinie sind überbewertet bzw. unterbewertet.

Die Kennzahl leitet sich aus der zentralen Gleichung des CAPM her, der Wertpapierlinie:

E[R_{i}]=r_{f}+\beta _{i}(E[R_{M}]-r_{f})

.

Im Finanzmarktgleichgewicht passt sich der gegenwärtige Preis eines Wertpapiers derart an, dass die erwartete Rendite die risikolose Verzinsung um eine Risikoprämie übersteigt, die proportional mit dem Wertpapier-Betafaktor ansteigt. Diese Gleichung wird umgeformt und es ergibt sich:

T_{i}\equiv E[R_{M}]-r_{f}={\frac {E[R_{i}]-r_{f}}{\beta _{i}}}

wobei $R_{i}$ die Rendite des Portfolios, $r_{f}$ die Rendite der risikofreien Kapitalanlage und $\beta _{i}$ das Beta des Portfolios darstellt. Der Treynor-Quotient ist somit ein Maß für die erzielte Überschussrendite pro übernommener Einheit an nicht diversifizierbarem Risiko. Das Marktportfolio besitzt definitionsgemäß ein Beta von 1 und demnach ergibt sich der Treynor-Quotient direkt als Überschussrendite.

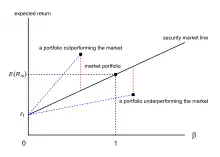
In der nebenstehenden Abbildung sind zwei Wertpapiere außerhalb der Wertpapierlinie eingezeichnet. Der jeweilige Treynor-Quotient ${\frac {E[R_{i}]-r_{f}}{\beta _{i}}}$ entspricht der Steigung einer Linie durch diese Punkte (vgl. blaue gestrichelte Linien). Eine solche Gerade gibt alle $\mu$ - $\beta$ -Kombinationen wieder, die Investoren durch Anlage in das Wertpapier zum risikolosen Zins realisieren können. Stehen zwei Portfolios unter gleichen Rahmenbedingungen zur Auswahl, so erzielt das Portfolio mit dem größeren Treynor-Quotienten seine Rendite mit geringerem systematischen Risiko. Anders formuliert würde man zwischen zwei Portfolios mit identischem Betafaktor dasjenige wählen, dass die größere Überschussrendite erzielt.

Bewertung

Im Gegensatz zum Treynor-Quotienten benutzt der Sharpe-Quotient die Standardabweichung $\sigma _{i}$ (Volatilität) statt des Betafaktors und misst somit das Gesamtrisiko, also neben dem systematischen Risiko auch das unsystematische Risiko, das aus mangelhafter Diversifizierung des Portfolios erwächst.

Vergleicht man zwei Portfolios, welche nicht aus Titeln desselben Markts bestehen, eignet sich der Sharpe-Quotient besser, da der Betafaktor des Treynor-Quotienten die Schwankungssensitivität eines Portfolios zum jeweiligen Markt ausdrückt. Der Sharpe-Quotient kann marktübergreifend angewendet werden, da die Berechnung über die Standardabweichung erfolgt.

Da es sich bei Treynor-Quotient und Sharpe-Quotient um relative Risikomaße handelt, können beide für ein Ranking von Portfolios mit einem unterschiedlichen systematischen Risiko genutzt werden.[2] Ein absolutes Beurteilungsmaß der Performance ist das Jensen-Alpha.

Die Beschaffung der für den Treynor-Quotienten erforderlichen Betawerte ist oft problematisch. Aufgrund der schlechten Datenqualität ist eine solche Berechnung bei Hedgefonds sehr kompliziert.[3] Das Treynor-Maß ist insgesamt der Kritik des CAPM unterworfen und auf dessen Prämissen angewiesen.[4]

Literatur

Jack L. Treynor: How to Rate Management of Investment Funds. In: Harvard Business Review. Band 43, Nr. 1, 1965, S. 63–75.
Klaus Spremann: Portfoliomanagement. De Oldenbourg Gruyter, 2008, ISBN 978-3-486-58779-1. Insbesondere Kapitel 11.2.3 auf S. 356ff.
Marco Wilkens, Hendrik Scholz: Von der Treynor-Ratio zur Market Risk-Adjusted Performance. In: Finanz-Betrieb. 1999, S. 308–315 (bei uni-augsburg.de [PDF; 170 kB]).

Einzelnachweise

Trautmann, Siegfried. Investitionen: Bewertung, Auswahl und Risikomanagement. Springer-Verlag, 2007. S. 178.
Bernd R. Fischer: Performanceanalyse in der Praxis: Performancemaße, Attributionsanalyse, Global Investment Performance Standards. Walter de Gruyter, 2010, S. 454–455.
Dieter G. Kaiser: Hedgefonds: Entmystifizierung einer Anlageklasse; Strukturen, Chancen, Risiken. Springer-Verlag, 2004, S. 184.
André Rutkis: Hedge-Fonds als Alternative Investments. Stilrichtungen, Risiken, Performance. Frankfurt School Verlag, Frankfurt am Main 2002, S. 72.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Trautmann, Siegfried. Investitionen: Bewertung, Auswahl und Risikomanagement. Springer-Verlag, 2007. S. 178.

[2] Bernd R. Fischer: Performanceanalyse in der Praxis: Performancemaße, Attributionsanalyse, Global Investment Performance Standards. Walter de Gruyter, 2010, S. 454–455.

[3] Dieter G. Kaiser: Hedgefonds: Entmystifizierung einer Anlageklasse; Strukturen, Chancen, Risiken. Springer-Verlag, 2004, S. 184.

[4] André Rutkis: Hedge-Fonds als Alternative Investments. Stilrichtungen, Risiken, Performance. Frankfurt School Verlag, Frankfurt am Main 2002, S. 72.